0 引言

    随着无人机技术的不断完善，无人机的应用越来越广泛。如何使无人机在规划的某片区域中寻找出一条从起始点到目标点既安全又满足相应约束条件且所花费代价最小的航迹一直是研究的热点^[1]。标准解决航迹规划问题的顺序是按照预先选定好的航迹代价函数，通过一定的搜索算法，选出总的代价函数值最小的路线作为规划出的航迹^[2-3]。

    在路径规划中，常用的搜索算法有A*算法、动态规划法、Dijkstra算法、遗传算法等。在这些算法中，由于A*算法计算简单，算法实现容易且在理论上能够保证规划出的路径全局最优，因此得到广泛应用^[3]。但是把A*算法应用在航迹规划中搜索空间将急剧增加，由此导致收敛时间变长，所需内存空间增加。针对这个问题，本文提出把无人机的机动限制结合到搜索空间中从而缩小搜索空间，同时对A*算法中的open表的管理进行改进，以提高收敛时间，缩小内存使用量。

1 改进A*算法实现航迹规划

    航迹规划的本质是在规划的区域内，在给定的约束条件下寻找一条从起点到目标点的最优或次优的飞行航迹。传统的规划算法是基于预先确定的航迹代价函数生成一条具有最小代价的航迹^[4-5]。然而，在许多应用中，这样得到的最小代价的航迹并不能满足实际需求。在实际应用中，航迹规划需考虑无人机的机动性能、碰撞概率、飞行时间等约束条件，同时由于无人机航迹规划的地域广阔，因此形成的搜索空间大。通常的搜索算法要获得一条最优航迹需要很长的收敛时间和极大的内存空间，所以在实际应用中需对搜索算法进行相应的改进。由于A*算法计算速度快、实现容易且能达到全局最优的特点，因此选择对A*算法进行改进，使其适用于无人机航迹规划。

1.1 改进A*算法

    无人机由于受机动性能、最小飞行距离、航迹距离、飞行高度等的约束，通过A*规划出来的航迹不一定能够满足无人机的实际飞行条件。在扩展节点时通常把相关的约束条件结合到搜索算法中，这样既有效减少了搜索空间，也缩短了规划所需的时间。无人机飞行时为达到最佳状态一般需要满足的约束条件有：最小飞行距离、最大拐弯角、最大爬升/下滑角、最长飞行距离、最低离地高度^[6]。

    假设给定了起始点和目标位置，一条从起始位置到当前节点的航迹，最小航迹段长度为L，最大拐弯角为φ，最大爬升/下滑角为θ，则从当前位置在最小飞行距离、最大拐弯角以及最大爬升/下滑角的约束条件下能够到达的就只有有限的位置空间。如图1所示，节点o处的纵向的张角为2θ₂，在水平面上的张角为2θ₁，扇面的半径为最小飞行距离。

    图1是未经离散化的可搜索空间示意图。在离散规划空间时，栅格的边长长度为无人机的最小飞行距离。把规划空间离散化后结合无人机的约束条件可缩小算法搜索空间。无人机飞行是有方向性的，在进行当前节点扩展时，飞行反方向的节点以及垂直于该飞行方向的邻接节点都可以裁剪掉。这样在水平方向上的最大拐弯角就可以限制在3个搜索空间中，垂直方向上的最大爬升/下滑角也同样可以限制在3个搜索空间中，这样把扩展当前节点的后继节点的搜索空间缩小为9个。如图2所示，B节点是当前新扩展节点，A点是B点的父亲节点，C点为新扩展节点的邻接计算节点。

    在三维空间中，每个栅格都是一个立方体，在水平剖面和竖直剖面上都要满足最小步长、最大拐弯角和最大爬升/下滑角。但是在实际控制中，最大转弯角和最大爬升/下滑角可以通过一定的关系转换，转化为其他直接控制的参数来满足要求。下面就分别对水平面和竖直平面进行转换。

1.1.1 水平面关系转化

    假设无人机当前节点的坐标为(x，y，z)，新扩展的节点坐标为(x₁，y₁，z₁)，航迹偏角为θ，航迹倾斜角为β，转弯半径为R，最大侧向过载为N_ymax，S₁、S₂分别为水平面上两节点的扩展步长。三维航迹规划是基于地球坐标系，水平方向是通过改变航向来躲避障碍物，因此在水平方向上的转化关系如图3所示。

    根据图3的几何关系可知新扩展的节点坐标为：

1.1.2 纵向关系转化

    无人机的纵向机动性能主要受到最大爬升/下滑角的限制。在低空飞行时，可以通过对地形坡度的限制来达到对最大爬升角的限制。

    如图4所示，假设当前节点的空间坐标为(x_i，y_i，z_i)，待扩展节点的空间坐标为(x_i+1，y_i+1，z_i+1)，两节点之间的距离为l，其爬升角为β，则由几何关系可知：

1.1.3 对open表结构进行改进

    由于在进行节点扩展寻找最优航迹时频繁地对open表中的节点执行插入、删除、排序操作，同时open表中的节点数目也相对较多，每次执行插入、删除操作后都需要对open表进行排序。顺序存储结构执行插入、删除、排序操作均较费时。执行插入、删除操作的时间复杂度是O(n)，排序的时间复杂度为O(n²)。由于在搜索时从open表中删除的是代价值最小的节点，而open表是按照节点代价值大小来组成的有序表，因此实际在执行删除操作时的时间复杂度是O(1)，当有新节点插入时即需对open表进行排序以保证open表一直处于有序状态。由此分析得出对open表的管理主要时间花销是在节点排序上，为提高整体的运行效率，这里对open表的数据结构进行一定的改进，通过采用树形的数据结构来管理open表。最小二叉堆是一种典型的树形数据结构，通过最小二叉堆对节点进行排序的时间复杂度为O(n log₂ n)，通过此种数据结构可减少open表节点排序的时间花销。

1.2 代价函数的建立

    军用无人机航迹规划的目标是在满足无人机物理特性约束以及具体飞行任务约束的前提下生成超低空地形跟随、地形回避以及威胁回避的飞行轨迹，以提高无人机的生存概率。其数学表达式为：

其中P_Ci为无人机在第i航迹的撞地概率；P_Di是无人机在第i段航迹被敌方雷达探测到的概率，P_Ki为无人机在第i段航迹被敌方雷达探测到并被击毁的概率^[7]。由于这些概率和地区的地形、威胁的分布密度、发现威胁的能力等都存在着很大关系，同时这些概率和无人机的各项状态（飞行高度、速度、油量等）之间的关系很难定义，即使找出他们之间关系，该公式也将十分复杂，势必将增加代价函数的计算难度。由此需要对上述的代价函数进行优化。无人机在低空突防时飞行的高度越低，被敌人发现的几率就越小，规划出的航迹飞行时间越短，越能达到出其不意的效果，同时也提高了无人机的生存概率；若飞行时间过长，会增加累计威胁，同时也增加油量的消耗。基于上述原因再结合启发式A*算法的表达式，把g(n)和h(n)分别简化为如下形式：

    起始节点到当前节点的代价函数值：

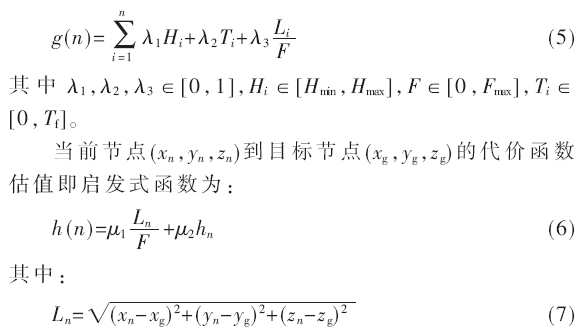
    上述代价函数表达式中L_i表示从起始点到当前节点飞行过的路程，F_max表示无人机油箱中的总的油量，H_min、H_max分别表示无人机为防止撞地的最小飞行高度和为防止被敌人雷达探测到的最高飞行高度，T_f表示无人机能接受威胁的最大门限值。启发函数中L_n表示当前节点到目标节点的距离，h_n表示目标节点的高程值，λ₁、λ₂、λ₃、μ₁、μ₂为表达式中各项的加权系数。设定不同的加权系数，获得的航迹也有所不同：如果增大高度值的系数λ₁，则规划出来的平均航迹高度就会越低，增大威胁值的系数值λ₂，则规划出来的航迹将远离威胁，同理增大航迹长度系数值λ₃，这样规划出来的航迹长度将减少。通过对这些权重系数的不同组合，可以得到所期望的满足条件的最优航迹。

1.3 算法实现

    通过结合无人机的自身限制以及任务要求，在三维航迹搜索过程中将大大缩小搜索空间，从而规划出满足条件的航迹。A*算法的实现主要是维护两个表：open表以及closed表。在三维空间中算法实现的具体实现步骤如下：

    (1)把地理威胁等环境信息初始化到规划空间中。

    (2)把起始点添加到open表中，同时把closed表置空。

    (3)判断open表是否为空，若为空则算法结束；反之，则找出open表中代价值最小的节点作为当前节点，同时把该节点从open表中删除，放入closed表中。

    (4)判断当前节点是否为目标节点，若当前节点到目标节点的距离小于最小飞行距离，则将目标节点的父亲节点当作当前节点，航迹搜索过程结束。

    (5)对当前节点进行扩展：

    ①根据约束条件产生当前节点待扩展区；

    ②对待扩展区中的每个节点，根据式(5)、(6)计算每个节点的航迹代价；

    ③如果待扩展区域中的某个节点已经在closed表中且其代价估值小于closed表中的估价值，则更新closed表中的估价值，同时把该节点移出closed表，放入open表中；如若不在closed表中，则判断该节点是否在open表中，如果不在则把该节点插入到open表中；

    ④如果该节点在open表中且open表中的g(n)值都大于当前计算的g(n)值，则更新open表中节点g(n)的值，更新后需保证open表仍然有序。

    (6)接着继续跳转到步骤(3)执行上述操作直至找到目标节点。

    由于在节点扩展时，每个被扩展的节点都会记录其父节点，当算法找到目标节点后则算法结束。接着通过从目标节点向前回溯直到起始位置，这样就得到了从起始点到目标点的最小代价航迹。

2 仿真结果    

    对上述改进后的算法在Intel Core i5、3.1 GHz的PC上进行验证试验，运行环境是Windows7操作系统。规划的空域大小为60 km×60 km，假设起始节点的坐标为(0，0，0)，目标节点的坐标为(60，60，0)，最低离地间隙为100 m，最大转弯角为45°，最大爬升/下滑角为30°。实验通过用基本A*算法和改进后的A*算法分别设置二组不同的λ₁、λ₂、λ₃、u₁，u₂值来规划最优航迹并对算法改进前后的性能进行比较分析。仿真图5的λ₁、λ₂、λ₃、μ₁、μ₂分别为λ₁=0.1，λ₂=0.3，λ₃=0.6，μ₁=0.45，μ₂=0.55，由于λ₃所占权重较大，所以规划出来的航迹总的路程较小。仿真图6的λ₁，λ₂，λ₃，μ₁，μ₂分别为λ₁=0.4，λ₂=0.5，λ₃=0.1，μ₁=0.45，μ₂=0.55，由于λ₁、λ₂所占权重较大，所以规划出的航迹飞行高度较低，安全性较高。

    两种参数的飞行高度分别如图7、图8所示。通过对比可知，第一组数据的平均飞行高度要高于第二组，这就印证了参数λ₁的大小影响无人机的平均飞行高度，飞行高度越低也间接提高了无人机的安全性，飞行高度越低，越难被敌人雷达发现。

    基本A*算法与改进后的A*算法性能比较如表1所示。通过各项数据对比可以看出，改进后的算法规划时间较改进前的少很多，并且总的航迹路程也缩减了不少，这样能够在最快的时间内规划出满足需求的最优航迹。通过改变参数λ₁、λ₂、λ₃的权重比例可以规划出更侧重于飞行高度、安全性以及飞行距离的航迹。

3 结束语

    本文通过把无人机的各项机动性能限制、飞行路程以及飞行高度等约束条件相结合的方式来缩小节点扩展时的搜索空间，同时对节点水平方向和纵向方向的空间划分，使规划出的航迹节点包含了无人机在该节点的各项状态。在三维空间中，经过限制后满足要求的节点已很少，大大提高了搜索效率，对open表结构的改进减少了open表中节点排序的时间。同时对评价代价函数进行优化，使算法能够更快地收敛到最优解。

参考文献

[1] 董文洪，易波，栗飞.无人机航路规划环境模型研究[J].计算机工程与应用，2012，48(15)：236-239.

[2] 高晖，陈欣，夏云程.无人机航路规划研究[J].南京航空航天大学学报，2001，33(2)：135-138.

[3] 宋建梅，李侃.基于A*算法的远程导弹三维航迹规划算法[J].北京理工大学学报，2007，27(7)：613-617.

[4] 赵锋，杨伟，杨朝旭，等.无人机三维航路动态规划及导引控制研究[J].计算机工程与应用，2014，50(2)：58-64.

[5] 李季，孙秀霞.基于改进A-Star算法的无人机航迹规划算法研究[J].兵工学报，2008，29(7)：789-792.

[6] 杜萍，杨春.行器航迹规划算法综述[J].飞行力学，2005，23(2)：10-14.

[7] 辛贵州.无人飞行器航迹规划算法研究[D].哈尔滨：哈尔滨工程大学，2010.