文献标识码: A
文章编号: 0258-7998(2015)04-0069-04
0 引言
在图像处理领域中,变焦技术发挥着非常重要的作用,此技术已被广泛应用于公共生活、社会安全、医疗设备以及生活的各个领域。目前有很多科研工作者开展了这方面的工作:Seung Hwan Lee等设计了一种基于色度、色差、强度模型的电子变焦算法,这种颜色模型可以改善输出图像的色彩,提高图像的清晰度和图像质量[1]。Lukac等提出了在Bayer模式上进行电子变焦,采用了一种彩色滤波阵列,可以去除图像的马赛克和块效应[2]。本文针对相机、手机等移动设备的特点,在研究了光学变焦和传统电子变焦缺陷的基础上,提出一种基于FPGA的高分辨率传感器无损电子变焦的系统设计方案,在不降低分辨率的前提下,对图像进行缩放。该方案可以通过电子变焦的模式实现光学变焦的效果,克服了光学变焦结构复杂、价格昂贵的不足,具有很大的现实意义。
缩放算法是本文基于FPGA的电子变焦系统设计的核心,目前应用于图像缩放的传统算法有:最近邻域法、双线性插值、双三次插值等。最近邻域法得到的图像质量较差,双三次插值实现复杂,双线性插值算法为一般缩放引擎使用的算法,但是当缩放系数较大时,该算法也会出现由频谱混叠带来的锯齿状效果。基于传统缩放算法的不足,本文提出一种基于抗混叠滤波的图像缩放算法。该算法根据缩放系数不同先进行滤波然后再做插值运算,克服了图像尺寸变化带来的混叠效应,即使针对较大缩放系数的情况下仍可以得到高质量的图像[3-5]。
1 变焦成像模型

光学变焦是相机通过移动光学镜头来放大或缩小拍摄的对象,光学变焦倍数越大,能拍摄的景物就越远。光学变焦示意图如图1所示。当感光器件在水平方向运动时,视角和焦距就会发生相应变化,较远的景物变得清晰,让人产生物体被拉近的感觉[6]。
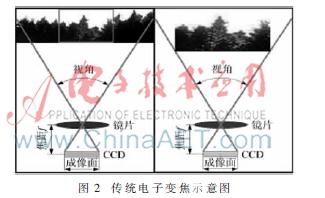
传统电子变焦是采用插值处理方式把影像照片内某一区域的像素面积扩大到整个显示窗口,从而达到放大目的,传统电子变焦示意图如图2所示。这种方法如同用图像处理软件把图片的像素放大一样,由于焦距没有发生改变,图像的清晰度会有一定程度的下降[6]。

本文提出的无损电子变焦模型采用大尺寸图像传感器采集图像,确保采集较大视场角的图像,提高变焦倍数。该模型的核心部分就是将全景图像“浓缩”到显示图像,即过采样过程。无损电子变焦示意图如图3所示,正常显示时,将全景图像缩小到显示图像输出,此时输出的图像为最大视场角图像;当放大图像时,过采样程度就会减小,将较小的图像缩小到显示图像输出;直到放大到最大时,不需要过采样,直接将原图中心显示图像大小的图像输出。这个过程不同于传统电子变焦的插值计算法,不会损失图像精度和清晰度。
2 变焦系统基本结构
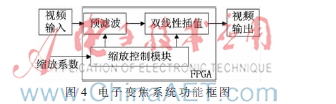
电子变焦系统功能框图如图4所示。根据设计要求,系统被划分为5个组成模块:视频图像输入模块、预滤波模块、双线性插值模块、缩放控制模块、视频图像输出模块。
FPGA作为系统的核心控制芯片,采用预滤波和双线性插值相结合的方法进行图像缩小,通过缩放系数的变化控制预滤波方式和插值位置。外部设备采集2 560×1 440分辨率的视频图像,缩放控制模块根据缩放系数控制预滤波模块选择合适的滤波模板,以及为双线性插值模块提供插值坐标和插值系数。最终视频图像经VGA输出320×240分辨率的视频图像,从而实现6倍光学变焦的效果。预滤波模块根据缩放系数选择不同的滤波器进行滤波,从而消除图像缩小带来的频谱混叠。插值模块采用双线性插值法实现图像的缩放。控制模块根据缩放系数的变化,为预滤波模块选择合适的滤波器,同时控制插值模块生成合适的插值坐标和插值系数,实现全局控制。
3 缩放算法分析
3.1 频谱混叠

式(1)中x(t)为连续信号,x(n)为抽样信号,抽样间隔为T,若将抽样频率fs减小到(1/M)fs,最简单的方法是将x(n)中每M个点抽取一个,组成一个新的序列x′(n):
x′(n)=x(Mn),n=-∞~+∞(2)
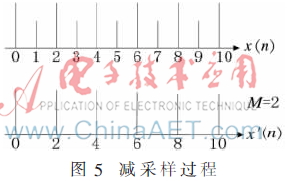
上述过程为减采样过程,图5所示为抽样频率减小2倍的结果。
下面讨论x(n)和x′(n)的频域关系,现定义一个中间序列x1(n):

式中p(n)是一脉冲串序列,它在M的整数倍处值为1,其余为0。
显然:
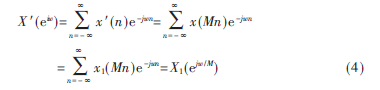
而

所以:

式中X′(ejw)和X(ejw)分别是x′(n)和x(n)的DTFT。从式(6)中可以看出,X′(ejw)是原信号频谱X(ejw)先做M倍的扩展再在w轴上每隔2/M的移位叠加。由抽样定理可知,在第一次对x(t)抽样时要保证fs≥2fc(fc为x(n)的最高频率,fs为抽样频率),则抽样结果不会发生频谱混叠[7]。当对x(n)作M倍抽取后,若保证x′(n)重建x(n),则X′(ejw)的一个周期(-/M~/M)也应等于X(ejw),这样要求抽样频率fs≥2Mfc,如果不满足将发生频谱混叠。因此理想的抗混叠滤波器为:

3.2 频谱混叠仿真

数字图像是通过对模拟图像进行等间隔采样得到的,需满足采样定理,即最高频率在采样频率的1/2附近,因此一幅数字图像中不同区域交界处的频率在频谱的附近[8]。本文采用环形图像进行仿真,如图6所示,该图像为同心圆环,并且圆环从内到外的频率在慢慢增加。通过对该图像进行频率分析,可以获得该图像的频谱特性。首先进行一维数据的频谱混叠分析,然后推广到二维图像。
对于一维频谱,抽取该图像的中间一行进行分析,图像的大小为301×301像素,抽取第150行数据进行分析,记为x(k),对其进行一维离散傅里叶变换记为X(K),时域及频域显示如图7所示,其中时域和频域都进行了归一化处理。
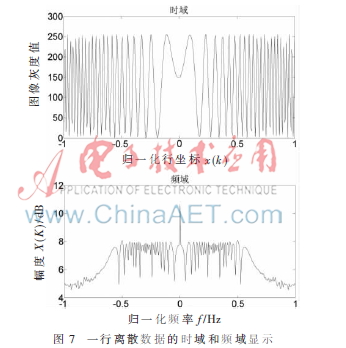
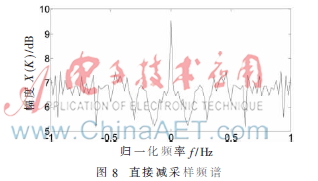
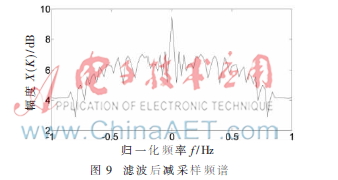
从频域可以看出,图像的信息集中在低频区域,主要在[-0.5,0.5]之间,高频区域信息较少。首先,直接对该数据进行3倍减采样,求其DTFT并观察其频谱,直接减采样频谱图如图8所示;其次,用凯赛窗设计一个FIR低通滤波器,截止频率为0.3,阶数为30,对该数据进行滤波后再求其DTFT,观察滤波后减采样频谱如图9所示。从频谱图中可以发现直接减采样的数据发生了严重的频谱混叠现象,而经过低通滤波再减采样的数据没有发生频谱混叠,只是频谱有所扩展。

同样推广到二维图像,对上述图像缩小3倍。首先,直接采用最邻近插值的方法将图像缩小3倍,直接减采样如图10所示;其次,使用窗函数法设计一个低通滤波器,阶数为21阶,截止频率0.3,对图像进行低通滤波,然后再使用最邻近插值缩小图像,滤波后减采样效果如图11所示。对比两幅图可知,直接减采样图像产生了混叠,有明显的锯齿现象,滤波后减采样图像没有发生混叠,图像平滑,但是因为使用了低通滤波器使高频信息受损,因此需要设计合适的滤波器,既要抑制混叠又要保留适当的高频信息。
3.3 滤波器设计
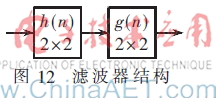
本文的缩放模块是采用先滤波、后采样的方式,对每种缩放系数采用合适的抗混叠滤波器。根据FPGA的内部结构以及输入输出图像的大小,缩放模块的缩放系数选取1~1/6(约64/64~11/64),这样可分为53级缩放。基于FPGA硬件存储资源的考虑,不可能每种缩放系数都采用不同的滤波器,因此当缩放系数在一定范围变化时采用同一种滤波器。本文设计使用两级滤波的形式,产生多种不同的滤波器,根据缩放系数的大小选择滤波系数和滤波级数。滤波器结构如图12所示。具体分为5个系数范围,在这5个系数范围分别采用合适的滤波器,使用预滤波与双线性插值相结合的方法进行图像缩放。
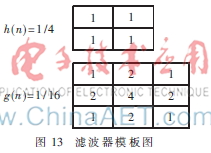
采用两个滤波器模板,实现多种组合,可以应对不同的缩放系数。本文选用图13所示的两个滤波器模板进行滤波,实现5种不同组合,分别对应5种缩放范围。
通过理论分析和仿真研究得到以下结论(代表卷积):

4 图像评价
本文研究的是图像缩小,首先将原图缩小到目标图像,其次在PC机上使用Lanczos插值算法缩放到相同尺寸,以该图像作为参照图像,进行客观的比较。Lanczos插值算法是比较好的图像处理算法,既可以抑制图像混叠又可以保护图像的边缘,在混叠和锐化之间进行了权衡,通过实验发现采用该算法进行图像缩放可以得到较好的效果[9]。本文选取6幅有代表性的图像,如:风景、人物、房屋等进行综合评价,比较图像质量。对选取的图像分别采用最邻近插值、双线性插值和三次立方插值以及抗混叠滤波缩放算法进行缩放,从主观和客观角度上进行评价。
4.1 主观评价
图14是将原图缩小3倍的部分图像,可以发现最邻近插值得到的图像锯齿现象加重,图像变得更加锐利,双线性插值算法也会出现轻微的锯齿现象,图像较模糊;抗混叠滤波缩放算法得到的图像在直观上要优于前两种算法,图像较清晰。
4.2 客观评价
分别对上述6幅图像进行缩放,比较在各种算法下的峰值信噪比,结果如表1、表2所示。
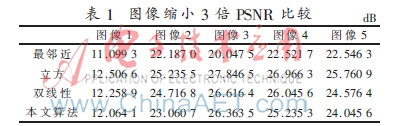
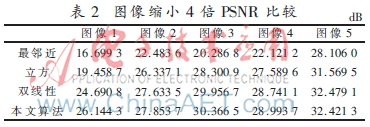
当缩放系数不是很大时,由于缩放前进行了预滤波,在客观比较上峰值信噪比可能不如双线性和立方插值,但是由于算法插值前进行了预滤波,这样有效抑制了频谱混叠的发生,从直观上看优于最邻近插值和双线性插值,随着缩放系数的增大抗混叠滤波缩放算法得到的峰值信噪比提高,明显优于双线性和立方插值算法。
5 小结
本文提出了一种基于高分辨率传感器的无损电子变焦模型,该技术区别于传统的电子变焦模型,变焦过程不损失图像精度和清晰度,进而实现通过电子变焦达到光学变焦的效果。缩放算法使用一种抗混叠滤波器和双线性插值相结合的图像缩放算法,该算法有效避免了图像缩小带来的混叠现象。从仿真中可以发现,当缩放系数较小时,由于双线性插值存在低通滤波的效果,因此不需要再进行滤波,双线性插值适应的缩放范围为1~1/2。当缩放进一步扩大时,双线性滤波已经不能满足要求,这样需要在插值前进行预滤波,本文使用两级滤波结构产生多种滤波器,根据不同的缩放系数使用不同的滤波器。通过仿真比较,当缩放两倍以上时,该算法优于双线性和立方插值,同时硬件实现简单。
参考文献
[1] Seung Hwan Lee,Dong Hwan Koh,Yang Wang,et al.DigitalZoom based on HCI ColorModel(Hue-Chroma-Intensity)[C].Intelligent Systems Modelling & Simulation (ISMS),2013 4thInternational Conference on,29-31 Jan.2013.
[2] LUKAC R,MARTIN K,PLATANOITIS K N.Digital camera zooming based on unified CFA image processing steps[J].Consumer Electronics,IEEE Transactions on,2004,50(1):15-24.
[3] 谭亮,孙俊喜,顾播宇,等.基于FPGA局部视频图像任意比例缩放系统[J].电视技术,2013(9):42-44.
[4] 严利民,田锋,顾裕灿.图像缩放算法的研究及FPGA实现[J].仪表技术,2012(7).
[5] Alakarhu Juha,Salmelin Eero.Partinen Nokia PureView oversampling technology proceedings of SPIE-The International Society for Optical Engineering,v8667,2013.
[6] 王金华,严卫生,刘旭琳,等.基于视景通道的透镜成像过程仿真技术研究[J].系统仿真学报ISTIC PKU,2010(9).
[7] 贾中云.一种利用采样率转换方法的灰度图像放大算法[J].杭州师范学院学报:自然科学版,2005(5):360-363.
[8] 李秀英,杨杰,王丽平.用于改变图像大小的M带插值滤波器设计[J].现代电子技术,2005(9):28-29.
[9] 张善文,戎蒙恬,李萍.基于非均匀采样重构的图像插值算法[J].信息技术,2011(3):1-4.

