0 引言

　　交通系统是城市经济活动的命脉，也是衡量一个城市文明程度的重要标志，同时对城市的经济发展和居民生活水平的提高起着极为重要的作用。城市道路交通的拥挤严重影响着居民生活，并造成社会生产力的极大浪费。如何有效地缓解交通拥挤，提高交通系统效率，成为世界各国亟待解决的问题。在城市交通网中交通干线承担了城市交通的主要负荷，因此，在不增加道路的前提下，对干线交通灯的智能协调控制成为缓解交通压力的主要手段，也是目前各国学者研究的重点。如Little等建立了最大绿波带宽的MAXBAND模型，提出了干线双向绿波协调控制配时策略[1-2]；卢凯等利用分析时距的方法，给出了进口道单独放行条件下的干线双向绿波协调控制数解算法[3]；徐世洪等人基于交通流的动态模型，提出了一种双向绿波的干线相邻路口相位差优化控制方法，并应用自适应遗传算法进行改进求解，实现了交通干线分级递阶协调控制[4]。本文依据干线协调控制原理，提出一种基于粒子群算法交通干线控制策略。以车辆行驶过程中延误时间最小为优化目标[5]，建立交通干线双向绿波控制延误模型，并通过该控制策略进行优化控制。最终通过实验结果对比验证了该控制策略的有效性。

1 干线总延误模型的建立

　　城市干线交通信号的控制参数有：各交叉口的信号周期、绿信比以及相位差。干线交通信号的协调控制就是将干线上若干相邻交叉路口的信号进行协调配时，使进入交通干线的车队不遇或少遇红灯，以达到减少延误的目的。

　　1.1 相位的确定

　　相位是指在周期时间内按需求人为设定的某个方向上的交通流(或几个方向上的交通流的组合)，同时得到通行权的时间带。

　　干线系统的特点是干线方向车流量远远大于非干线方向车流量，且车流量以直行车流为主。但在实际中，即使左转的车流量不大，如果不加以单独控制，也会对直行车流产生较大干扰。因此，相位划分如图1所示。

　　1.2 模型的基本假设

　　由于交通系统的随机性、模糊性和不确定性，延误模型的建立基于以下基本假设：

　　(1)相位转换中的黄灯时间通常为2 s，将其归入相位转换的红灯和绿灯时长内，相位转换无时滞；

　　(2)保持每个信号周期的相位数和相位放行顺序固定不变；

　　(3)干线控制系统内部的交通流为非饱和流；

　　(4)车辆到达交叉口看作是点到达；

　　(5)系统内非协调相位方向上的车流采用随机到达方式处理，根据Webster延误模型计算[6]；

　　(6)系统内干线方向上由于交叉口相互间距不宜过大，交通流受上游交叉口信号影响而不再随机。

　　1.3 模型的建立

　　在干线协调控制系统中，设主干线方向上的相位为协调相位，其余方向上的相位设为非协调相位，故车辆延误分为协调相位的延误和非协调相位的延误两部分。

　　若车队驶向交叉口未受阻，即在绿灯期间可以完全通过，则时间延误为0。若行驶车队受阻，则受阻情况分为：车队在到达交叉口时第一辆车就遇到红灯，导致整个车队全部受阻；在信号变为红灯时车队已部分通过交叉口，导致车队局部受阻。

　　(1)协调相位车队全部受阻延误模型

　　干线系统中车辆行驶方向分为上行方向和下行方向，上行车队从交叉口i到i+1途经路长为li，i+1，上行方向的平均车速为vup，车队第一辆车遇到红灯的等待时间为tw，up，交叉口i到i+1的相位差是?椎i+1，i。则分析可得：

　　车队通过交叉口i+1的通行能力为ui+1，红灯时长为tred，绿灯时长为tgreen，交叉口疏散累积车辆需tgo，up，在变为绿灯之后到达的车辆不受阻地通过交叉口i+1，则：

　　qi+1，up(tw，up+tgo，up)=tgo，up·ui+1(2)

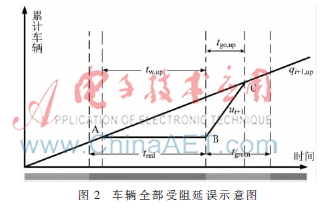
　　如图2所示，△ABC的面积即为协调相位中上行方向车队全部受阻的延误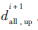。即：

　　在式(3)中，当时车辆全部受阻。相邻两交叉口i与i+1之间的相位差之和为周期C，即i+1，i+i，i+1=C。同理可知，下行方向的车流量全部受阻时协调相位延误为：

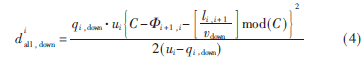
　　(2)协调相位车队局部受阻延误模型

　　当mod(C)<i+1，i时，在车队行驶至交叉口i+1时，一部分车辆无阻碍通过，而余下车辆受阻。受阻车辆等待时间为红灯时长tred，绿信比为?姿。在受阻过程中，未赶上绿灯的受阻车辆有qi+1，up·tred辆，当下一周期绿灯信号到来时需要经过t，受阻车辆全部通过交叉口。由此可得：

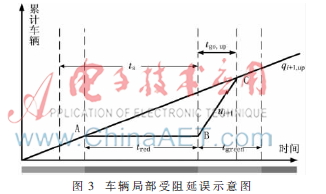
　　如图3所示，S△ABC即为协调相位方向上车队上行方向局部受阻的延误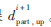。即：

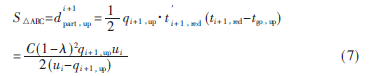
　　同理可知，下行方向车流量局部受阻时协调相位的延误为：

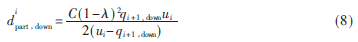
　　综上所述，引入变量 ?琢i设定两种情况，上行车队在交叉口处协调相位的延误表达为：

　　在式(9)中，如果车辆全部受阻，则取 i=1；如果车辆局部受阻，则取 i=0。

　　同理，引入变量?茁i设定下行车队两种情况在交叉口处协调相位的延误为：

　　在式(10)中，如果车辆全部受阻，则取?茁i=1；如果车辆局部受阻，则取i=0。

　　(3)非协调相位车队延误

　　在干线系统中，饱和率小于1，并且非协调相位车流随机到达，所以可以根据 Webster 延误模型计算每一辆车的平均延误：

　　式中，qi是相位i平均车辆到达率，单位为辆/时(pcu/h)； i为相位i的饱和度。

　　式(11)中第一部分是均匀车辆所产生的延误，第二部分是随机车辆所产生的延误，将两部分求和减去校正部分(通常情况下，校正部分可以忽略)，因此，系统中的非协调相位的延误模型为：

　　式中， qik表示第i个交叉口第k相位的车流量，dik表示第i个交叉口第k相位的车辆平均延误。

　　综上所述，干线系统的总延误为：

　　在式(13)中，引入加权因子?滓，当?滓=1时，只考虑协调相位的延误；只考虑非协调相位的延误；当(0，1)时，则为同时考虑协调相位和非协调相位的总延误。

2 改进的粒子群算法干线协调优化

　　城市交通信号控制系统是一个典型的多输入多输出的复杂系统，必须尽可能将干线协调控制参数同时优化。而且，相比其他优化方法而言，粒子群算法的速度快，效率高，更适用于干线交通延误模型优化求解。

　　2.1 基本的粒子群算法

　　1995年，Eberhart 博士和Kennedy 博士受到飞鸟集群活动的规律性的启发，针对鸟群捕食行为的研究提出粒子群算法(PSO)[7]。

　　PSO优化算法的速度公式(14)和位置公式(15)持续更新如下所示：

　　式中，为粒子的速度；w为惯性权重，通常取值在0.1~0.9之间；为当前粒子的位置；r是介于(0，1)之间的随机数；c1，c2为加速常数。

　　2.2 改进的粒子群算法

　　传统PSO算法收敛速度较其他进化算法快，但容易陷入局部极小点。因此，文献[8]提出一种新的粒子群优化算法——历史最优共享的粒子群优化算法(VSHBPSO)。VSHBPSO的核心思想：原粒子与一切具有优良基因的粒子交互，不断趋向优良，同时粒子的更新还向之前实验中搜索的全局历史最优位置学习。

　　基于历史最优共享PSO算法更新位置公式为：

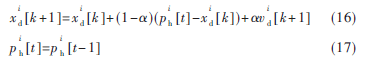
　　改进的PSO算法采用十局运行机制：每一次实验结束所得全局最优解应用在下一次运算过程中，以此类推，取最终得到的最优解。

　　2.3 算法实现步骤

　　根据以上分析，改进的历史最优共享的粒子群算法的实现步骤为：

　　(1)设置算法的参数和最大迭代次数，初始化种群X(k)使每个粒子m产生初始速度组成V(k)。

　　(2)计算种群在搜索空间中每一维的适应值。

　　(3)将粒子当前适应值与自身的历史最优值和种群历史最优值分别进行比较，如果p的值不如当前值，则置当前值为空间内自身的历史最优解；如果p的值不如当前值，则置当前值为空间内种群的历史最优解。

　　(4)按照速度更新式(14)和位置更新式(16)、(17)对粒子的速度和位置进行更新，并形成新的种群X(k+1)。

　　(5)查看是否符合算法结束条件，如果符合则算法结束，求得最优解；否则，迭代数加1，即t=t+1，并跳转至步骤(2)。

3 仿真实验研究

　　为验证所建立的模型的有效性，利用秦皇岛市河北大街中段车流量较大的3个交叉口(友谊路路口、红旗路路口和海阳路路口)作为仿真实验对象。

　　3.1 实验路段数据统计

　　统计实验路段各交叉口一天内的车流量并绘制曲线图，如图4所示为友谊路口的车流饱和度。

　　在图4中可以看出，一天中的车流量饱和度均呈现为小于0.9的非饱和状态，理论上适用于双向绿波协调控制。而早晨上班时段和下午下班时段属于高峰期，白天时段车流量属于平峰期，晚上23点以后至次日清晨车流量较低。

　　实验路段的路况信息如表1所示。

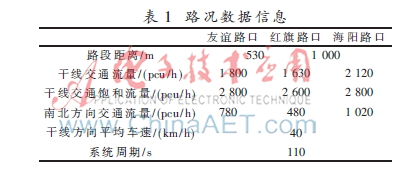
　　3.2 参数设定

　　优化目标函数可以描述为使式(18)中总延误D获得最小值的最优控制方案：

　　选取3个交叉口中最大的周期作为系统周期。定义粒子种群，设定种群规模为n=50的5维粒子群，学习因子c1=c2=2，惯性权重w为0.9~0.4线性下降，最大迭代次数为100。

　　3.3 结果分析

　　以路段的平峰时期流量为例进行分析。

　　(1)当协调相位车流量远远大于非协调相位时，即只考虑协调相位的主干线双向绿波控制，实验结果如表2所示。

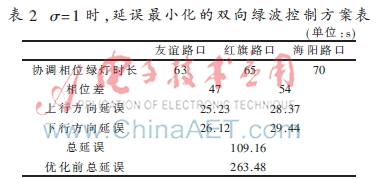
　　由实验结果可知，在相同路段条件下，采用延误最小控制方案可以大大减小延误时间，有效提升通行效率。

　　(2)当协调相位和非协调相位交通流量均考虑时，协调相位延误的权值占总延误权值的 3/4，支路延误权值占总延误权值的 1/4，实验结果如表3所示，时距图如图5所示。

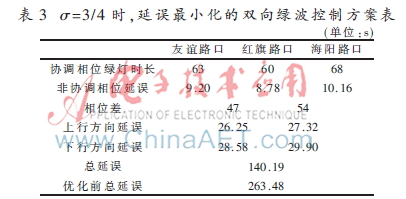
　　非协调相位上的车流在绿灯时间内可以通过交叉口，因此考虑非协调相位延误通行效果明显优于传统定时控制方案。

　　用此方案进行10个周期的仿真实验，并与传统定时控制方案中的延误对比，如图6所示。

　　由此可见，优化后的最小延误控制方案能够减小约41.3%的时间延误，有效地提高了城市交通干线的通行效率。

4 结论

　　本文在常态交通情况下建立了干线总延误模型，并以总延误最小为优化目标，协调绿信比和相位差来实现交通干线双向绿波控制。在所建立的模型中考虑非协调相位对主干线车流的影响，并引入加权系数更合理地展现实际路况；实验部分对城市交通干线进行实地调查，获得更符合实际交通情况的干线数据；通过将实际数据代入模型进行仿真实验，验证了此种控制策略的有效性，对改善城市交通拥堵情况具有积极的现实意义。

　　参考文献

　　[1] LITTLE J D C.The synchronization of traffic signals by mixed-integer linear programming[J].Operations Research，1966，14(4)：568-594.

　　[2] LITTLE J D C，KELSON M D，GARTNER N H.MAXBAND：a versatile program for setting signals on arteries and trian-gular networks[R].Cambridge: Massachusetts Institute of Technology，1981，12(3)：134-141.

　　[3] 卢凯，徐建闽，李轶舜．进口单独放行方式下的干道双向绿波协调控制数解算法[J]．中国公路学报，2010，23(3)：95-101．

　　[4] 徐世洪，李志敏，戴高，等.基于自适应遗传算法的相位差优化模型研究[J].交通信息与安全，2011，29(2)：13-18.

　　[5] 沈国江，许卫明.交通干线动态双向绿波带控制技术研究[J].浙江大学学报，2008，42(9)：1625-1630.

　　[6] 赵雨旸，冯雨芹，杨忠良.信号交叉口Webster法延误计算修正模型[J].黑龙江工程学院学报：自然科学版，2010，24(2)：8-11.

　　[7] EBERHART R，KENNEDY J.A new optimizer using parti-cle swarm theory[C].IEEE Proceedings of the 6th Interna-tional Sympo-sium on Micro Machine and Human Science.Piscataway：IEEE Service Center，1995：39-43.

　　[8] 林蔚天.改进的粒子群优化算法研究[D].上海：华东理工大学，2012.