0 引言

　　MEMS陀螺接口电路的数字集成化已经成为MEMS陀螺发展的一个最热门的方向，所以高性能模数和数模转换器对于数字陀螺接口电路的集成就变得格外重要[1]。如图1所示，在一个数字陀螺的经典系统结构中，DAC担负着将DSP处理后的数字信号转换为模拟信号的作用，然后将模拟信号反馈给陀螺，从而实现闭环数字控制的功能，用来保证整个系统的稳定。相对于传统的耐奎斯特数模转换器而言，Sigma-Delta数模转换器能够实现更高的精度，这对于提升MEMS数字陀螺系统的整体性能而言具有非常重要的现实意义[2]。此外，针对于多位量化数字调制器的内部DAC不匹配导致的非线性问题，对DWA模块进行了改良设计，并且通过FPGA验证，得到了预期的结果。

1 Σ-ΔDAC结构

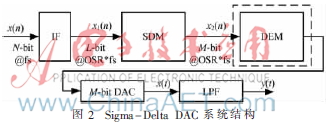
　　一个典型的Σ-Δ DAC的系统结构如图2所示。输入数字信号x(n)是经过耐奎斯特频率fs采样得到的。数字插值滤波器的主要功能是对数字信号进行二次采样，从而提高数字信号的采样频率，x1(n)的位数L大于或等于x(n)的位数N。信号x1(n)通过Sigma-Delta数字调制器进行量化来降低输出精度，并抑制量化噪声。当输出的位数M>1时，内部M位DAC由于器件之间存在失配误差，会产生非线性问题[3]。因此需要采用动态单元匹配技术(DEM)减小内部M位DAC的非线性[5-7]。

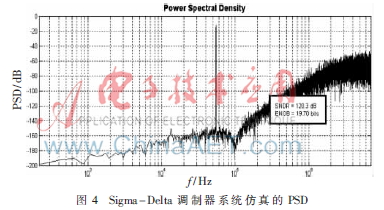
　　综合分析各个结构的优缺点，折中考虑后，本文中的Σ-Δ数字调制器最终采用了三阶四比特量化的单环前馈结构(CIFF)。图3为NTF经过零点优化后的最终结构，经过零点优化的结构其量化噪声能够显著降低，并且稳定性也得到显著提高。图4为系统结构的仿真结果。当输入信号为频率为50 kHz、归一化信号幅度为0.5的正弦波，系统的采样频率为12.8 MHz时，得到输出功率谱密度（PSD）。在100 kHz的信号带宽内，系统的SNDR能够达到120.3 dB，有效位数达到19.7位，满足数字陀螺的性能要求。

2 改进型DWA

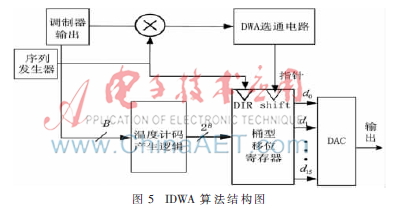
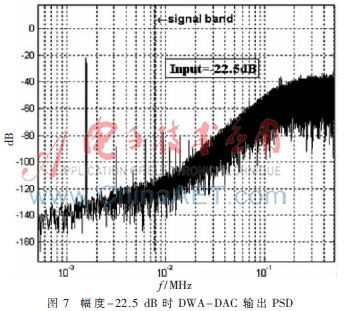
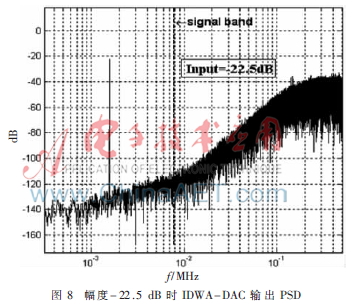
　　动态元单元匹配技术（DEM）是一种对D/A转换器中温度计码线性化处理的方法，而数据加权平均（DWA）由于具有整形效果明显、硬件实现简单、节省硬件开销等特点而最为常见。向调制器输入小幅度的信号时，数字调制器的输出代码值将大部分集中在中间值及其附近，这相当于连续向内部DAC输入固定直流值。因此，动态匹配单元的误差将会周期化，即在基带内产生噪声。本文使用的改进的DWA(IDWA)的基本思想是通过增加单元DAC的数量[8]，使得单元DAC的数量大于调制器的量化等级，以此来解决上述问题。图5是IDWA的算法结构图。图6 是IDWA中的单元选择逻辑(ESL)模块框图。IDWA与传统DWA模块相比还具有一些优点。首先IDWA系统反馈回路中的输入以及求和端均可以使用B位有符号信号，而不必为DWA中的B+1和B+2位有符号信号；其次是在DWA系统反馈回路的反馈信号中，不必使用求余算法，降低了系统结构的复杂性。在Matlab中建立DWA-DAC和IDWA-DAC系统，进行仿真对比。当向两种系统输入幅度为-2.5 dB、频率为20 kHz的信号时，都能完成失配误差整形，产生的杂波被整形到高频处。但如果幅度降低到-22.5 dB时，情况会变得不同。图7和图8分别是输入幅度-22.5 dB时的DWA-DAC输出功率谱和IDWA-DAC输出功率谱。由图中可以看出DWA-DAC输出功率谱信号带宽内出现了寄生杂波，产生的失真将会降低调制器的动态范围，而相同条件下的IDWA-DAC仍然能够很好地完成失配误差整形，保证了带宽内的信号精度。因此通过对比可以发现，当向数字调制器输入小幅度信号时，相比于典型的DWA算法，IDWA算法能够有效提高调制器的动态范围。

3 仿真结果

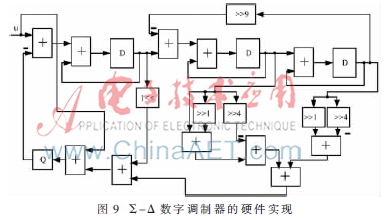
　　本文中Sigma-Delta数字调制器的硬件实现如图9所示，其中的各个参数都采用了CSD编码优化，可以大幅度地减少硬件的消耗。

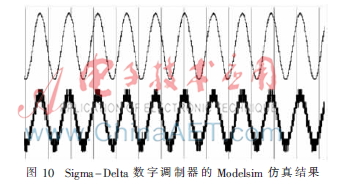
　　对调制器进行Verilog代码实现，整个系统在modelsim下的仿真结果如图10所示。从波形上可以看到，此结构实现了多位量化Σ-Δ数字调制器的功能。

4 FPGA验证结果

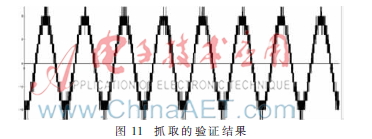
　　最后利用FPGA进行Σ-Δ数字调制器的综合和验证,本文使用的FPGA芯片是Xilinx公司Spartan3E系列XC3S500E产品。经过综合后输入频率50 kHz的正弦波，采样率为12.8 MHz，经过FPGA处理之后，图11为利用Chip Scope Pro抓取的波形。将Σ-Δ数字调制器输出数据从FPGA中导出，对导出的数据进行FFT运算，二次谐波小于-140 dB，三次谐波小于-135 dB，最大信噪失真比能达到120 dB，有效位数能达到19位以上，满足设计要求。

　5 结束语

　　本文设计了一款三阶四位量化的Σ-Δ数字调制器，并且对DWA结构进行了算法改进。最后利用FPGA验证了设计的正确性，达到了设计要求，实现了预期的设计目标。

　　参考文献

　　[1] LIN L，LIU D，CUI J，et al.Digital closed-loop controller design of a micromachined gyroscope based on auto frequency swept[C].IEEE International Conference on NEMS，2011(6)：654-657.

　　[2] GE F，LIU D，LIN L，et al.Fast self-resonant startup pro-cedure for digital MEMS gyroscope system[C].The 7th IEEEInternational Conference on NEMS，March 2012：669-672.

　　[3] RODJEGARD H.A digitally controlled MEMS gyroscope with 3.2 deg/hr Stability[C].Digest of Technical Papers.IEEE Transducers’05，The 13th International Conference on Solid-State Sensors，Actuators and Microsystems，June 2005(1)：535-538.

　　[4] Li Bingxin.Design of multi-bit sigma-delta modulators for digital wireless communications[D].PhD dissertation，Royal Institute of Technology，2003：40-45.

　　[5] WELZ J，GALTON I.Necessary and suffcient conditions for mismatch shaping in a general class of multibit DACs[J].IEEE Trans.CircuitsSyst.II，Analog Digit.Signal Process.，2002，49(12)：748-759.

　　[6] Sun Nan.High-order mismatch-shaped segmented multibit Σ-Δ DACs with arbitrary unit weights[J].IEEE Transac- tions on Circuits and Systems I，Feb.2012，59(2)：295-304.

　　[7] GALTON I.Why dynamic-element-matching DACs work[J].IEEE Transactions on Circuits and Systems II，2010，57(2)：69-74.

　　[8] VADIPOUR M.Techniques for preventing tonal behavior of data weighted averaging algorithm in sigma delta modulator[J].IEEE，Circuits and Systems II，2000，47(11)：1137-1144.