0 引言

    信任函数理论是以信任函数为信任量化模型的数学理论的统称，是一种高效的不确定性信息表达和融合工具^[1]。然而在证据高度冲突时，利用经典Dempster组合规则会产生有悖于常理的结果，为此学者们对证据冲突进行了分析^[2-4]，提出了许多改进算法^[5-11]。另一方面，Dempster组合规则还存在焦元基模糊问题，即将基数较大焦元（携带确定性信息不多）上的基本信任过多地聚焦到基数较小焦元（携带更多的确定性信息）上。

    本文首先简要介绍信任函数理论，并梳理现有改进的融合目标识别算法，然后提出一种修正算法。修正算法采用局部冲突信任质量局部重分配的策略，同时考虑了焦元基数对一致信任质量组合的影响。最后进行算例与仿真比较分析，结果验证了该方法的合理有效性及优越性。

1 信任函数理论基础

    信任函数理论通常建立在有限个互斥元素组成的完备集合Θ上。Θ称为辨识框架，包含对拟解决问题的所有已知结果。

    Dempster组合规则反映证据的联合作用，满足交换律与结合律，其中1/(1-κ)称为归一化因子，它是该理论中的融合目标识别规则。然而在证据间高度冲突时，利用Dempster组合规则会产生有悖于常理的结果，如著名模糊数学专家Zadeh提出的反例。此外该规则在证据间冲突较大时对冲突的变化过于敏感^[12]。

2 现有改进算法

    Dempster规则将冲突信质按组合后的BBM成比例地分配给组合后各焦元，造成组合过程偏向各证据间的相容部分。Yager^[5]认为，在没有更多信息的条件下，应该将冲突的信质赋予未知领域Θ。Dubois与Prade^[6]则认为，应将冲突信质赋予相互冲突焦元的并集，使得局部冲突局部分配，该策略比Yager组合规则更精确。Smets^[7]认为冲突是由于辨识框架θ不完备导致的，因此建议将冲突信质赋予空集φ，表示真实结果存在于辨识框架外。Dezert&Smarandache^[8]则认为，辨识框架中各元素并非完全互斥，于是考虑了辨识框架中元素的交集命题。国内学者邓勇^[9]对Yager方法提出一种改进，认为冲突信息也有部分可以利用，并非将所有冲突信质赋予未知项。郭华伟^[10]提出一种新组合规则，采用局部冲突局部分配策略，但同样需对所有证据进行总体分析才能得到分配系数。以上各种改进方法主要解决Dempster组合规则的归一化问题，也即冲突再分配问题。对此Lefevre^[12]提出一种统一规则，以上改进算法都是Lefevre规则的特例。

    对组合中赋予非冲突焦元(即两证据焦元的交集为非空)的BBM，Dempster组合规则同样存在问题。Voorbaark^[13]就曾指出Dempster组合规则偏向基数较大的焦元。王壮^[11]对此提出PBAR组合规则（即基于均衡信度分配准则的组合规则)。但PBAR组合规则在处理焦元基模糊问题时，一个焦元命题的基数增大会使得另一命题获得更多的BBM，在处理冲突问题时，只要是冲突命题都用证据距离加权，未对组合中产生冲突的两个命题进行个体分析。

3 修正的融合目标识别算法

    针对上述问题及现有改进算法存在的不足，本文提出一种修正融合目标识别算法。

    在没有更多信息条件下，一个复合命题的BBM应均等地分配于单元素子命题，因此在参与合成的两个命题中，分配给两命题交集的BBM正比于g(Ai I B_j)；而剩余BBM按比例留在原命题中，归一化处理后如式(2)所示。该方法可克服Dempster组合规则将基数较大焦元(携带确定性信息不多)的BBM过多地聚焦于基数较小焦元(其携带的确定性信息相对较多)；当两个原命题等价时，加权系数g(A_i I B_j)/[m₁(A_i)+m₂(B_j)]为1，而当交集基数相对两个原命题的基数很小时，系数g(A_i I B_j)/[m₁(A_i)+m₂(B_j)]趋于0，大部分BBM成比例地留在原命题中。假设赋予A_i与B_j的BBM不变且|A_i|与|A_i I B_j|不变，当|B_j|逐渐增大时，不影响留在原命题A_i中的BBM，而留在B_j中的BBM逐渐增多，赋予两命题交集的BBM逐渐减少，反之同样成立。这符合直观理解。

    当A_i I B_j=φ时，m₁与m₂分别给两个冲突的命题赋予了基本信任质量，也即m₁与m₂对应的证据发生了冲突。局部看，两批证据对两个冲突命题赋予的BBM值有大小差别。若两个BBM值大小相等，则难以区分两个冲突命题。为叙述方便，定义一个倾向性因子。

    基于以上分析，当A_i I B_j=φ时，采用如式(3)所示组合规则形式。当β_ij恒为0时，即Lefevre的Proposition1(简称Lefevre-1)方法^[12]；当β_ij恒为0.5时，即Lefevre的Propositon2方法^[12]；当β_ij恒为1时，即Dubois&Prade(简称DP)方法[6]。

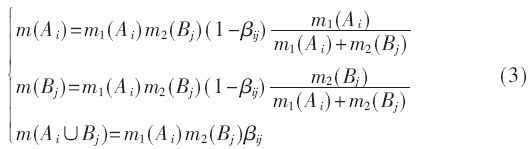
    新规则克服了Lefevre^[12]所提规则参数过多，在实际中难以确定的问题，只要确定在冲突情况发生时分配给两个命题并集的比例系数β_ij，剩余BBM值按比例分配给原命题，无须额外信息。

4 算例与仿真比较分析

    (1)算例1。为比较分析各组合规则对冲突大小的敏感性，构造该算例。假设辨识框架为Θ={θ₁，θ₂，θ₃}，2个BBA分别为：m₁({θ₁})=0.9-δ，m₁({θ₂})=0.1，m1({θ₃})=δ；m2({θ₁})=δ，m2({θ₂})=0.1，m₂({θ₃})=0.9-δ，其中δ∈[0.0001，0.25]。

    不同组合算法赋予不同命题BBM随冲突系数κ的变化曲线如图1所示。在冲突剧烈情况下，κ的微小变化使Dempster组合规则对赋予命题{θ₁}的BBM出现急剧下降。本文方法赋予命题{θ₁}的BBM比Dubois&Prade规则高，但不如Lefevre-1规则。主要因为当两个命题相互冲突时，本文将部分BBM赋予两个命题的并集，而Lefevre-1规则对冲突信质进行加权平均处理。本文方法与Dubois&Prade规则赋予命题{θ₁，θ₃}的BBM一致，因为当两命题冲突时，两批证据赋予冲突命题的BBM相同，如m₁({θ₁})>0，m₂({θ₃})>0而m₁({θ₁})=m₂({θ₃})，本文方法认为此时两个命题在组合过程中难以区分，于是采取与Dubois&Prade规则相同的处理方法，将BBM赋予两个命题并集。当两批证据赋予冲突命题的BBM不同时，如m₁(A_i)>0，m₂(A_j)>0而A_i I A_j=φ，m₁(A_i)≠m₂(A_j)，本文方法与Dubois&Prade规则不同。

    (2)算例2。设某识别系统的传感器依次收到4批证据，辨识框架为Θ={θ₁，θ₂，θ₃}，其BBA如表1所示。

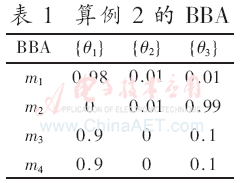
    各组合算法的结果如表2所示。由表2可看出，当前两批证据组合时，本文方法在命题{θ₁}中还留有部分BBM。本文方法与Dubois&Prade规则、PBAR规则赋予命题{θ₁，θ₃}上的BBM都较大，当仅有这两批证据时，一个支持{θ₁}，一个支持{θ₃}，在没有更多信息条件下，难以确定哪个是正确答案，因此大部分信质赋予两个命题的并集。当收到第三批证据时，邓勇规则、PBAR规则与本文算法都得出了正确结论，但邓勇规则是基于对所有证据的全局分析对全局冲突全局分配的，且组合结果的不确定性过大。PBAR规则赋予命题{θ₁}的BBM比本文方法大，但在获得第四批证据时，本文方法赋予命题{θ₁}的BBM比PBAR方法略大。Dubois&Prade规则却在获得第四批证据时，赋予命题{θ₁}的BBM与只有三批证据相比却降低了，由0.882 0变到了0.810 9。

5 结束语

    本文在比较分析部分现有改进组合规则的基础上，提出一种修正融合目标识别算法。该算法采用局部冲突信任质量局部重分配策略，同时考虑焦元基数对一致信任质量组合的影响，能较好地同时解决冲突分配和焦元基模糊问题。未来值得进一步研究的方向包括证据的不确定性、不一致性及证据间冲突大小的度量等。

参考文献

[1] LIU Z，PAN Q，DEZERT J.A new belief-based K-nearnest neighbor classification method[J].Pattern Recognition，2013，46(3)：834-844.

[2] LIU W R.Analyzing the degree of conflict among belief functions[J].Artificial Intelligence，2006，170(11)：909-924.

[3] SMETS P.Analyzing the combination of conflict belief functions[J].Information Fusion，2007，8(4)：387-412.

[4] 郭华伟，施文康，邓勇，等.证据冲突：丢弃，发现或化解?[J].系统工程与电子技术，2007，29(6)：890-898.

[5] YAGER R.On the dempster-shafer framework and new combination rule[J].Information Science，1987，41(2)：93-137.

[6] DUBOIS D，PRADE H.Representation and combination of uncertainty with belief functions and possibility of measures[J].Computational Intelligence，1998，4(2)：244-264.

[7] SMETS P.The combination of evidence in the transferable belief model[J].IEEE Transactions On Patten Analysis and Machine Intelligence，1990，12(5)：447-458.

[8] SMARANDACHE F，DEZERT J.Advances and applications of DSmT for information fusion[M].Rehoboth：American Research Press，2006.

[9] 邓勇，施文康.一种改进的证据推理组合规则[J].上海交通大学学报，2003，37(8)：1275-1278.

[10] 郭华伟，施文康，刘清坤，等.一种新的证据组合规则[J].上海交通大学学报，2006，40(11)：1895-1900.

[11] 王壮，胡卫东，郁文贤，等.基于均衡信度分配准则的冲突证据组合方法[J].电子学报，2001，29(12)：1852-1855.

[12] LEFEVRE E，COLOT O.A generic framework for resolving the conflict in the combination of belief structures[C].The 3rd International Conference on Information Fusion. Paris，France：IEEE，2000.

[13] VOORBARRK F.On the justification of Dempster’s rule of combination[J].Artificial Intelligence，1991，48(2)：171-197.