0 引言

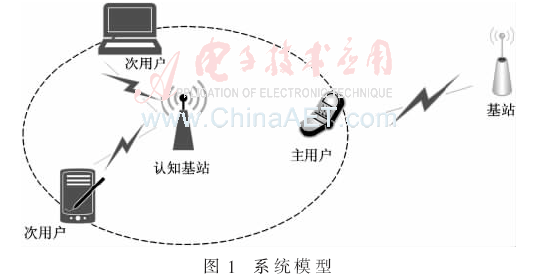
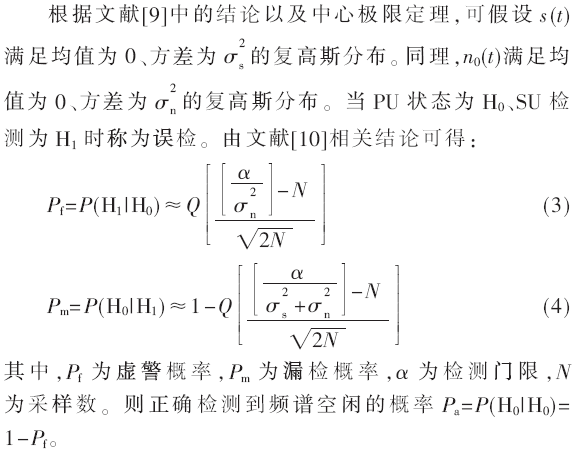
    无线通信业务的扩展对频谱资源的需求迅速增加，而适用于地面移动通信的授权频谱资源却是面临低效的使用^[1]。针对这一情况，通过感知技术让次用户(Secondary User，SU)获取空闲时频资源，并在主用户(Primary User，PU)无感的情况下进行频谱资源再利用的认知无线电技术因运而生^[2]。为了更高效地利用有限的频谱资源，现有文献广泛展开了针对业务特性、用户特性、信道特性进行认知无线电系统建模并分析系统性能和参数的研究。

    文献[3]针对非实时业务，利用带有优先级的强拆式排队模型描述SU的接入行为，得到了呼阻率、中断率、信道利用率等系统关键参数的解析结果。文献[4]使用盲源分离方法和隐马尔可夫模型对认知无线电系统的容量性能和检测概率等问题展开了讨论，并通过理论分析和仿真说明了二者之间的关系。文献[5]针对带有缓冲队列的主次用户协作认知无线电系统，利用马尔可夫链模型构建系统传输模型，并基于此模型对系统稳定性和容量性能进行分析。证明了文中的协作方式能够显著降低系统传输延时并提高系统的整体容量。文献[6]采用了马尔可夫模型集的方法，针对大量非相似非协作SU的复杂场景进行系统建模，并提出了该复杂场景下的系统容量分析方法，最后利用仿真对理论分析结果进行了验证。文献[7]使用时间连续马尔可夫链模型描述PU的出现特性，分析获得了PU占据信道的累计时间及分布概率。

    上述文献都引入马尔可夫链对认知系统进行建模，并且分别针对各自不同的系统参数与条件对系统性能进行了分析与仿真。认知无线电系统可以用频谱空闲、PU占用频谱、SU占用频谱、PU与SU共占频谱四种离散状态对整个系统的频谱使用情况进行描述。本文根据认知系统的状态转移特性，使用四状态连续时间马尔可夫链（Continuous-Time Markov Chain，CTMC)进行系统建模，在此基础上使用“流平衡”理论进行理论推导，获得各个状态平稳分布的闭式解，进一步综合分析系统检测概率、认知系统检测信号信噪比、认知系统容量、整体频谱利用率4项指标的相互影响以及对系统性能变化特性，最后通过数值仿真对分析结果进行验证。

1 系统模型

    考虑如图1所示系统模型，PU与SU分属不同系统，认知基站通过检测PU的无线信号，判断频谱是否空闲，进而确定认知系统是否进行信号传输。PU对于授权频谱拥有最高使用权，SU在使用频谱之前，需要判定频谱的占用情况，当频谱空闲时对频谱接入使用，若频谱被占用，则将到来的业务放入缓存中等待下次接入。频谱检测可以认为是一个二进制的检验问题，可以描述为：

其中，H₀表示接收端只接收到噪声时的情况，H₁表示接收端同时接收到信号和噪声的情况。n₀(t)表示接收到的噪声信号，s(t)表示接收到的PU信号。

2 次用户系统容量性能分析

    在认知系统中，PU拥有使用授权频谱的最高优先级，次用户在使用未授权频谱时需要先对频谱情况进行检测，仅当频谱空闲时才能够接入频谱。当SU占用频谱时，若PU接入频谱，二者将发生冲突，造成当次传输失败。又因为PU与SU接入和释放频谱的过程是两个独立的泊松过程^[11]，因此，可以建立PU优先的CTMC对SU和PU的行为过程进行建模分析。

2.1 主用户优先的连续时间马尔可夫模型

    假设PU和SU的服务请求服从参数为λ_p和λ_s的Poisson过程，而其占用频谱的时间分别服从参数为μ_p和μ_s的负指数分布，则系统的CTMC状态转移图如图2。

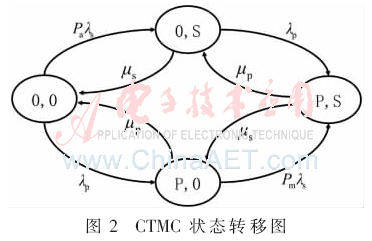
    其中，状态{0，0}表示频谱空闲，没有用户接入；状态{0，S}表示SU接入频谱，PU未接入频谱；状态{P，0}表示PU接入频谱，SU未接入频谱；状态{P，S}表示PU与SU都接入频谱，二者发生传输冲突。

    假设刚开始频谱处于空闲状态，则处于CTMC模型中的状态{0，0}。此时SU若有业务到来需要接入并且正确检测到频谱空闲状态，则开始占用频谱，CTMC状态跳转到{0，S}，跳转概率为P_aλ_s；若SU的业务传输完成，并且在传输过程中PU没有接入频谱，则从状态{0，S}跳转回状态{0，0}，跳转概率为μ_s。因为PU对授权频谱拥有绝对优先权，SU的存在对于PU而言是透明的，因此PU一旦有业务到来，立即接入频谱，此时若频谱处于空闲状态，则CTMC状态从{0，0}跳转到{P，0}，跳转概率为λ_p；若SU正处于接入状态，则CTMC状态从{0，S}跳转到{P，S}，跳转概率为λ_p；在状态{P，S}中，SU传输完成前，PU传输完成，则CTMC状态从{P，S}跳转到{0，S}，跳转概率为λ_p；若PU传输完成前，SU传输完成，释放频谱，则CTMC状态从{P，S}跳转到{P，0}，跳转概率为λ_s。在状态{P，0}中，若没有SU接入，则PU业务传输完成，CTMC状态从{P，0}跳转到{0，0}，跳转概率为μ_p；若SU有业务到达，但是对频谱的检测发生了漏检情况，则SU也会接入PU占用的频谱中，CTMC状态从{P，0}跳转到{P，S}，跳转概率为P_mλ_s。

2.2 容量性能分析

    从统计意义上说，认知系统追求最大系统容量，也就是更高效利用空闲频谱。系统各状态的平稳分布也能够反映不同系统的容量以及传输冲突的损失。根据上述CTMC模型，结合“流平衡”理论^[11]，能够得到如下方程：

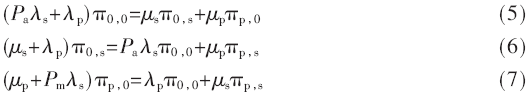
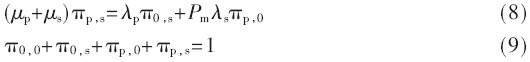
其中，π_a，a表示的是在系统状态{a，a}的平稳分布。上述方程组反映了认知系统和PU系统在各个状态的平稳分布和转移概率。通过对上述方程组进行求解可得各状态平稳分布：

    上述公式推出了认知系统和PU系统各种接入状态的平稳分布，正如前面所定义的，π_a，a表示的是系统出现在状态{a，a}的概率，在统计意义上，平稳分布能够等效于在某一状态的停留时间，因此认知系统的容量也就是其在状态{0，S}和状态{P，S}的平均容量，由此，可得认知系统总容量C_s为：

其中，W_s是认知系统所使用的频谱带宽，P_s表示认知系统发送功率，G_s表示信道衰落系数。P_sC_s/n₀即为认知系统的接收端所收信号的信噪比γ_s。

    从式(16)可以看出，认知系统的总容量受到多个因素影响。系统频谱带宽以及接收信号的信噪比直接决定了认知系统的实时容量性能。而CTMC状态的出现概率影响认知系统在统计意义上的容量性能。CTMC下{0，S}状态的平稳分布π_0，s不仅受到SU的业务接入参数影响，同时也与PU的业务强度相关。另外由式(3)和式(4)可知，认知系统的检测概率与接收端所收信号信噪比γ_s相关，并且检测概率也将对π_0，s的数值造成影响。下面通过数据仿真将各项参数的变化对认知系统容量造成的影响进行分析。

3 性能仿真与分析

    本节根据上述建模与理论分析，对各项参数的相互影响进行理论和数值仿真的对比分析。仿真条件设置如下：以VoIP服务作为PU业务参考^[12]，P_PU,H1=0.35，即PU出现占用频谱的概率为0.35，从CTMC中表现为π_p，0+π_p，s=0.35，检测概率设定为P_m=0.1。SU的接收信噪比为0 dB。

    从图3可以看出，理论曲线与仿真结果基本吻合。该仿真反映了SU不动的情况下，PU移动造成检测概率变化对于SU的系统容量的影响。图中显示在不同的接入强度下，随着检测信噪比的增加，认知系统的容量在(-10 dB，0 dB)的区间内都呈现出快速增加的趋势，但是在0 dB之后，容量不再随着信噪比的增加而提高，而是趋于平坦。相同的接入强度差值下，系统容量的变化幅度不同。在信噪比大于0 dB时，接入强度λ_s=10与λ_s=30的容量差值大约为0.25 bit/s/Hz，而接入强度λ_s=30与λ_s=50的容量差值大约为0.2 bit/s/Hz。同样的接入强度差值，却有不同的容量差值，造成这一情况的主要原因是随着接入强度的增加，SU业务到来时PU正在占用信道的概率将会增加，另外SU传输过程中PU接入造成传输冲突的概率也将提高。因此，提高SU用户的接入强度所获得的系统容量增益也将随着接入强度的增大而变小。

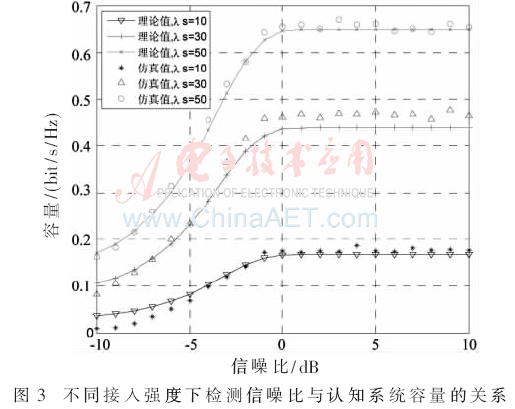
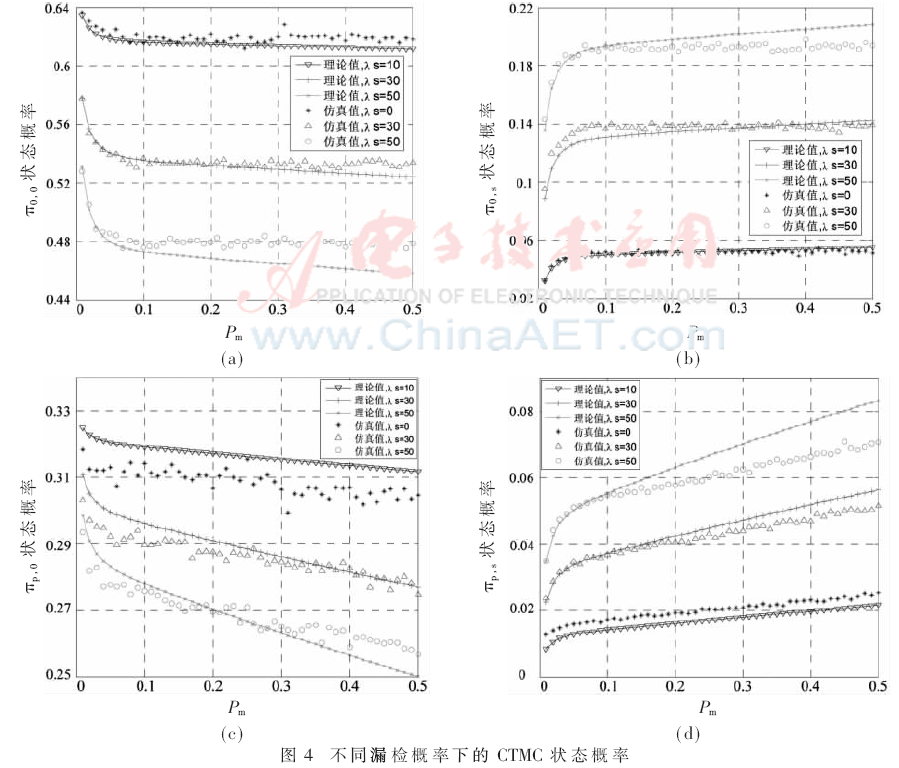
    图4显示了不同漏检概率下，各状态概率值的理论结果和数值仿真结果。从图中可以看出，数值仿真结果与理论分析结论基本吻合，因此证明了理论分析的合理性与有效性。从图4的四幅图片中可以看出，在P_m较小的条件下，各个状态的概率值都有一个明显的非线性变化区域，这一现象的原因在于漏检越小，则虚警越大，并且这一关系也是非线性的。而SU检测时，较高的虚警概率将显著降低其对空闲频谱的利用效率。因此，从图中可以看到，接入强度越大，低漏检概率下的非线性趋势也就越发明显。

4 总结

    本文根据认知系统的状态变化特点，引入连续时间马尔可夫模型对SU和PU的行为进行建模。利用“流平衡”理论构建状态转移方程，并推导获得不同状态平稳分布的闭式解。然后根据统计意义下各个状态的出现概率与占用时间的等效性，通过理论推导与数值仿真对接收信噪比与认知系统容量的变化关系进行了分析。本文的数学模型和分析结果不仅能够为认知系统的进一步优化与分析提供基础，也能够为应用系统的参数设计提供部分参考。

参考文献

[1] Federal Communications Commission.Notice of proposed rule making and order: Facilitating opportunities for flexible，efficient, and reliable spectrum use employing cognitive radio technologies[J].ET docket，2005(03-108)：73.

[2] HAYKIN S.Cognitive radio：brain-empowered wireless communications[J].Selected Areas in Communications，IEEE Journal on，2005，23(2)：201-220.

[3] 郭彩丽，曾志民，冯春燕，等.机会频谱接入系统的切换请求排队机制及性能分析[J].电子与信息学报，2009，31(6)：1505-1508.

[4] MUKHERJEE A，MAITI S，DATTA A.Spectrum sensing for cognitive radio using blind source separation and hidden markov model[C].Advanced Computing & Communication Technologies(ACCT)，2014 Fourth International Conference on.IEEE，2014：409-414.

[5] KAM C，KOMPELLA S，NGUYEN G D，et al.Cognitive cooperative random access for multicast：stability and throughput analysis[J].Control of Network System，IEEE Transactions on，2014，1(2)：135-144.

[6] LI X，XIONG C.Markov model bank for heterogenous cognitive radio networks with multiple dissimilar users and channels[C].Computing，Networking and Communications(ICNC)，2014 International Conference on.IEEE，2014：93-97.

[7] 岳新智，郭滨.基于纯不联系马尔可夫过程的频谱感知研究[J].吉林大学学报（信息科学版），2014，32(1)：29-35.

[8] COVER T M，THOMAS J A.Elements of information theory[M].John Wiley & Sons，2012.

[9] MA J，ZHOU X，LI G Y.Probability-based periodic spectrum sensing during secondary communication[J].Communications，IEEE Transactions on，2010，58(4)：1291-1301.

[10] 韩维佳，李建东，姚俊良，等.认知无线电中接入机会的建模与优化[J].西安电子科技大学学报(自然科学版)，2012，39(1)：1-6.

[11] WANG B，JI Z，LIU K J R，et al.Primary-prioritized Markov approach for dynamic spectrum allocation[J].Wireless Communications，IEEE Transactions on，2009，8(4)：1854-1865.

[12] HOVEN N，TANDRA R，SAHAI A.Some fundamental limits on cognitive radio[J].Wireless Foundations EECS，Univ.of California，Berkeley，2005.