0 引言

    稳定平台是指能够使被稳定对象在外来干扰作用下相对惯性空间保持方位不变，或在指令力矩作用下能按给定规律相对惯性空间转动的装置^[1]。

    风浪会影响海面航行的船只，使之摇摆。船载摄像机也受其影响而不稳定，导致被摄像目标偏移或丢失，因此摄像机必须架设在船用稳定平台上，通过平台的方位、俯仰和滚转三大驱动系统补偿舰船的扰动，使摄像机始终保持水平状态^[2]。

    典型频域校正控制方法能够保证系统在一定范围内相对稳定，但控制对象的精确模型难以获得，加之环境条件的变化将影响系统本身特性，因此基于固定校正环节的算法不能保证系统时刻具有最佳性能^[3-4]。特别是在船载设备中，当船体处于不同运动姿态时，平台重心改变，轴系之间摩擦力矩也随之改变，以上因素将导致控制对象的特性与固定校正时特性有所不同，因此，设计了一种带有摩擦补偿同时对参数不敏感的变结构控制方法，使系统具有良好性能。

1 稳定平台框架结构

    摄像控制平台是高精度和快速跟踪伺服系统，三轴稳定平台示意图如图1所示。

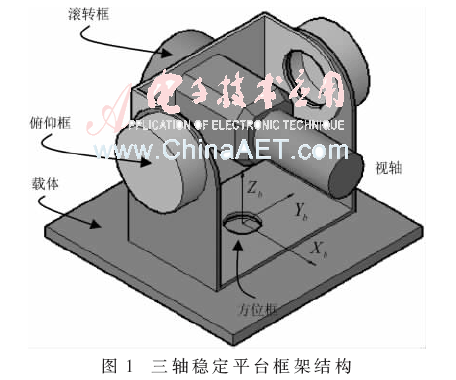
    为获得清晰视频图像，通常利用陀螺稳定摄像平台提供良好的空间隔离环境，装置采用机电框架结构实现^[5]。

    平台伺服系统包括方位、俯仰和滚转框架，三部分伺服结构基本相同，这里仅以一轴为例。伺服系统包含内外二环：速度反馈回路是内环，依靠速率陀螺仪测量角速度，电机将与之相反方向运行，确保摄像平面稳定；外位置反馈回路通过测得的加速度经过变换获得角位置信息。

    在此，设备采用惯性组合，即两个垂直安装的陀螺仪和加速度计组合，分别输出角速度和倾角信号。经过A/D转换，送到控制器，与伺服电机和其他部件共同组成闭环回路。系统框图如图2所示。

2 基于摩擦补偿的变结构控制建模与设计

    摩擦存在于所有的运动中，是影响系统低速性能的重要因素，它不但造成系统的稳态误差，而且会使系统运动产生爬行、振荡现象。为了减轻机械伺服系统中由摩擦环节引起的不利影响，该摄像稳定平台可采用变结构控制方法。

    由于变结构控制简单、有效、鲁棒性强，因此常被作为处理非线性系统不确定性和干扰的有效手段，一些学者已就观测器和动态补偿器等做了研究和应用，但摩擦是影响控制精度的一个重要因素。本文考虑系统摩擦特性，使之能更真实地反映所设计控制器的作用。

2.1 摩擦模型介绍

    平台机械结构的框架间具有较大摩擦死区，是系统低频段的主要非线性干扰。被控对象的非线性导致系统产生爬行、振动，传统的控制方法难以实现高精度控制。摩擦模型很多，这里采用较常见的Stribeck摩擦模型。

2.2 变结构控制方法建模

    变结构控制思路是采取一种非同一般的滑模控制，迫使系统状态变量沿着人为规定的轨迹滑动到期望点，它对于参数的不确定和外部扰动具有强烈的鲁棒性^[6]。给定的相轨迹与控制对象的参数和外部干扰变化不相关，只要符合滑模条件，就可确保系统稳定，并使其具有良好的动态性能^[7]。

    设r是期望位置信号，θ_o是实际输出角位置信号，ω_o是实际输出角速度信号。

    为使问题简单，电机的电枢电感被忽略。基于变结构控制的系统结构见图3。

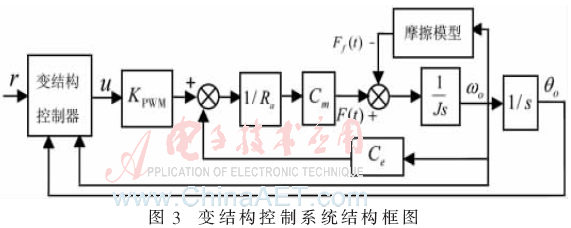
    图3可用差分方程描述如下：

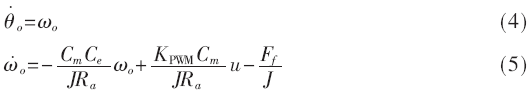
式中，u是控制项，C_m是电动机转矩系数，C_e为电机的反电动势系数，K_PWM 是脉冲宽度调制(Pulse Width Modulation，PWM)电路的系数，R_a为被电枢绕组的电阻，J是转动惯量总和。

    设x₁=θ_o，x₂=ω_o，将式(4)及式(5)写为状态方程形式：

    x₁和x₂分别代表平台角位置信号和角速度信号。

3 变结构控制平台仿真

    系统模型和摩擦模型的参数如下：

    R_a=7.77 Ω，C_m=6 Nm/A，J=0.6 kgm²，K_PWM=11，α=0.01，α₁=1.0，C_e=1.2 V/(radgs^-1)，F_m=20 Nm，F_c=15 Nm，c=30，k=5，ε=10。指令设为正弦信号r=0.1 sin2πt。

    首先采用PD控制^[8]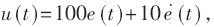，仿真结果见图4、图5。

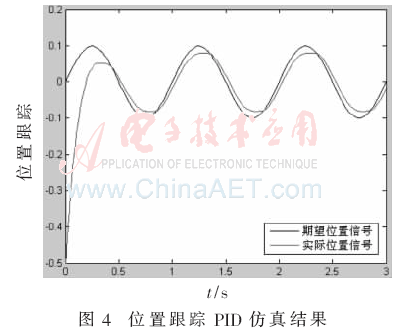
    仿真结果表明，因存在摩擦，位置跟踪出现“平顶”，而速度跟踪存在“死区”现象。 PID控制系统无法实现高精度跟踪和较强鲁棒性。

    再利用前面得到的变结构控制器，采用Simulink设计主程序，利用S-Function描述被控对象和控制器。仿真结果见图6～图8。

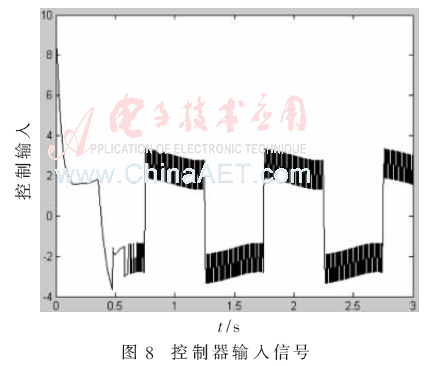
    从仿真结果可以看到，该控制可以消除摩擦造成的“平顶”和“死区”现象。平台系统快速跟踪期望信号，采用指数趋近律的变结构控制可以使系统逐渐稳定，并保持在滑模状态运动，动态效果良好。

4 结论

    在船载摄像稳定平台中，根据系统模型和参数不能精确以及平台运动包含摩擦和外部干扰的实际情况，设计基于指数趋近律的变结构控制。因为变结构控制是在动态过程中基于系统当前状态(诸如偏差和各阶导数)进行有目的地改变，迫使系统沿着预定滑动模态的轨迹运动。系统对参数和干扰不敏感，且不需要精确的动态模型。该控制可以克服摩擦影响，提高伺服系统跟踪精度。实验及仿真进一步表明，变结构控制优于传统PID控制，根据摩擦模型可以判断控制器的动态效果。这对控制器的设计和选择具有一定的指导意义。

参考文献

[1] HILKERT J M.Inertially stabilized platform technology concepts and principles[J].IEEE Contr.Syst.Mag，2008，28：26-46.

[2] AHMED J A，KHAN A A.Stabilized active camera tracking system[J].J Real-Time Image Proc，special issue 2012.

[3] COPOT C，ZHONG Y，LONESCU C M，et al.Tuning fractional PID controllers for a Steward platform based on frequency domain and artificial[J].Cent.Eur.J.Phys，2013，11：702-713.

[4] 姬伟，李奇.陀螺稳定平台视轴稳定系统自适应模糊PID控制[J].航空学报，2007，28(1)：191-195.

[5] 王玉辉.摄像稳定平台的陀螺自适应滤波器设计[J].计算机仿真，2014，31(9)：277-281.

[6] 何雅静，屈胜利，孟祥忠，等.两轮不平衡小车变结构控制抖振与鲁棒性研究[J].电子技术应用，2011，37(5)：130-133.

[7] 高为炳.变结构控制的理论及设计方法[M].北京：科学出版社，1996.

[8] 刘金琨.先进PID控制MATLAB仿真(第二版)[M].北京：电子工业出版社，2004.