摘 要： 在研究了Wu_Manber算法及其已有改进的基础上，在跳跃距离、匹配过程和并行处理三方面进行了综合改进。改进后的算法跳跃距离最大能达到m+1，有效减少匹配过程中的比较次数，最后充分利用现有的硬件处理能力，进行并行处理，避免模式串集合过度增加后算法效率的下降问题，提高超大文本串的扫描速度。

　　关键词： 多模式匹配；Wu_Manber算法

0 引言

　　多模式匹配问题可以描述为：P={p1， p2，...，pk}，是一个模式串的集合，其中任意一个模式串pi都是由字符表Σ中的字符所组成。T=t1，t2，...，tn是一个大文本串，ti属于Σ。求所有模式P在T中的所有出现。

　　多模式匹配算法一般是单模式匹配算法的推广。单模式匹配算法中经典并且效率较高的算法主要有BM（Boyer Moore）算法[1]和QS（Quick Search）算法[2]等。多模式串匹配算法中，Wu_Manber算法[3]是实际应用中平均性能最好的一个算法。QS算法是对BM算法的改进。而Wu_Manber算法是BM算法的多模式扩展。可以说，这几个算法的核心思想是一致的。

　　多模式匹配过程要获得高的效率，关键在于三个方面：一是尽可能多、尽可能远地进行跳跃，避免进入无效的匹配过程；二是在可能出现匹配时，尽量减少比较次数；三是综合利用现有硬件条件，进行并行运算。

　　在本文中，使用p[0..m-1]表示要匹配的模式串，长度为m。使用T=t[0..n-1]表示正文文本，长度为n。字符集以Σ表示，大小为σ。将匹配过程中P与T中长度为m的子串之间的一次比较称为一次尝试，并将T中的该子串称为当前匹配窗口，假设当前匹配窗口在T中的起始位置为k。

1 Wu_Manber算法

　　在多模式匹配中，随着模式串个数的增加，字符t[k+m]出现在各模式串尾端的概率相应增加，因而能达到的平均跳跃距离随之变小，BM或QS算法的跳跃效果在多模式串的情况下被极大地削弱。Wu_Manber 算法利用块字符扩展了不良字符的跳跃效果，同时用散列表来筛选匹配阶段应进行匹配的候选模式串，减少算法匹配时间。在每次匹配尝试中，一次考察一“块”，即连续B个字符。根据这B个字符所组成的块的匹配情况来决定跳跃距离。通常模式数量少的时候取B=2，模式数量大的时候取B=3。

　　Wu_Manber算法同样分为两个处理阶段。预处理阶段将建立三个表格：SHIFT表、HASH表和PREFIX表。SHIFT表中存储字符集中所有块字符的跳跃距离。HASH 表用来指出可能匹配的所有候选模式串。PREFIX 表用来过滤候选模式串。

　　取所有模式串长度的最小值为m，只考虑所有模式串的前m个字符。假设当前匹配窗口的最后B个字符组成不良字符块X：

　　⑴X在所有模式串中不出现，则跳跃距离为m-B+1，即SHIFT[X]=m-B+1。

　　⑵X在部分模式串中出现，则跳跃距离为X在所有模式串中的最右出现到X的距离。

　　如果X是良好字符块，则SHIFT[X]＝0，进入精确匹配过程。HASH[X]指向所有以X结尾的模式串列表，依次访问这些可能匹配的候选模式串，如果模式串的前缀与PREFIX表不符合，则跳过；否则比较该模式串中的每个字符以决定是否出现一个完全匹配(此时的比较不再限于模式串的前m个字符，而是完整的模式串)。

　　以上的讨论中，SHIFT[X]和HASH[X]指的是先将X散列，得到一个整数值，再用这个整数值作索引，查询SHIFT表和HASH表。

　　Wu_ Manber算法的时间复杂度在最好的情况下能达到O(B×n/m)。

2 对Wu_Manber算法的改进

　　2.1 对跳跃距离的改进一

　　2.1.1 精确的不良字符块跳跃距离

　　首先研究不良字符块X在所有模式串中不出现时，其跳跃距离是否只能达到m-B+1。

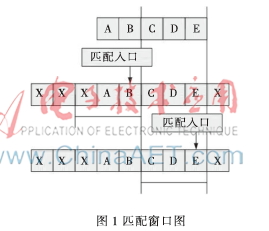
　　如图1所示，假设“ABCDE”为模式串集中长度最小的模式，此时匹配窗口的块字符为“XAB”，虽然“XAB”是个不良字符块，但是它的后缀“AB”是模式“ABCDE”的前缀，此时如果将匹配窗口移动m=5，那么就会漏掉一次正确的匹配。长度为B的不良字符块，至多它的长度为B-1的后缀可能在模式串中出现。因此安全的跳跃距离为m-(B-1)=m-B+1=3。但是这种情况的出现次数相对于匹配中遇到的大多数不良字符块转移来说所占比例非常少，它减少了大多数情况下的跳跃距离，因此可以引入精确的不良字符跳跃表Shift[ ]，其最大跳跃距离可以达到m。

　　精确的Shift[ ]计算过程：

　　⑴ 用m填写Shift[ ]表；

　　⑵for (i = 1 ；i < B ；i ++ )

　　{

　　对所有Bc ∈{ suffix(Bc，i) = prefix(pattern，i) }

　　Shift [Bc ] = m - i ；

　　}

　　⑶For 每一个关键词

　　{

　　For 当前关键词中的每一个块字符

　　计算Shift[ Bc ] ；

　　}

　　2.1.2 弱化的良好字符块跳跃距离

　　Wu_Manber算法中没有使用BM算法中使用的良好字符跳跃方法，因此无论当前良好字符块的匹配结果如何，跳跃距离都固定为1。为此引入一种弱化了的良好字符块跳跃表GBSShift[ ]来改进这一问题。该表记录了每一个模式串的长度为B的后缀(最后一个块字符)在所有模式串中的所有非后缀出现位置与后缀的距离的最小值。这样，在匹配失败后，其跳跃距离很可能大于1。

　　实际试验证明了在附加微小的预处理时间(约为原预处理时间的10%)后，以上两种改进能够有效地降低比较次数，从而减少了对整个文本数据的扫描时间(约为原算法扫描时间的85%~92%) 。

　　2.2 对跳跃距离的改进二

　　结合Q S算法的思想，忽略当前匹配窗口的信息，不管匹配是否成功，直接使用字符块t[m-B+1..m]来确定跳跃距离。跳跃距离至少为1，最大为m-B+2。但这样做的话，跳跃表就无法用来判断当前窗口是否存在可能匹配了(原算法跳跃距离为0表明存在可能匹配，应该进入精确匹配过程)。根据QS算法的特点，其匹配顺序没有要求，因此可以查看各模式串的前B个字符(前缀)与当前窗口的前缀是否匹配。为此需要增加一个表Head [ ]，记录各模式串前缀的信息。Shift表记录的是若当前文本与所有模式的前缀不同时， 数据指针向后跳跃距离。

　　Shift [ ]表计算方法为：

　　⑴ 用m填写Shift [ ]表；

　　⑵For 每一个模式串

　　{ //对当前模式串中的每一个块字符， 这里B = 2，计算跳跃距离；

　　for ( i= 0； i< m - 1； i+ + )

　　{

　　Hash = hashBlock (pattern+ i) ；

　　if (Shift[hash]> = m - 1- i)

　　Shift[hash]= m - 1- i；

　　}

　　}

　　Head 表计算如下：

　　⑴ 用 0 预置 Head[ ]表；

　　⑵For 每一个模式串

　　{

　　hash = hashBlock (pattern) ；

　　Head[hash ] = 1；

　　}

　　实验结果显示， 在最小模式长度较小时，当 m<9时，改进后的算法比原算法性能显著提高，用于英文文本时平均提高 8%~20%，用于中文文本时平均提高约15%~30%；当最小模式长度较大时， 改进后的算法性能与原算法基本相同。

　　2.3 对跳跃距离的综合改进

　　以2.2节为基础，结合2.1节的思想，计算其不良字符块的精确跳跃距离，将使得最大跳跃距离能够达到m+1。另外，同样引入2.1节所使用的弱化的良好字符块跳跃表。这样，改进后的算法思想为：在当前匹配窗口中，如果根据Head[ ]表发现不可能出现匹配，则使用精确的不良字符块跳跃表直接向右移动窗口，其最大距离可达m+1，否则，进入精确匹配过程，比较顺序为从右向左。如果找到匹配则输出，再次采用精确的不良字符块跳跃表直接向右移动窗口，否则比较不良字符块跳跃表和弱化的良好字符块跳跃表，选取较大值作为窗口的跳跃距离。

　　2.4 匹配过程改进一

　　进入精确匹配过程后，Wu_Manber 算法对HASH[X]指向的候选模式串列表进行逐个比较。如果模式串pj和pk都匹配成功，则pj是pk的后缀或者反之。称存在一个模式是其他模式的后缀的一组模式为后缀模式。例如模式this、his、is，如果没有后缀模式，就不可能有两个模式串同时匹配成功，所以一旦某个模式串匹配成功，就可以提前结束循环，根据跳跃表移动匹配窗口到下一个位置。

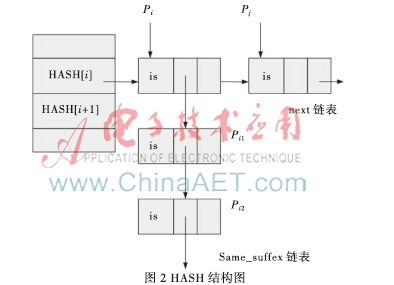
　　改进后的HASH数据结构增加了 same_suffix域，如图2。后缀处理算法把后缀模式的模式使用same_suffix域链接起来，这样在HASH表的next链表中的模式就不存在后缀模式。图2中，Pi为is，Pi1为his，Pi2为this，Pi、Pi1、Pi2构成一个后缀模式，其中Pi是其他模式公共后缀；通过Pi的 same_suffix链表链接Pi1、Pi2。

　　改进后算法效率在模式的各个规模上都有明显的提高，提高幅度达到8%~15%，说明后缀模式处理能够比较稳定、有效地提高算法的运行效率。

　　2.5 匹配过程改进二

　　由于 CPU进行一次8位的字符比较与进行一次机器字长的整数比较所花费的时间完全相同，因此完全可以一次比较4个字符（32位CPU），以此提高效率。

　　2.6 其他改进

　　算法在匹配过程中的最大“跳跃” 距离是由所有模式串中最短的模式串长度 m决定的。所以如果最小模式串的长度为1或2，则最大跳跃距离将非常有限，会大大降低算法的性能。

　　实验得出的数据为：当m=1时，算法所用时间是其他情况下的7~10倍；m=2时，算法所用时间是其他情况下的4~9倍。针对这个问题，可以将模式串集一分为二，长度小于等于2的为一组，其他的为另一组。将算法在这两个模式串子集上分别运行，最后得到总结果。

　　改进后的Wu_Manber算法性能有明显提高。特别是对于英文匹配，在单字节模式串出现个数较少时，匹配速度较原来提高了 5~8倍。考虑到现实中，单字节(单汉字)模式串出现个数较少，所以这种改进还是具有一定的实用价值。

　　2.7 并行处理

　　现在随着CPU内核数的增多，在算法实现时应充分利用其并行处理能力。

　　2.5节提出的问题和解决方法完全可以用两个线程或进程同时并行处理。不仅如此，应将模式串集合合理分组，用多个线程或进程并行处理，每个线程或进程负责处理一个模式串子集，降低模式串集合过度增加后算法效率的下降。

　　大文本则切成数段，每段之间有一定的重合，保证不遗漏可能匹配，采用多个线程或进程同时处理，每个线程或进程负责处理一段文本，这样在线程数不超过CPU核心数的前提下，超大文本串的扫描速度将以近似线性增加。

3 结束语

　　多模式匹配算法是一个基础算法，有许多重要应用场合，对其进行深入研究和试验具有重要意义。通过对Wu_Manber算法的仔细研究，在算法实现过程中对算法作出了多方面的改进，在实际应用中，取得了良好的效果。

参考文献

　　[1] Boyer R S，Moore J S. A fast string searching algorithm[J]. Communications of the ACM，1977(20)：762-772.

　　[2] SUNDAY D M. A very fast substring search algorithm[J]. Communications of the ACM，1990, 33(8)：132-142.

　　[3] Sun Wu，Manber U. A fast algorithm for multi pattern searching [R]. Technical Report TR94217，University of Arizona at Tuscon， 1994.

　　[4] 杨东红，徐恪，崔勇.改进的Wu-Manber 多模式串匹配算法[J]. 清华大学学报 (自然科学版)，2006，46(14)：109-112.

　　[5] 李雪梅，代六玲，童新海，等.对 QS串匹配算法的一种改进[J]. 计算机应用与软件，2006，23(3)：55-57.

　　[6] 张鑫，谭建龙，程学旗.一种改进的Wu_Manber 多关键词匹配算法[J]. 计算机应用，2003，23(7)：544-549.

　　[7] 孙晓山，王强，关毅，等.一种改进的 Wu_Manber 多模式匹配算法及应用[J]. 中文信息学报，2006,20(2)：47-53.

　　[8] 陈瑜、陈国龙. Wu_Manber算法性能分析及其改进[J]. 计算机科学，2006，33(16)：207-029.