摘 要： 根据LuGre摩擦模型辨识理论，以伺服电机驱动轴与伺服电机内部的摩擦模拟机器人关节摩擦，建立LuGre摩擦模型。对伺服电机做基于固高卡的模拟量控制，通过C++编程，从编码器中读取角度、转速值、加速度值。正转速度和对应的驱动力矩，以及反转速度和对应的驱动力矩，分别构成静态参数辨识的两组数据。位移、速度、加速度和驱动力矩构成动态参数辨识数据。在Matlab中编写粒子群算法辨识程序，对以上数据进行处理，最终得到LuGre模型的6个参数的辨识值。
关键词： LuGre；摩擦模型；模拟量控制；粒子群算法
0 引言
机器人的控制性能与动力学模型建立的精确度密切相关。由于摩擦而产生的关节阻尼是存在于机器人机构各构件之间的主要耗能因素，通常看成干摩擦阻尼。对于干摩擦阻尼的描述，近几十年来提出了许多数学模型，其中，LuGre摩擦模型全面而简洁地描述了摩擦力的动静态特性，受到了很大的重视。
LuGre摩擦模型将微观下接触表面看成是大量的具有随机行为的弹性鬃毛，其数学描述为：
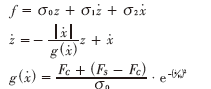
其中，参数Fc，Fs ，Vs，σ2为静态摩擦参数，用来描述运动副接触面间发生滑动后的摩擦现象,而参数σ0、σ1为动态摩擦参数，用来描述运动副处于粘着状态下(即处于预滑动摩擦区域)的摩擦力与预滑动之间的关系。这6个参数可精确诠释摩擦力粘滑运动、摩擦滞后、预滑动位移、稳态振荡环等。
1 国内外研究现状
参考文献[1]和参考文献[2]分别采用遗传算法和粒子群算法对LuGre模型分静力参数及动力参数两步来实现参数的辨识。但是在辨识动力参数时，上述两文献利用带有PID控制器稳态振荡环辨识参数，存在实现振荡环需根据经验来调节PID控制的比例因子﹑微分因子以及积分因子的问题。
参考文献[3]利用改进遗传算法和粒子群算法对摩擦力LuGre模型的6个参数进行辨识。静力参数辨识方法同参考文献[1-2]，但在动力参数辨识时采用传感器输出的位移或加速度以及输出的控制剪切力直接进行参数辨识，在辨识过程中把控制剪切力作为目标逼近值，进而辨识出两个动力参数。此动力参数辨识过程与参考文献[1-2]的精度和效率相比具有更快的参数辨识速度和更好的鲁棒性能，同时避免了PID选取过程。参考文献[4]提供了具体程序编制，但没有开展实验研究工作。本文的目的是通过实验研究来获取摩擦参数。
2 单自由度机器人转动关节LuGre摩擦模型的建立
由参考文献[4]可知，进行静态参数辨识时，需要多组机器人转动关节在已知的驱动力矩作用下对应的正转速度值和反转速度值。进行动态参数辨识时，需要多组机器人转动关节在已知的驱动力矩作用下对应的位移、转速、加速度值。在搭建实验平台时，电机和卷筒构成单自由度系统，电机输出轴与电机固定本体构成一个转动关节，卷筒通过联轴器与电机输出轴相连，模拟机器人转动关节的运动，建立机器人转动关节LuGre摩擦模型。上述静、动态参数辨识所需要的数据即是伺服电机在已知驱动力矩作用下的相关数据。
建立LuGre摩擦模型后，加以辅助和控制装置。该实验平台主要包括机架、伺服电机与驱动器、运动控制卡以及用于控制的上位机等，如图1所示。本实验选用的伺服电机为松下A5系列的MHMD082G1V，功率为750 W，驱动器型号为MCDHT3520。
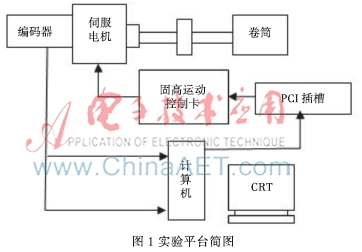
关节所受的电机驱动力（或力矩）与关节所受的摩擦力之间的关系可用下面的微分方程表示：
其中， (J1+J2 )是电机和绞盘的转动惯量之和；x是电机输出轴的转角；u是关节所受的电机驱动力矩；F是摩擦力矩。
当系统运动处于稳态，
取常数时，
，由前文LuGre摩擦模型的数学描述得：
则稳态运动时摩擦力F为：
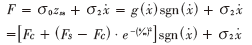
3 LuGre摩擦模型参数辨识理论
3.1 静态参数辨识理论
![$4SZ2WI]0NKN74H_K)SIQ`X.png](http://files.chinaaet.com/images/2015/08/29/6357645703207200001940137.png "$4SZ2WI]0NKN74H_K)SIQ`X.png")
目标函数定义为：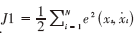
，辨识静态参数即是最小化目标函数J1。
3.2 动态参数辨识理论
在动态参数辨识时利用伺服系统输出的位移（或加速度）以及输出的控制剪切力直接进行参数辨识，在辨识过程中把控制剪切力作为目标逼近值。假定需要辨识的动态参数
，辨识误差定义为：
![_~N}PQ(BYKF4]O08)O1GXIQ.png](http://files.chinaaet.com/images/2015/08/29/6357645719102200005000768.png "_~N}PQ(BYKF4]O08)O1GXIQ.png")
其中，u(ti)为伺服系统控制剪切力，u(xd,ti)为模型参数系统辨识输出控制力。由上式可得：
![D{1V6VV_]DJYXTZJBM[(8Q4.png](http://files.chinaaet.com/images/2015/08/29/6357645720252500003617131.png "D{1V6VV_]DJYXTZJBM[(8Q4.png")
在预滑动区，质量块所受的外力F小于最大临界静摩擦力，可以近似认为鬃毛的平均变形等于质量块的位移，即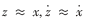
，此时系统摩擦力F简化为:
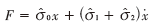
目标函数定义为：
，辨识动态参数即是最小化目标函数J2。
3.3 粒子群算法（PSO）参数设置及程序编写
PSO 参数包括: 种群大小PopSize 、种群维数Dim、惯性权重ω ,学习因子c1和c2，最大速度Vmax、最大迭代数Gmax、种群搜索空间等。
本文采用的参数值为：种群大小PopSize=35，种群维数Dim=4，采用Shi Yuhui等提出的方法[5]，将ω设置为从0.9线性下降至0.4，使得PSO能更好控制全局搜索能力和局部搜索能力，加快收敛速度，提高算法的性能。学习因子一般设置是c1=c2∈[1,2.5]，设置学习因子c1=c2=2。最大速度Vmax=100，最大迭代数Gmax=1 500，参数种群搜索空间设置为Fc=[0,100]，Fs=[0,100], Vs=[0,0.1], σ2=[0,50]。
在正确设置算法参数的基础上，以J1和J2分别作为静态和动态参数辨识程序的目标函数，进行Matlab粒子群优化算法程序的编写。
4 实验研究过程
4.1 参数调整
模拟量控制是向伺服单元输入模拟量指令形式的力矩指令，利用与输入电压成正比的力矩来控制伺服电机运行的方法。硬件连接完成后，开始调试电机并对电机参数进行设定。
首先选择模拟量控制（模拟量指令）的控制方式并调整输入增益。然后调整指令偏置量，用以消除模拟量指令为0 V时伺服电机可能的微速旋转带来的指令电压的微小偏差。最后对电机转速进行限制，以防止电机转速过大而产生不必要的振动。
4.2 控制程序的编写
本实验采用固高卡GTS-800-PV来控制电机运动，需要基于固高公司提供的运动控制器的动态链接库来使用，利用Visual C++编制位置、转速、加速度测量程序，其中读取编码器位置、转速、加速度的命令分别为：GT_GetAxisEncPos、GT_GetAxisEncVel、GT_GetAxisEncAcc。
4.3 参数辨识实验
辨识参数时，在测量程序界面中依次输入35个驱动力矩，从电机使能开始直至电机转速趋于稳态之后，每隔10 ms读取一次对应的正转速度值和反转速度值、位置值、加速度值。其中35个驱动力矩、正转稳态速度、反转稳态速度构成静态参数辨识数据，35个驱动力矩及其对应的电机转速未达到稳态时的转速、位置、加速度，构成动态参数辨识数据。
4.4 数据处理
程序中读取的伺服电机编码器的位置值、转速值、加速度值均为脉冲值（单位为Pulse），根据换算关系，将它们的单位转换为rad、rad/min、rad/s2。
5 实验结果及验证
LuGre模型共有6个参数Fc，Fs ，Vs，σ2，σ0，σ1。其中Fc，Fs ，Vs，σ2 4个参数在电机正转和反转时有不同的数值，正转时，上述4个参数值表示为F+c，F+s，V+s，σ+2，反转时表示为F-c，F-s，V-s，σ-2，辨识结果如表1所示。
为验证实验结果的准确性，根据辨识结果，分别对35组驱动力矩下的伺服电机转速变化过程进行推导，并与实测转速作比较。仅以驱动力矩为0.069 6 Nmissing image filem时，伺服电机的转速变化过程为例进行说明，而其他驱动力矩下具有相似结论。
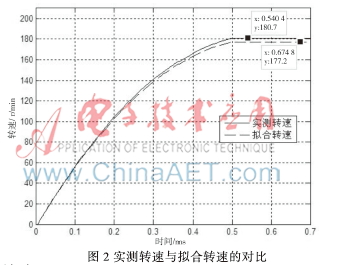
如图2所示，在伺服电机转动加速阶段，即本文中LuGre摩擦模型处于预滑动区域时，实测转速与拟合转速基本吻合，仅在较高转速时，有少量误差，从而可以证明本文辨识的LuGre摩擦模型动态参数辨识结果的准确性。在伺服电机匀速转动阶段，即本文中LuGre摩擦模型接触面间发生滑动后，实测转速稳定在180.7 r/min，拟合转速稳定在177.2 r/min，绝对误差为3 r/min，相对误差为1.6%，可以证明本文静态参数辨识结果的准确性。
6 结论
本文在辨识LuGre摩擦模型参数时，以伺服电机驱动轴与电机内部的摩擦模拟机器人关机转动摩擦，建立LuGre摩擦模型。对伺服电机做基于固高卡的模拟量控制，通过C++编程，从编码器中读取相关数据。在Matlab中编写粒子群算法辨识程序，对以上数据进行处理，最终得到LuGre模型的6个参数的辨识值。通过对实验结果的验证，说明辨识结果是比较准确的。实验中的误差可能是由转速较高时试验台的机械振动造成的。
参考文献
[1] Liu Deping. Genetic algorithms based parameter identification for nonlinear mechanical servo systems[C]. 2006 1st IEEE Conference on Industrial Electronics and Applications, 2006: 1-5.
[2] ZHANG Wenjing. Parameter identification of LuGre friction model in servo system based on improved particle swarm optimization algorithm[C]. Proceedings of the 26th Chinese Control Conference, 2007: 135-139.
[3] 孙洪鑫，王修勇，陈政清.辩识 LuGre 摩擦模型参数的两 种智能算法[C].第五届全国电磁流变液及其应用学术会议论文集，长沙，2008.
[4] Zheng Yaqing. Parameter identification of LuGre friction model for robot joints[C]. Proceedings of the 3rd International Conference on Manufacturing Science and Engineering (ICMSE 2012), Xiamen, China, 2012:27-29.
[5] SHI Yuhui, Eberhart R. A modified particle swarm optimizer[C]. In: IEEE Word Congress on Computational Intelligence,1998:69-73.