摘 要： 子空间理论中被用于奇异值分解或特征值分解的自相关矩阵,通常可表示为接收向量与其自身转置的乘积。提出了自相关矩阵的新型构造算法。该算法构造的自相关矩阵，特征值分解后其对噪声不敏感，克服了常规子空间方法的弱点。仿真试验表明，该方法应用在高噪声、低信噪比的实际通信环境下，特征值不会被噪声湮没，从根本上解决了传统子空间分辨率不足的问题。同时，仿真表明，该方法对于多用户扩频信号同样适用，可解决多用户扩频信号的码元分离问题，其计算结果与理论计算一致，验证了算法的正确性。
关键词： 子空间理论；相关矩阵；特征值分解；直序列扩频
0 引言
基于特征值分解（EVD）和基于奇异值分解（SVD）的子空间算法是近年来研究的热门方向。其在信号处理方面，如信号的频谱估计、阵列传感器数据估计和其他参数估计[1]等方面越来越受到广泛重视。但上述研究都是针对普通高信噪比情况下的调制信号而言，对于噪声环境中的扩频后的直扩信号罕有研究，对此，本文改进了子空间算法的分解矩阵——相关矩阵，对含噪情况下的直扩信号的分解算法做出了研究。
子空间[2]的相关矩阵（这里用R表示）可以用如下公式表示：
![]_XQP9)SK@_`SE}UIO0T)2I.png](http://files.chinaaet.com/images/2015/08/29/6357646658376200001385372.png "]_XQP9)SK@_`SE}UIO0T)2I.png")
其中yi代表第i个采样窗口内的采样点数（共M个采样点）；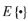
代表N个窗口内所有数据的平均值。
从上式可以看出，特征值的大小取决于信噪比而与统计窗口累计次数的多少并无关联。由此可以得出结论，传统子空间方法[3-4]，仅仅依靠增加统计窗口个数是无法解决提取信号特征值[5]，每个窗口如果都是处于较低信噪比的条件下，信号特征值仍然会湮没在噪声中。
区别于传统子空间方法，本文提出的重构方法，对R的建立不再采用missing image file的方式，而改用累乘的方法，即采样后的一段数据，各个窗口累乘，从而构造出新的相关矩阵。下文简称该方法为累乘算法（Matrix Multiplication based Subspace，MMS）。
该算法构造的新型矩阵具备如下特点：
（1）保留传统子空间方法构造矩阵的特性（在信号特征值与信噪比函数之间建立联系）。
（2）分解后的信号特征值大小与累计窗口数量相关。即信号特征值既是信噪比（SNR）ρ的函数也是累积窗口分段数K的函数。
（3）分析窗口数量越多，信号特征值增长越快，而噪声特征值几乎不随分析窗口的数量增长而增长。当累计窗口数量达到一定程度时，就能明显区分出信号特征值与噪声特征值。
文中最后将该算法构造的相关矩阵用矩阵特征值分解后得到新的特性，并将直扩信号作为算法的输入信号源，最终成功提取出多用户直扩信号码型。
1 直序列扩频信号数学模型
直序列扩频是将一个较窄的用户信号，通过直接相乘，使其变成一种宽带、高速率的码元信号。由于信号速率提高，从频域上看，其占用的带宽相应也变宽。
对本文使用到的各种数学符号作如下定义：
missing image file :用户扩频序列；
P:序列位数（长度）；
Ts: 符号周期；
Te: 采样周期；
Tc:码片周期(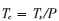
)；
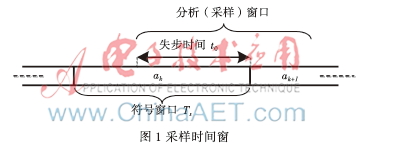
t0: 失步时间（采样窗口与实际的符号起止窗口时间差），如图1所示；
h(t):信号传输过程中所有信号畸变带来的影响总和，也可以理解为传输链中发射端滤波器、信道滤波器、接收端滤波器和其他信道畸变影响带来失真的卷积,表示如下：
missing image file：h(t)的矢量表示；
s(t): 扩频信号经接收机接收、解调后的基带信号:
n(t)：噪声；
σ2: 噪声方差;
y(t)=s(t)+n(t): 接收机解调输出含噪信号。
对上述变量和以下要推导的公式，需做如下限定：
（1） 扩频前用户基带信号ak在较长期限内“+1”、“-1”数量大体相等，均值为零；
（2）n(t)为与信号ak相互独立的（完全不相关的）高斯型白噪声；
（3）通过参考文献[6-7]，已经获取到该扩频信号的一些参数，如射频载波频率f0、符号周期Ts、码片周期Tc等。
对于假设（3），使用循环谱相关方法能够在极低SNR下计算出码片周期Tc和载波频率f0。一旦f0可得，可以设计相应下变频接收机，通过NCO产生f0频率，对射频信号f0进行相乘，从而下变频到基带。
若Tc已知，为了后续计算的简便，可将仿真采样周期Te直接设置成Tc，但这样仅仅为了计算方便，并非必要，即Tc可不知。
同样，采用倒谱技术能估计出扩频信号的符号周期Ts，将采样窗口周期设置为Ts。
2 累乘算法
按照上节所述，每个采样窗口时长为Ts，每个窗口内再分为K段，K段内又包含N个独立计算窗口，每段单独计算自相关。将K个自相关矩阵相乘，得到新算法后的带分解矩阵：
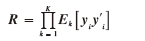
式中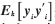
表示第k个N组窗口的均值；yi表示k段第i个窗口中采样序列。yi为列矢量。
按照上述理论，采样窗口周期设置为符号周期，单个采样周期内应该横跨两个符号，其中一个符号为ak，保持时间为t0（t0为失步时间，未知）；第二个符号表示为 ak+1，保持时间为整个符号周期减去上一个符号的保持周期(Ts-t0)。由于单个采样周期内存在两个符号，对该采样周期内的相关矩阵分解后，将呈现两个较大特征值，该特征值分别表示上述两个符号，而其他特征值均为噪声特征值：
![{P)%K7IX6I1K}22]7H$A2%G.png](http://files.chinaaet.com/images/2015/08/29/6357646702364600006359573.png "{P)%K7IX6I1K}22]7H$A2%G.png")
根据式（3），有：
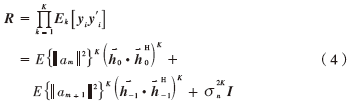
其中I为单位矩阵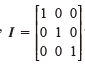
。由式（4）可以得出：矩阵
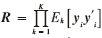中存在两个较大的特征值，每个值对应特征矢量为missing image file/missing image file与系数的乘积。
根据如下定义，可改写式（4），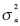
为基带符号的方差，定义：
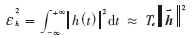
定义![5JUCE)KPOOVG}]917R{T46K.png](http://files.chinaaet.com/images/2015/08/29/6357646789219500002607059.png "5JUCE)KPOOVG}]917R{T46K.png")
如下：
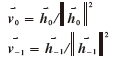
式（4）可改写为式（5）：
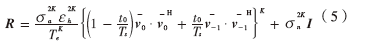
扩频后的信号方差可表示为：
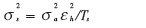
信噪比不直接采用信号比噪声，也不采用dB为单位的对数表达式，定义如下：
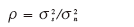
式（5）可改写为：
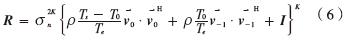
对矩阵（6）进行特征值分解，R的特征值中λ1、 λ2为上述表达符号矢量的两个较大特征值（信号特征值），其他特征值λi(i≥3)则可称为噪声特征值，由系统中的各类噪声引起。
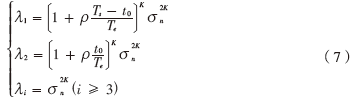
根据式（7），使用新型累乘构造方法，λ1、λ2不仅与信噪比ρ有关，同时也与分段数量K相关（即λ1、 λ2是ρ和K的函数）。
比较传统子空间相关函数构造方法：
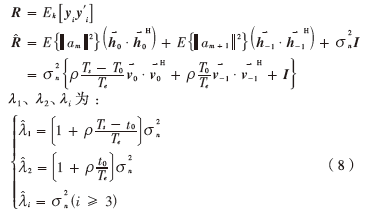
从式(8)可以得到，传统方法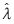
仅是信噪比ρ的函数,而与参与计算的窗口数量没有关系,窗口数量的提升不会改善信号特征值的分辨率。
式（7）、式（8）之间关系为：
式（9）按级数序列展开公式简化后得到：
为了进一步简化，这里假设：
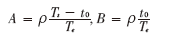
根据式（10），得到新算法特征值 λ1、λ2和λi之间的关系：
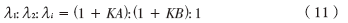
根据式（8），得到传统算法特征值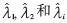
之间关系：
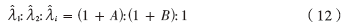
比较式（11）、式（12），低信噪比条件下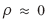
，根据定义
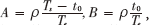，此时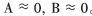 
得出结论：使用传统自相关算法构造的矩阵，分解后得到的结果不能从噪声特征值
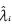中有效地分辨出信号特征值
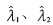。而采用MMS累计得到的相关矩阵，分解后由于K为一个大的正整数，能有效增加λ1、λ2与其他特征值λi之间的差异。
3 实验结果
考虑到计算量的问题，在验证该算法的有效性时，文中使用自相关、互相关性非常好的Gold码作为扩频序列，码长设为63，调制类型设为QPSK (Quaternary Phase Shift Keying)，信噪比设为SNR=-30 dB (按照如上定义，ρ=0.001)，采用K×N=10 000个分析窗口，对算法进行验证。
采样周期Te=Tc=Ts/P，采样窗口周期设为Ts，为了方便计算，信道内没有多径干扰，失步系数设定为T0/Ts =0.4，失步时间t0原则上未知，但可通过式（10）得出。
按照上述参数设置，最终分解后的特征值：
missing image file
missing image file比例关系接近1:1:1，如图2所示，信号特征值完全湮没在噪声特征值的波动之中。图2与式（13）中的理论计算相吻合，此时不能独立分离出信号特征值。
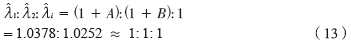
采用新算法MMS后，设定K=8, N=1 250，同样10 000个窗口条件下的仿真结果，如图3所示。表明missing image file之间比例关系：
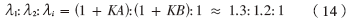
采用新算法后，可以明显发现λ1、λ2受K的影响，能明显分辨出信号特征值λ1、λ2与噪声特征值λi之间的差异。
同样，在不改变总窗口数量10 000的条件下，调整分段数，使K=20, N=500，信号特征值与噪声特征值比例关系理论上应为：
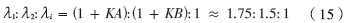
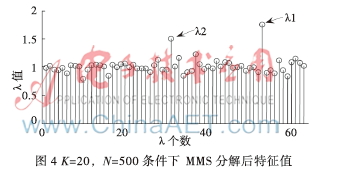
图4证明了这一理论推导。同理，比较图3、图4，随着K的增加，信号特征值λ1、λ2与噪声特征值λi的差异越来越明显。但总窗口数K×N一直为10 000，数量并未增加。K的增加导致每段内窗口数N的减小；样本数N的减小导致噪声对待分解矩阵R的影响增大。每个分段求出的相关矩阵差异较大，所以累乘方法求出的信号特征值的均方差波动比传统算法大。为了克服这一缺点，MMS算法适用于存在足够多分析窗口(即样本数足够多)的情况下，此时N和K都能取得一个较大的数值，N的增大可减小每个相关矩阵的均方差波动，K的增大可提高信号特征值分辨率。
将信号特征值λ1、λ2代表的特征矢量组合，可得到待估计的Gold码，组合方法不是本文讨论重点，不再详述，可参考文献[8]。
4 结论
本文在近年来研究热门子空间分解的基础上，提出了一种对带有噪声信号的相关矩阵构造方法。这一方法重新设计了信号相关矩阵的构造算法，利用累乘计算，将各个分段矩阵互乘，计算量与传统构造方法相似。用扩频信号验证了该算法的理论推导与仿真，仿真结果表明，该算法实际计算与理论推导一致，可有效解决低信噪比条件下无法提取扩频用户码序列的问题。同时，该算法也存在缺陷，即该算法需要样本数量足够多，并要保证N和K的取值都较大，这样便可同时在低波动性和高分辨率两项指标上都取得较好的结果。
参考文献
[1] Van Der Veen A, DEPRETTERE E, SWINDLEHURST A. Subspace-based signal analysis using singular value decomposition [J]. Proceedings of IEEE, 1993,81(9): 1277-1308.
[2] Bensley S. E, AAZHANG B. Subspace-based channel estimation for code-division multiple-access communication systems [J]. IEEE Trans.Commun., 2011, 44: 1009-1020.
[3] GUSTAFSSON T, MACINNES C S .A class of subspace tracking algorithms based on approximation of the noise-subspace [J].Signal Processing Transactions on Acoustics, Speech, and Signal Processing IEEE 2010,48(11): 3231-3235.
[4] TUFTS D W, MELISSINOS C D. Simple effective computation of principle eignevectors and their eigenvalues and application to high resolution estimation of frequencies [J]. IEEE Trans. Acoust. Speech.Signal Processing, 2006, 34:1046-1053.
[5] PILLAI S U, BYUNG H K.GEESE (GEneralized Eigenvalues Utilizing Signal Subspace Eignevectors) - a new technique for direction finding [C]. Signals, Systems and Computers, 1988:568-572.
[6] BARUA S, HASHIMOTO T. Suboptimal MMSE multiuser receiver design for DS-CDMA multirate system using spectral correlations [C]. IEEE International Symposium on Information Theory, 2003: 446.
[7] OPPENHEIM A V, SCHAFER R W. From frequency to quefrency: a history of the cepstrum [J]. IEEE Signal Processing Magazine, 2014,21(5):95-106.
[8] NZOZA C N, GAUTIER R, BUREL G. Blind synchronization and sequences identification in CDMA transmissions [J]. IEEE MILCOM, 2004, 3:1384-1390.