文献标识码： A
DOI：10.16157/j.issn.0258-7998.2015.07.025
中文引用格式： 章新城，林灯生，李少谦. 高阶调制下极化码的构造研究[J].电子技术应用，2015，41(7)：88-91，95.
英文引用格式： Zhang Xincheng，Lin Dengsheng，Li Shaoqian. Research on channel polarization of polar codes with high-order modulation[J].Application of Electronic Technique，2015，41(7)：88-91，95.
0 引言
Arikan提出的极化码[1]是一种可以理论证明在任意二进制输入离散无记忆信道下容量可达的码。该码自被发明以来一直引起广泛关注和研究，相关的成果也不断涌现，这些研究集中在极化码的容量限[2-4]、极化码构造[5]以及译码[6-7]等方面。
极化码是一类信道特定码，即不同的信道参数具有不同的极化码，因此如何构造极化码对于所使用的极化码来说至关重要。通常情况下，除了二进制删除信道 (Binary Erasure Channel，BEC)，精确的极化码构造具有很高的复杂度。Arikan在文献[1]提出基于蒙特卡洛仿真的方法实现极化码的构造，而文献[5]提出一种基于密度进化[8]的极化方法，该方法无论在复杂度还是性能方面相比蒙特卡洛的方法都具有一定的优势。
然而，目前有关基于密度进化的方法还只能在二进制输入离散无记忆信道中进行，对于多进制，特别是基于高阶调制的信道并没有特别好的方法。这是由于在高阶调制中，每个符号对应的比特出错概率不相同[9]，而且出错概率会随着发送符号的不同而改变。因此，如果要将极化码直接使用高阶调制进行传输，则极化码的构造过程也随着码字变化而变化。为了解决这个问题，本文提出一种基于平行信道的方法，将高阶调制极化码的构造问题化简为一般的二进制输入信道的极化码的构造问题，巧妙地避免了对高阶调制符号直接进行极化码构造带来的困难。当然，本文方法与文献[10-11]中提出平行信道概念有本质的不同，文献[10]提出利用极化码在平行信道间进行编码以实现发射机在未知信道状态信息情况下达到平行信道容量的目的，文献[11]则研究在发射端已知不同信道的状态信息情况下如何实现平行信道传输，而本文中提出的方法利用传统的平行信道理论无法解决。
本文针对两类最常见的高阶调制：相移键控(Phase-Shift Keying，PSK)和正交幅度调制(Quadrature Amplitude Modulation，QAM)开展研究。对于PSK重点研究最常用的8-PSK，而QAM调制可以分解成两个正交的脉冲幅度调制 (Pulse Amplitude Modulation，PAM)[12]，所以主要以PAM作为研究对象，PAM调制结果可以自然延伸到QAM调制。另外，格雷映射是调制中最常用的映射方式，因此本文中位到符号的映射全部采用了格雷映射。
1 高阶调制下的极化码构造
1.1 8-PSK调制
图1给出了基于一种格雷映射的8-PSK星座图。图1中所有星座点都均匀地分布在一个单位圆上，定义8-PSK的每个星座点对应的比特序列为b3b2b1。假定本文中的高阶调制都经过一个均值为0、方差为N0的AWGN信道。下面将分析星座点对应比特序列的出错概率。
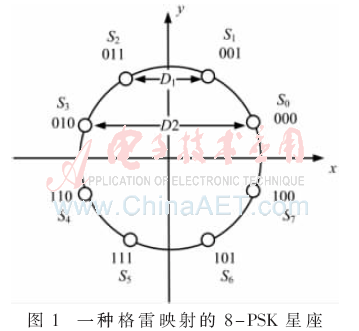
对于高阶调制，当信道信噪比较高时，PSK的某个比特出错概率主要由该比特的取值相反且最近的星座点之间的欧氏距离dmin决定[12-13]，且该比特的出错概率可以表示为：
其中，Q(x)为Q函数[12]，Eb/N0表示单位比特的信噪比。对于b1 bit，由于采用格雷映射，因此，总是可以从相邻星座点中找到与发送b1相反的星座点，因此，无论b1为何值，最小欧式距离都是图中的D1。对于b2 bit，则要分两种情况，一种是当b1=0时，从图1中可以看出，其出错的最小欧式距离为D2，如发送星座点为000，其最易出错星座点为010，即最小欧式距离为D2(因为已知b1=0，所以不可能错成011)；另一种是当b1=1时，从图中可以看出，其出错的最小欧式距离为D1，如发送星座点为001，其最易出错星座点为011，即最小欧式距离为D1。同理，对于b3 bit，它与b2情况恰好相反，即b1=0时，最小出错概率为D1，而b1=1时，最小欧式距离为D2。其中D1=2sin(π/8)，D2=2sin(3π/8)，并根据文献[12]得出D1和D2所对应的二进制输入的AWGN信道的等效噪声方差分别为：
1.2 M-PAM调制
对于M-PAM调制，也可以像8-PSK调制一样等效成多个噪声固定的平行信道。假设基于一种格雷映射的M-PAM的星座点集合为{Si}，其中i=0，1，2，…，M-1，M=2m。假定M-PAM的星座点按照下标从小到大顺序排列，每个星座点与相邻星座点欧氏距离相等，均为2d，星座点对应的比特序列表示为bmbm-1…b2 b1，则该星座图有如下规则：
(1)M-PAM可以与8-PSK一样划分出若干不同的二进制输入的AWGN信道，且等效信道有M/2种。将这M/2种等效信道按照对应的M/2种欧氏距离从小到大的顺序排列，并将排序后的第k个等效信道对应的欧氏距离记为Dk，k=1，2，…，M/2，则Dk可以表示为：
(2)对应任意一个比特序列中的bj，j=1,2，…，m，将会经过第1到2j-1个等效信道中的一种。
(3)假设bj选择的是第l个等效信道，则当bj=0时，选择第(2j-1+l)个等效信道作为bj+1的信道，而当bj=1时，则选择第(2j-1-l+1)个等效信道作为bj+1的信道。
依据上述规律，可以将M-QAM调制等效成多个具有固定信噪比的二进制输入AWGN信道，整个过程以递归的方式进行。首先根据规则(2)先确定b1的信道，由于该情况下只有一种信道k=1，相应噪声方差为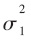
；接着确定b2 bit的信道，根据规则(3)及b1的取值不同，b2有两条可选的信道：当b1=0时候，选择第2个信道，当b1=1时，选择第1信道；以此类推。
M-PAM方案的发射端与接收端处理过程基本与8-PSK方案保持一致，但需要注意两点：(1)与8-PSK情况一样，低比特除了承载信息之外，还要为高比特提供选择信道的信息，因此，接收端对于接收可靠性要求很高，本方案中是采用译码纠错后的低比特信息作为高比特选择信道的信息，这就要求一个调制符号中的每一个比特都要单独编码，因此，需要的编码器的总数为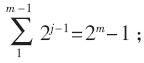
(2)假定调制符号个数为N，根据前一点结论，则一个符号内第j bit需要编译码器个数确定为2j-1个，但该N bit码元具体分配到哪个信道传输则由低比特随机确定的，这会造成每个编码器的码长不一致。为了解决这个问题，提出一种基于比特翻转的方法来克服码长不一致造成的影响。
该方法的基本思想是保持每个比特对应的各个编码器的码长不变，如：对应bj bit，该bit对应的2j-1个编码器的码长都为N/(2j-1)，这样带来后果是有可能出现部分编码器输出的码元不能在按照上述规则计算出的噪声方差的信道上传输。该情况分为两种，一种是本来应该在高噪声方差信道上传输的码元被放在低噪声方差信道上传输，另一种则相反，应在低噪声方差传输的码元被放在高噪声方差信道上传输。总体上，前一种情况会使该码性能恶化严重，后一种情况会使该码性能略微变好。为此，进一步采取方法，通过控制码元出现概率，让两种情况中前一种情况不出现或尽量低概率出现。对于4-PAM调制，如果b1中“0”的个数比“1”多，则b2就会出现后一种情况，否则，就会出现前一种情况。另一方面，由于极化编码时最后一个信息比特参与了所有码元生成的过程，改变该比特的值，就相当于对整个码字实现了一次比特翻转，因此可以通过控制信息比特最后一个比特值(该比特将不再用来传输信息)来调节b1中“1”和“0”个数，使得b2只出现后一种情况。
2 仿真结果分析
首先分析8-PSK调制时极化码的性能。如图3所示，极化码的码长分为N=256和N=512两种情况，根据公式(2)计算出两种等效噪声方差，分别为6.828 4 N0和1.171 6 N0，其中N0根据仿真需要来设定，并选择b1、b2和b3码率为0.51、0.51、0.98，平均吞吐量为2 bit/符号，然后依据这些参数利用文献[5]的方法进行极化码的构造。
由图3可以看出，与同样吞吐量为2 bit/符号的正交相移键控(QPSK)比，两个码在误码率都保持在10-4时，分别有1.9 dB和2.4 dB的性能增益。另外，也给出了两种码长下接收端理想已知C1(传输b1的极化码记作C1)和依靠译码器接收结果的C1两种情况的性能对比，从图3可以看出，非理想情况与理想情况的性能差异都在0.3 dB以内，性能恶化不是很严重。
图4给出了采用16-QAM调制时候(两路4-PAM)极化码的误码率性能，对于每个4-PAM调制，极化码的码长分为N=256和N=512两种情况，根据式(3)、式(4)可以算出其两种等效噪声方差为N0和0.111 1 N0，其中d=1。选择b1码率为0.42，b2是由两个码长为N/2的极化码组成，码率分别为0.38和0.78，此时一个4-PAM的平均吞吐量为1 bit/符号。
由图4可以看出，与同样吞吐量为2 bit/符号的QPSK相比，在误码率为2×10-5时，其增益分别有1.3 dB和1.8 dB。同样，在图4中，也给出了两种码长下接收端理想已知C1和依靠译码器接收结果的C1两种情况的性能对比，并且，性能恶化也不是很严重。
3 结论
本文先是分析了格雷映射下PSK调制和PAM/QAM调制星座图的特点，并根据各自特点，得出了可以将高阶调制信道分解成多个平行的并具有固定噪声功率的二进制输入子信道的结论，并利用此结论，将高阶调制极化码的构造问题转化为一般的二进制输入信道的极化码的构造问题，从而避免了传统方法在高阶调制时候无法确定信道噪声功率的问题，实现了高阶调制时的极化码的构造。本文最后还针对PSK调制和QAM调制在采用推荐方法后的性能进行了仿真，仿真结果也表明了采用推荐方法可以带来较为显著的性能提升。
参考文献
[1] ARIKAN E.Channel polarization: a method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J].IEEE Trans.Inf.Theory，2009，55(7)：3051-3073.
[2] ARIKAN E，TELATAR E.On the rate of channel polarization[C].IEEE Int. Symposium on Inf.Theory，Seoul，Korea，2009：1493-1495.
[3] KORADA S B，SASOGLU E，URBANKE R.Polar codes：characterization of exponent，bounds，and constructions[C].Proc.2009 IEEE Int.Symposium on Inf.Theory，Seoul，Korea，2009：1483-1487.
[4] HASSANI S H，KORADA S B，URBANKE R.The compound capacity of polar codes[C].47th Annual Allerton Conference，Illinois，U.S.A.，2009：16-31.
[5] MORI R，TANAKA T.Performance and construction of polar codes on symmetric binary-input memoryless channels[C].IEEE Int.Symposium on Inf.Theory，Seoul，Korea，2009：1496-1500.
[6] TAL I，VARDY A.List decoding of polar codes[C].Proc.IEEE Int.Symposium on Inf.Theory，St.Petersburg，Russia，2011：1-5.
[7] Niu Kai，Chen Kai.Stack decoding of polar codes[J].Electronics Letters，2012，48(12)：695-697.
[8] RICHARDSON T，URBANKE R.Modern coding theory[M].U.K.：Cambridge University Press，2008.
[9] MASNICK B，WOLF J.On linear unequal error protection codes[J].IEEE Trans.Inf.Theory，1967，4(3)：600-607.
[10] HOF E，SASON I，SHAMAI S，et al.Capacity-achieving polar codes for arbitrarily permuted parallel channels[J].IEEE Trans.Inf.Theory，2013，59(3)：1505-1516.
[11] Chen Kai，Niu Kai，Lin Jiaru.Practical polar code construction over parallel channels[J].IET Communications，2013，7(7)：620-627.
[12] GOLDSMITH A.无线通信[M].北京：人民邮电出版社，2007.
[13] Lin Dengsheng，Xiao Yue，Li Shaoqian.Low complexity soft decision technique for gray mapping modulation[J].Wireless Personal Communications，2008，52(2)：383-392.