0 引言

    随着云计算的广泛应用，云端的存储、网络带宽、GPU、处理器等资源日益紧缺^[1]。部分应用程序非法或过多地占用某些云端资源，导致其他应用程序或服务运行效率下降，甚至导致服务器端崩溃等严重后果，为防止此类情况发生，需对云端资源进行有效监控^[2]。

    云端的大数据与分布式平台为资源监控带来了极大的困难，若对云端大数据采集样本并分析，此过程的计算成本极高，另一方面，若为了降低计算成本而增加采样周期，则会导致监控过程不够完整，导致部分重要的棘波丢失^[3-5]。

    针对以上问题，本文提出一种自适应云端资源监控算法，包括训练和监控两个阶段。训练阶段，采集适量的数据样本训练，估算出最佳的监控参数组合；监控阶段根据受监控资源的变化剧烈程度自适应地调节采用周期，以此保证监控算法的计算效率与监控质量达到较好的平衡。

1 问题定义

    对于云端大数据下的资源监控，最为有效的方案是，在不损失其统计性能的前提下，尽可能地降低监控的目标数据的量，显然，需为此寻找一个合适的阈值。首先定义两个与资源监控质量相关的重要参数G和Q。

    第一个参数G如下定义：

式中，N(t)表示监控算法采集的样本数量，N(t⁰)表示理论采样频率采样的样本数量，t⁰表示最高的理论周期(即1 s)。G值的范围为[0，1]，G值越高表示采样周期越短，而计算与带宽开销越高。

    第二个参数Q(质量)代表了监控算法是否能准确反映系统资源的变化情况。Q的质量必须综合考虑两个因素：(1)采样周期过大导致的监控不完整，(2)对资源变化的棘波监控能力。因此将Q定义为两个重要统计参数的组合：NRMSE为归一化均方根误差，Fmeasure为棘波检测的精度与召回率的带权均值。

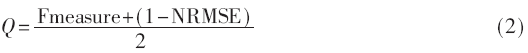
式中，Fmeasure与NRMSE的取值范围均为[0，1]，Q的取值范围为[0，1]。综合Fmeasure与NRMSE对资源评价的原因在于：云端资源变化极为剧烈，无法仅通过NRMES对其变化作出准确的反应，而Fmeasure可对棘波资源的检测效果较好，因此综合两个参数来提高资源评价的准确性。Fmeasure计算方式如下：

式中，precision表示精度，recall表示召回率，Fmeasure值越接近1代表检测的质量越高。

    将监控算法的阈值表示为G与Q的加权之和：

式中ω∈(0，1)是一个调谐常量，由服务器端管理员设定。ω>0.5，则G的重要性高于Q；反之，G的重要性低于Q；ω=0.5，两者重要性相等。

    已有的监控算法以固定的采样周期采集样本，仅当新数据与历史数据有所差异时，才将新数据保存并转发至分析模块。尽管该方案可获得较高的G值，但其导致了较高的检测错误以及较低的Q值(丢失了较多的棘波)。图1所示为两个场景举例，图1(a)的采样周期为1 s(低G与高Q)，图1(b)的采样周期较长，采样数据数量较少，同时也丢失了大量的棘波数据。

2 自适应云端资源监控

    自适应云端监控由训练阶段与自适应监控阶段组成，训练阶段估算最优参数组合，自适应监控阶段是监控系统的核心部分。

2.1 参数定义

    监控算法分析采样的数据，当资源相对稳定时，降低监控数据的数量，在资源变化剧烈时，增加监控数据的采样数量。以此，降低计算与带宽开销，同时保证不错过重要的系统棘波变化。本算法动态地设置两个关键变量：采样周期t与变化性Δ。采样周期t越短，收集的数据量越大，设t_m表示采样周期的最小值，t_M表示采样周期最高值，显然t_M≥t_m。Δ代表了连续采样样本的偏差，若Δ较低，认为监控资源比较稳定。本文考虑两个Δ相关的参数：

    (1)峰值变化性Δ_p：表示连续样本间偏差的阈值，当Δ>Δ_p时，表示棘波。

    (2)容错变化性Δ_q：表示连续样本间偏差，Δ_q≥Δ_p表示高变化性。当监控数据的变化性过高时，需将采样周期设为t_m，从而抓取资源变化的细节特点。将t与Δ相关阈值的最优值设为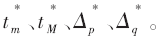

2.2 训练阶段

    训练阶段求解最优阈值参数训练阶段通过最大化式(4)的E，将训练数据样本数设为λ。

    算法1所示为训练的伪代码，初始化阶段将E的最优值E^*设为0，最小采样周期设为t⁰，X_tmp设为周期t⁰采样的监控数据序列。循环迭体中，对监控周期t与变化性Δ进行迭代处理。AdaptiveMonitor为数据监控算法，结果数据存储于X变量中，然后，计算质量参数Q、参数G与阈值E。最终，更新最优阈值参数将结果阈值赋予监控算法的核心阶段。

    算法1：训练阶段1

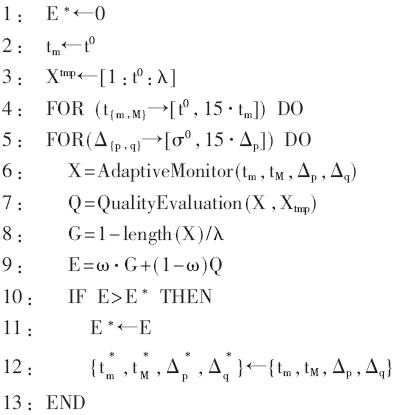
    算法2计算Q参数的值，在初始化阶段，采样数据起始点为确定值，将NRMSE设为0，计算原时间序列X_tmp的变化范围。之后的循环体中，轮流使用各时间点数据来计算参数Q的质量。6~10行提取时间序列x₀与时间i，11行更新采样序列的平方差之和，然后，分别计算NRMSE、精度、召回率，最终计算Fmeasure与Q参数。

    算法2 训练阶段2

2.3 自适应的监控阶段

    算法3所示为自适应监控阶段的伪代码。初始化阶段，将采样周期设为最小值Δ设为0，∈_inc设为10，该变量用于触发最低采样周期(t⁰)，在∈·λ个采样之后，获得了X值。变量k是对采样序列X的计数，若k>λ，则结束X的采样。

    监控算法的主体是一个死循环，首先使用实时采样更新偏差Δ值，若Δ值未变化，则增加采样周期长度，若Δ值变化较大，则减小当前的采样周期。监控过程中，通过计算Q参数与训练阶段的最优参数，实现实时自适应的动态调整，从而实现高准确率的采样与低成本的平衡。

    算法3 实时监控阶段

3 实验测试床与数据集训练

3.1 测试床

    本文试验使用Amazon EC2^[6]监控平台。其中监控节点的PC配置为：AMD处理器2 218 HE，主频2 600 MHz，缓存1 024 kB，每个节点的网络带宽为10 Mb/s，受监控的节点运行一些服务与应用程序，如Apache2、MySQL、Java程序等，数据库使用MySQL数据库。试验对100个节点(包括软件虚拟出的节点)进行监控，监控过程达10个小时。

3.2 训练集大小设置

    训练集大小λ对算法的计算开销影响较大，因此，在保证算法高质量监控的同时，限制其成本极为重要。试验对资源使用自适应监控算法，将λ分别设为5~200进行统计，图2所示为λ对三个重要参数的影响。图中可看出ω=0.25时，Q值最优，ω=0.75时，G值最高。分析其原因：训练集较小时，少量数据之间的差异较大，将被分辨为棘波。而采样周期较小时，可获得较高的Q和较低的G。

    图2(c)中显示，不同训练集大小对E参数的影响。E参数范围为80%~88%。可看出当ω较小时，应使用较小的λ值，ω较大时，使用较高的λ值。综上，若管理员需要平衡的G与Q，则将样本数量选为50~150较为合适。

4 试验结果与分析

4.1 本文自适应算法与静态delta算法的检测性能比较

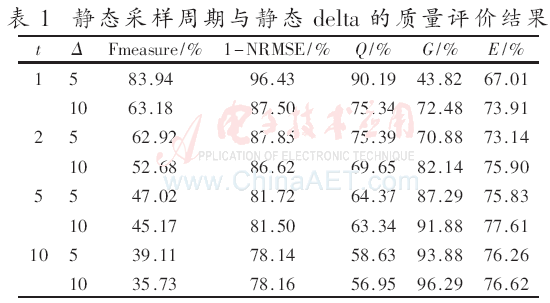
    表1所示为静态采样周期(t)与静态delta(Δ)下获得的试验结果，表2所示为自适应算法获得的结果。结果显示：当λ=5时，E值为76.54%，当λ=100时，E为79.37%。比较表1与表2可看出，自适应算法的平均性能高于静态算法，此外自适应算法的Fmeasure始终高于65%，可见本算法提高了棘波捕获的能力。

4.2 资源消耗比较

    图3所示为本自适应算法与静态算法的资源消耗比较，图3(a)所示为静态采样周期算法与静态阈值算法的CPU使用率随时间的变化情况，图3(b)为本文自适应算法的CPU使用率的变化情况，可看出在整个监控时间之内，本算法的平均CPU占用率明显低于两种静态算法。图3(b)可看出本算法的3个阶段：(1)收集?姿个训练数据集，该阶段CPU使用率呈上升趋势；(2)自适应算法计算最佳参数，此时引起了较高的CPU使用率的棘波；(3)自适应监控阶段，可看出本算法通过自适应的调节，使得整个CPU资源使用率处于平稳状态。

5 结束语

    本文针对分布式云计算的云端资源监控提出了自适应的监控算法，获得了云端监控准确率与计算成本较好的平衡，试验结果也佐证了本算法的有效性。未来将研究多个统计参数的不同效果，进一步提高本算法对资源变化剧烈程度估算的准确性。

参考文献

[1] 陈康，郑纬民.云计算: 系统实例与研究现状[J].Journal of Software，2009，1(20).

[2] 罗军舟，金嘉晖，宋爱波，等.云计算：体系架构与关键技术[J].通信学报，2011，32(7)：3-21.

[3] 华夏渝，郑骏，胡文心.基于云计算环境的蚁群优化计算资源分配算法[J].华东师范大学学报：自然科学版，2010(1)：127.

[4] 冯登国，张敏，张妍，等.云计算安全研究[J].软件学报，2011，22(1).

[5] 刘正伟，文中领，张海涛.云计算和云数据管理技术[J].计算机研究与发展，2012，49(1)：26-31.

[6] ANDREOLINI M，COLAJANNI M，PIETRI M.A scalable architecture for real-time monitoring of large information systems[C].Network Cloud Computing and Applications (NCCA)，2012 Second Symposium on.IEEE，2012：143-150.