摘 要: 目前车模倾角一般采用陀螺仪或加速度计进行测量。然而单纯利用其中一种传感器采集到的信号存在极大误差,无法满足二轮自平衡车直立控制的需要。为此,采用陀螺仪和加速度计测量倾角,并应用卡尔曼滤波算法对上述两种信号进行融合,得出理想的输出倾角。同时,将得到的卡尔曼滤波程序移植到车模直立控制程序中,进行车模直立控制试验。试验结果表明,运用该方法可以得到很好的滤波效果。
关键词: 卡尔曼滤波;平衡车;直立控制;数据融合
二轮直立平衡车模型经简化可等价为一个倒立摆模型,对于其平衡的控制,需要得到车模精确的倾角。通过加速度计和陀螺仪的测量,可以得到车模的加速度和角速度,进而可以换算出车模的倾角和倾角变化率。然而由于车模本身的运动会产生很大的干扰信号,使得加速度计无法准确测量车模的加速度。同时,由于陀螺仪的温漂效应,也无法通过积分得到车模的准确倾角。在此情况下,为得到精确的车模倾角,需要采用多传感器进行信号融合处理[1]。本文利用卡尔曼滤波算法,对加速度和陀螺仪采集到的信号进行数据融合,比较精确地实现了车模倾角的测量。
1 陀螺仪和加速度计测量模型
1.1 陀螺仪测量角速度
陀螺仪可以用来测量物体的旋转角速度。本文所选用的陀螺仪为意法半导体(ST)生产的三轴数字陀螺仪L3G4200D,可提供16位数据输出。当器件旋转时会产生相应的旋转角速度输出信号。在车模上安装陀螺仪,可以测量车模倾角角速度,将角速度进行积分便可以得到车模的倾角。然而,在实际情况下,陀螺仪会发生一定程度的漂变,尤其是温漂,给陀螺仪的测量带来很大的干扰。因此所测得的角速度存在微小的偏差和漂移时,经过积分作用,会产生累积误差。显然,该倾角值也不能当作车模直立控制的控制信号。
1.2 加速度计间接测量倾角
加速度传感器可以用来测量由地球引力作用或者物体运动所产生的加速度。本文所选用的加速度计为飞思卡尔公司生产的MMA8451Q,最高具有14位数据输出精度。利用加速度计其中一个方向上的加速度值,通过计算,便可间接测量车模的倾角信号。本文利用Z轴上的加速度信号,计算得到车模的倾角。图1是利用加速度计Z轴信号来间接测量车模倾角信号的原理图。

当车模发生倾斜时,重力加速度g会在Z轴产生一个加速度分量,使Z轴输出信号改变。输出关系为:

其中,g为重力加速度,θ为车模倾角,k为加速度传感器灵敏度系数[2]。
当倾角θ比较小时,输出信号的变化可以近似与倾角成正比,然而在实际情况下,由于车模本身的摆动会产生很大的干扰,使得加速度计输出信号无法准确反映车模倾角,因此,纯粹通过加速度计也无法得到需要的车模倾角信号。
为了获得相对精确的车模倾角信号,需要对陀螺仪和加速度计的输出信号进行融合,本文采用的是卡尔曼滤波法。
2 卡尔曼滤波原理及滤波器设计
2.1 卡尔曼滤波概述
卡尔曼滤波是一个最优化自回归数据处理算法。它属于一种软件滤波方法,其基本思想是:以最小均方误差为最佳估计准则,采用信号与噪声的状态空间模型,利用前一时刻的估计值和当前时刻的观测值来更新对状态变量的估计,求出当前时刻的估计值,算法根据建立的系统方程和观测方程对需要处理的信号做出满足最小均方误差的估计[3]。
2.2 卡尔曼滤波器设计
2.2.1 时间更新
在卡尔曼滤波器中,时间更新的过程是一个预测过程。时间更新算法是关于卡尔曼滤波器中预测器的描述。预测器的任务是依据上一时刻的数据预测当前时刻的数据,具体可分为状态估计和方差估计[4-6]。
2.2.2 测量更新
测量更新的过程本质上是一个校正过程。校正器的任务是将先验状态估计值与当前的倾角数据相融合,改善先验状态估计值,从而得到当前时刻的后验状态估计值。具体可分为以下几步:加速度计的测量参差计算,残差的协方差计算,最优卡尔曼增益计算,校正先验状态估计值和计算后验状态估计值,校正先验估计协方差矩阵,计算后验估计协方差矩阵[4-6]。
3 卡尔曼滤波器在车模中试验
小车加入了SD卡模块,可以记录小车运行状态,并用MATLAB分析设计,这样大大方便了设计解算小车姿态角度的卡尔曼滤波器。用手晃动车子,使车子的姿态角度不断发生变化,用SD卡记录数据,用MATLAB分析数据。
简单用加速度计输出得到的角度信号如图2所示。

由图2可以看出,信号噪声很大,动态性能很差,但是静态性能较好,如图中箭头所示,角度相对稳定不变时,能正确反映车子的姿态角。
简单用陀螺仪的角速度积分输出的角度信号如图3所示。

用单纯的角速度积分得到的角度信号十分平滑,动态性能非常好,但是随着积分进行,静态误差越来越大。由图3可以看出曲线有整体向下移动的趋势,这是静态误差积累的结果。
把加速度信号和陀螺仪信号送入卡尔曼滤波器之后输出的角度信号如图4所示。

x=[angle(1);drift(1)];
for i = Time(2:end)
x = A*x+B*u_gyro(i);
P = A*P*(A')+Q;
y = z_inc(i)-x(1);
s = P(1,1)-R;
K = P*[1;0]/s;
x = x + K*y;
P = ([1,0;0,1]-K*[1,0])*P;
angle(i) = x(1);
drift(i) = x(2);
end
由图4可以看出,滤波器输出的角度十分平滑,动态性能较好,且消除了静态误差。
综合对比滤波前后的角度信号,如图5所示。

4 卡尔曼滤波器参数设置
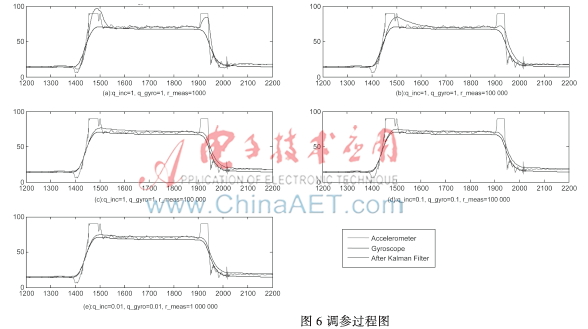
调参过程可按下面步骤进行,效果如图6所示。
(1)随便设置参数为
q_inc=1;
q_gyro=1;
r_meas=1 000;
效果如图6 (a)所示。可以看出,系统响应角度跟踪时受加速度计噪声影响很大,在角度剧烈变化时有严重超调,且在稳态时,角度有波动,滤波器未能很好地抑制加速度计的高频噪声。造成这种现象的原因是加速度计的噪声很大,而设置的r_meas测量方差比实际的小,导致滤波器没能很好地滤除噪声,这时可以选择增大r_meas。
(2)调整参数为:
q_inc=1;
q_gyro=1;
r_meas=100 000;
效果如图6 (b)所示,稳态的时候曲线变得十分平滑,可见滤波器很好地抑制了加记高频噪声的干扰。角度跟踪超调减小,但是仍然严重,试着继续增大r_meas。
(3)再次调整参数为:
q_inc=1;
q_gyro=1;
r_meas=10 000 000;
效果如图6 (c)所示,发现继续增大r_meas效果改善不再明显,而且角度收敛变得特别缓慢,动态性能降低。造成这种现象的原因是r_meas设置过大,导致系统把加记有用信号也当成了噪声。陀螺仪的噪声是很低的,陀螺仪零漂的噪声也是很低的,考虑到这个,可以选择减小Q,并把r_meas恢复到前面的值。
(4)减小Q:
q_inc=0.1;
q_gyro=0.1;
r_meas=100 000;
效果如图6 (d)所示,系统动态响应明显改良,角度输出能很好跟踪,且不出现大幅度超调。
(5)继续减小Q:
q_inc=0.01;
q_gyro=0.01;
r_meas=100 000;
效果如图6 (e)所示,输出性能有小幅改善,达到满意效果。再继续减小效果不大,因此,可把这一组参数作为最终参数。
5 卡尔曼滤波器移植到车模控制器中
把参数下载到车模控制器中,查看车模直立控制效果,记录下运行数据,评估卡尔曼滤波器效果。某一段时间内系统滤波前后对比如图7所示,由此可见滤波器效果十分理想,滤波器设计圆满完成。
本文研究了基于卡尔曼滤波的陀螺仪和加速度计的数据融合方法,利用陀螺仪和加速度计测量车模的角速度和加速度,将采集到的数据导入matlab中,应用卡尔曼滤波算法对其进行数据融合,不断整定参数,使得输出倾角达到理想效果。同时,将得到的卡尔曼滤波程序移植到车模直立控制程序中,进行车模直立控制试验,试验结果表明,运用该方法可以得到很好的滤波效果。
参考文献
[1] 冯智勇,曾瀚,张力,等.基于陀螺仪及加速度计信号融合的姿态角度测量[J].西南师范大学学报(自然科学版),2011,36(4):137-141.
[2] 竞赛秘书处.第七届全国大学生“飞思卡尔”杯智能汽车竞赛电磁组直立行车参考设计方案(版本1.0)[EB/OL]. [2011-12-22](2014-07-a)http://www.smartcar.au.tsinghua.edu.cn/upload_files/atta/1383549696785_37.pdf.
[3] 彭丁聪.卡尔曼滤波的基本原理及应用[J].软件导刊,2009,8(11):32-34.
[4] 阮晓钢,蔡建慕,李欣源,等.两轮平衡机器人的研究与设计[M].北京科学出版社,2012.
[5] KALMAN R E.A new approach to linear filtering and prediction problems[C].Transaction of the ASME-Journal of Basic Engineering,1960,82(D):35-45.
[6] 高嵩,潘泉,肖秦琨,等.多传感器自适应滤波融合算法[J].电子与信息学报,2008,30(8)::1901-1904.

