摘 要： 数字水印技术是一门将数字信息嵌入多媒体数据并能提取的一门技术。本文提出一种基于双正交小波变换和图像复杂度的可逆水印算法。该算法对原始图像进行双正交离散小波变换后分解成频带，基于熵的值决定嵌入频带，通过图像复杂度的五个特征值决定嵌入位置。仿真结果表明，该算法取得良好的效果，且能较好地抵抗模糊、噪声、锐化等滤波操作，具有良好的鲁棒性。
关键词： 双正交小波变换；熵；图像复杂度；鲁棒性；PSNR；NC
0 引言
如今，随着互联网时代的到来，数字媒体产业飞速发展。人们生活得到极大便利，同时也使版权侵犯、信息篡改等行为变得更加容易和简单。因此版权保护问题成为网络安全中的突出问题。而数字水印技术就是为信息隐藏和数据安全提供高质量的解决方案的一门技术[1]，在计算机科学、密码技术、信号处理、图像处理等领域有着广泛应用前景。
近年来，针对数字水印的研究已经取得了很大进展，特别是基于频域上的数字水印成为研究热点。然而，现有大多数文献中图像水印嵌入方案都是在低频子带将水印嵌入整个原始图像, 并未考虑原始图像自身复杂度特征。基于以上问题，本文提出一种基于双正交小波变换和图像复杂度的可逆数字水印算法。其主要特点如下：
（1）最佳频带的选择：选取双正交小波基进行二维离散小波变换，对高频小波系数计算熵值，选取最大熵值所在频带作为最佳嵌入频带。
（2）最佳位置的选择：将图片进行分块，对每个图片块计算它的图像复杂度值，选取最优值所在图片块作为嵌入位置。
（3）实现可逆水印，而且水印提取不需要原始水印的参与，实现盲可逆水印。
1 相关知识
1.1 双正交小波变换
目前数字水印算法中通常采用正交小波基，与正交小波基相比，双正交小波是一种紧密联系的、具有精确的重构信号平衡性的对称小波，非常适用于数字水印信息嵌入；双正交小波同时拥有正交性和对称性，在图像处理领域优势更加明显。本文算法中选用 Daubechies9/ 7 双正交小波, 它是最适合用于数字水印的双正交小波基之一[2]。
1.2 图像复杂度
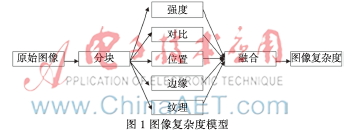
HVS、Osberger等人[3-4]提出了图像复杂度模型，此模型由强度、对比、位置、边缘、纹理5个参数组成，如图1所示。此方法将图像分为若干块，对每个块分别计算五个参数值，以此估算图像块的图像复杂度。
2 水印嵌入算法
本文提出一种基于双正交小波变换和图像复杂度的盲可逆水印算法。在水印嵌入算法中，关键在于最佳频带以及最佳嵌入位置的选择。
2.1 最佳嵌入频带选取
具体步骤如下：
（1）双正交离散小波变换
基于双正交小波基，对原始载体图像G进行二级离散小波变换，得到4种子带，分别是LLn，LHn，HLn和HHn[2]。
（2）计算高频小波系数熵
熵是随机变量的不确定性度量方法。计算熵值的公式如下[5]：
在本文算法中，对高频小波系数（CHn，CVn和CDn）利用公式（1）计算信息熵，熵值分别为Ech，Ecv，Ecd。
（3）选择最佳嵌入频带
选取最大的熵值EX所在的频带X为最佳频带。公式如下：
2.2 最佳嵌入位置选择
利用图像复杂度模型[3-4]综合确定最佳嵌入位置。
（1）原始载体图像分块
假设原始载体图像G大小为m×n，整个图像被分成y块，且每块Bi(0＜i＜y)的尺寸为p×q，即m×n=y×p×q。
（2）计算图像块的复杂度值
①强度（Intensity）
强度参数指的是图像中的像素点的亮度。基于人类视觉模型（HVS），人眼对于图像中心区域的强度畸变最敏感。因此，计算公式为：
式中，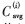
为Bi块的平均强度，![@4_8_5`]HQUJ~F~ACS($P3A.jpg](http://files.chinaaet.com/images/2015/09/15/6357794026566600001706952.jpg "@4_8_5`]HQUJ~F~ACS($P3A.jpg")
为图像G的平均强度。
②对比（Contrast）
对比度特征取决于人眼分辨亮度差异的能力。基于人类视觉模型（HVS），图像块的亮度相对于相邻图像块的亮度差异越大，对比特征越明显。因此，计算公式为：
式中，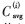
为Bi块的平均亮度， ![@4_8_5`]HQUJ~F~ACS($P3A.jpg](http://files.chinaaet.com/images/2015/09/15/6357794030337800002125195.jpg "@4_8_5`]HQUJ~F~ACS($P3A.jpg")
为相邻块的平均亮度。
③位置（Location）
位置特征指的是图像的中心位置的感知比其他位置更重要。因此，计算公式为：
式中，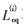
为子图像中心区像素总数，![`YIUAF@TYRV%)1({GCO_][1.jpg](http://files.chinaaet.com/images/2015/09/15/6357794018986300004226539.jpg "`YIUAF@TYRV%)1({GCO_][1.jpg")
为图像块中像素总数。
④边缘（Edginess）
边缘特征指的是提取图像中不连续部分的特征。基于人类视觉模型（HVS），水印的嵌入应该避免影响到图像边缘区域。
本文算法采用Canny边缘检测算法计算边缘特征。算法的阈值取值为0.7[5]。
⑤纹理（Texture）
纹理特征指的是图像的某种局部性质。基于人类视觉模型（HVS），人眼对纹理区噪声较不敏感。因此，通过计算每个图像块的像素值的方差来表示，高方差值表示子图像不是平滑的。计算公式为：
式中，var为方差算子，T(i)为图像块中的像素的灰度值。
（3）归一化处理参数值
将5种参数的重要性测度值进行归一化处理，计算公式为：
式中，Z为参数的图像复杂度值；A为参数图像复杂度最大值。
归一化后，所有的值都在[0,1]区间内，相对应的Bi块的重要性的参数值表示为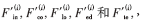
，图像块的组合重要性测度值计算公式为：
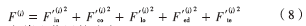
（4）嵌入位置的选取
这里，将嵌入频带子图像分成16块，计算每一个图像块的F(i)，选取F(i)中最大的四个图像块作为嵌入位置。
2.3 数字水印嵌入算法
假设原始载体图像为G，像素值为Si，数字水印嵌入算法步骤如下：
⑴预调整大小：将原始载体图像G调整为灰度图像，且大小调整为（M×N）；
⑵选取最佳频带：具体步骤见2.1节；
⑶选取最佳位置：具体步骤见2.2节；
⑷嵌入数字水印：
①选取二值图像Wk作为水印图像；
②选取与最佳嵌入频带（X）相关的随机数r；
③嵌入数字水印过程：当水印图像像素为0时，将水印嵌入到原始载体图像中，当水印图像像素为1时，不嵌入数字水印。计算公式为：
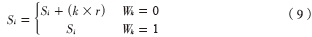
⑸得到嵌入水印的图像G'。
3 数字水印提取算法
数字水印提取算法步骤如下：
⑴对嵌入水印图像G'进行基于双正交小波基的2阶IDWT逆变换；
⑵基于熵，选择最大熵所在频带；
⑶基于图像重要性测度值，选择最大值所在位置Vi；
⑷提取数字水印：
①选取Vi作为提取水印位置；
②选取相关的随机数r ；
③提取数字水印过程：当随机值的一半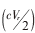
大于平均值(ui)时，提取的水印图像像素为0，否则水印图像像素为1：
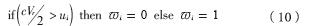
⑸得到水印图像w。
4 仿真结果分析
4.1 实验性能分析
为了验证本文数字水印算法的有效性，以Matlab为实验平台进行仿真。采用Cameraman灰度图像和Lena彩色图像作为原始载体图像，水印图像为“江海学院”二值图像。采用PSNR和NC作为评价指标[6]。
Cameraman灰度图像和Lena彩色图像实验数据如图2和图3所示。在无攻击情况下，由公式计算得出PSNR值分别为30.376 dB、30.006 dB，表明水印嵌入后不可见性较好；计算得出NC值都为1，表明提的水印图像与原始水印图像相似度非常高。
4.2 鲁棒性分析
通过滤波技术对Cameraman和Lena嵌入水印后的图像进行鲁棒性分析。分别采用反锐化滤波器、模糊滤波器和噪声滤波器进行实验，具体结果如表1和表2所示。从表中得知，本文提出算法在使用各种滤波器后还能提取出水印，实现了较好的鲁棒性。
4.3 比较分析
参考文献[8]提出一种可选的预测误差直方图修改的可逆水印算法。将该算法与本文算法的鲁棒性实验结果及平均NC值进行对比，如表3和表4所示。由表可知，本文提出的算法具有一定的优势。
5 结论
本文算法是基于双正交小波变换和图像复杂度模型
提出的。首先对原始载体图像进行双正交小波变换，然后基于最大熵选取嵌入频带、基于图像复杂度模型选取嵌入位置，根据嵌入位置嵌入二值水印图像完成水印的嵌入。水印提取过程不仅可以提取水印图像，还可以还原原始图像，且提取过程不需要原始图像的参与，实现盲可逆水印。仿真实验结果表明该算法取得良好的效果，是一种鲁棒性较强，性能较好的算法。
参考文献
[1] 杨秀清，马红卫，顾新，等. 信息隐藏技术的应用展望[J].信息安全与通信保密，2006,21(8):16－18.
[2] 刘九芬，黄达人，胡军全. 数字水印中的双正交小波基[J].中山大学学报( 自然科学版)，2002,41(4) : 1-5.
[3] Osberger W, Maeder A J.Automatic identification ofperceptually important regions in an image[C].IIth International Conference on Pattern Recognition, 1998:701-704.
[4] Yaghmaee F, Jamzad M. Estimating watermarking capacity in gray scale images based on image complexity[J]. EURASIP Journal on Advances in Signal Processing, 2010(4):1-9.
[5] 彭玉华. 小波变换与工程应用 [M].北京:科学出版社, 1999.
[6] Yaghmaee F, Jarnzad M. Introducing a new method for estimationImage complexity according to calculate watermark capacity[C]. Intelligent Information Hiding and Multimedia Signal Processing,2008:981-984.
[7] 陈艳丽，杨高波. 基于感兴趣区域的彩色图像数字水印[J].计算机与数字工程，2010,36(8):168-171.
[8] Ou Bo, Zhao Yao, Ni Rongrong.Reversible watermarking using optionalprediction error histogram modification[J]. Neuro computing, 2010,93(9):67-76.