摘 要: 针对核脉冲全谱数据采集技术中采用的深度加权滤波法在数据量少时平滑效果差、滞后大的缺点,设计了卡尔曼滤波算法替代传统滤波算法进行解谱的方案。滤波算法首先根据信号与噪声的状态空间模型,建立状态方程和测量方程,然后根据广义卡尔曼滤波对测量方程进行更新,最后根据现场的标准刻度井测量数据确定测量矩阵,对测量数据进行滤波。实测结果表明,该滤波算法相对于传统滤波算法,能够消除谱图的统计涨落,提高光滑度,遏制滞后,并保证滤波后曲线不失真。
关键词:卡尔曼滤波;数据处理;核脉冲全谱数据采集系统;解谱
0 引 言
核脉冲全谱数据采集技术是新一代放射性测井仪器的核心技术。由系统的放射源发出662 kev γ射线,在地层中经过一次或多次的康普顿散射和光电效应,经物理探测窗口进入NaI晶体,产生与入射能量成正比例的光电信号。 光电信号经光电倍增管形成核电子脉冲信号。核脉冲信号A/D转换,分道测量计数[1],上传地面计算机,形成全谱数据谱线。由于计数器存在严重的统计涨落,必须去伪存真,以便资料分析。
其信息处理技术的关键是实测谱的解析技术。解谱方法采用深度加权滤波法。公式如下:
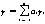 (1)
(1)
其中,y是n个采样值的加权平均值,yi是加权因子,ai是加权系数,各个加权系数均为小于1的小数,且满足总和等于1的约束条件。计算虽然简单,但是需确定归一化因子的值,即需要确定ai的值,且在数据量少时平滑效果差、滞后大。
本文设计的卡尔曼滤波能够消除谱图的统计涨落,提高光滑度,遏制滞后,实现测井数据的有效滤波。
1 卡尔曼滤波的模型建立
1.1 建立系统的状态方程
卡尔曼滤波以最小均方误差为估计的最佳准则,以此来寻求一套递推估计的算法,其基本思想是:采用信号与噪声的状态空间模型,利用前一时刻的估计值和现时刻的观测值来更新对状态变量的估计,求出现时刻的估计值。它适合实时处理和计算机运算[2]。
卡尔曼滤波注重对象的物理过程描述,要求先建立系统的状态方程,由于地层的变化是未知的,很难用一组确定的微分方程加以描述,因此采用一阶高斯马尔科夫过程描述地层变化。
首先设核脉冲个数α和每道脉冲能量β为状态变量(X1,X2)[3],有:
 (2)
(2)
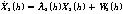 (3)
(3)
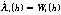 (4)
(4)
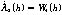 (5)
(5)
式(2)~式(5)中,h表示井的深度,λ1(h)、λ2(h)是非奇异状态转移矩阵,是随井深变化的斜率参数。W1(h)~W4(h)是动态噪声,方差为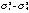 ,均值为零。
,均值为零。
参数λ1(h),λ2(h)是局部随机变化的。若测井井段类似于均匀的地层区,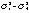 f取得足够小时,λ1(h)、λ2(h)趋于零,则有
f取得足够小时,λ1(h)、λ2(h)趋于零,则有 当测井井段跨越一个地层界面时,λ1(h)、λ2(h)根据X1(h)、X2(h)的变化斜率取正值或负值。若把λ1(h)、λ2(h)设为增广状态变量X3(h)、X4(h),则状态方程可表示为:
当测井井段跨越一个地层界面时,λ1(h)、λ2(h)根据X1(h)、X2(h)的变化斜率取正值或负值。若把λ1(h)、λ2(h)设为增广状态变量X3(h)、X4(h),则状态方程可表示为:
 (6)
(6)
f表示式(2)~式(5)的非线性关系。式(6)描述了地层随井深的变化,同时还需要建立反映测量信息与状态变量间的对应关系的测量方程。
1.2 最优测量方程的建立
设长、短道源采集的核脉冲的个数X1(h)和每个脉冲的能量X2(h)的测量计数率为Z(h),设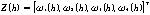 ,则其关系可表示为:
,则其关系可表示为:
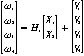
(7)
由于增广的状态为4个,最后测量矩阵为4×4阶矩阵。
测量方程为:
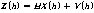 (8)
(8)
式(7)反映了状态变量式(6)与测量方程式(8)之间的对应关系。由于状态方程式(6)是非线性的,而测量方程式(8)是线性的,所以需要采用广义卡尔曼滤波对测量方程(8)进行滤波更新。
下面用状态方程和系统测量方程结合它们的协方差来估算系统的最优化输出。利用过程模型来预测下一状态的系统。假设现在的系统状态是k,根据系统的模型,可以基于系统的上一状态而预测出当前状态[4-5]:

式(9)中,状态微分方程组右端项;T表示系统的采样间隔;其中:
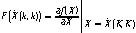 (10)
(10)
至此,系统结果已经更新了,对应于的协方差的更新如下(用P表示协方差):
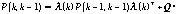 (11)
(11)
式(11)中Qn表示 W(k)动态噪声的协方差矩阵;λ(h)T表示λ(h)的转置矩阵,且:
 (12)
(12)
其中,I为单位矩阵。
式(9)、式(11)即是对系统的预测。
结合当前状态的预测值和当前状态的测量值,得到现在状态k的最优化估算值X(k,k):
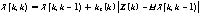 (13)
(13)
式(13)中,kg表示卡尔曼增益(Kalman Gain):
 (14)
(14)
式(13)、(14)中,H表示测量矩阵;Rm表示测量噪声的协方差矩阵。
为使卡尔曼滤波器不断地运行下去直到系统过程结束,再对k状态下X(k,k)的协方差进行如下更新:
 (15)
(15)
式(9)~式(15)是对测量方程(8)的滤波更新,即得到最优测量方程。结合式(6)~式(8)以及设定的参数即可对谱图进行滤波。
2 测量方程的参数设计
以上递推公式中,需要设计式(7)以及式(9)~(15)中的参数。式(7)中,V1~V4为测量噪声,H矩阵为4×2阶测量矩阵,可由现场的标准刻度井测量数据来确定。需要说明的是,每个测井仪器都有一套自己的H矩阵,它可认为是不随其他因素变化而变化的常数矩阵。本文中,H1取为:
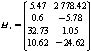
根据所建立的系统模型式(2)~式(6)以及式(8),对方程进行离散线性化处理,则有:

(16)

(17)

(18)
式(16)~式(18)是式(9)~式(15)的设计参数,其中missing image file分别是W1(h)~W4(h)的方差,均值为0。missing image file分别是V1(k)~V4(k)的方差,均值为0。
3 实测滤波情况
结合以上递推公式,在给定滤波初值(即X(0))后,估计误差协方差矩阵初值P(0,0)、采样间隔T以及协方差阵(Qn,Rm),即可以滤波。
在核脉冲全谱数据采集系统中,其控制量为仪器中直接贴于NaI晶体端面的一种低强度137Cs源,137Cs源发射的662 kev射线直接进入晶体,γ衰变是核现象,与温度无关,故与之相对应的电子脉冲信号应维持恒定幅度,并以其为参考值调整高压,在谱图处理中,它可以认为是常数[6],谱图对比不受影响。
由于在测井过程中,仪器运动速度快,所以核脉冲采集周期一般为20 ms或40 ms。在本文设计中,核脉冲的采集周期为40 ms ,即ΔT=40 ms。测试取一帧的数据,即256道谱图。
本文对实验数据进行了处理,在相同的实验数据下,分别对硫、铝进行测试对比,通过长、短源谱图滤波,对卡尔曼滤波谱图与深度加权滤波谱图进行比较,具体谱图波形见图1~图4。

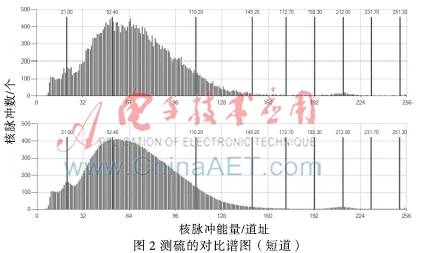
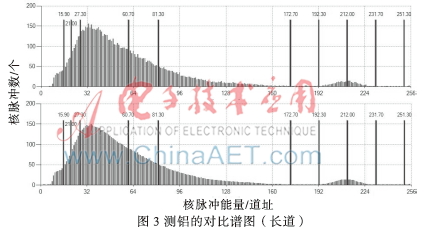
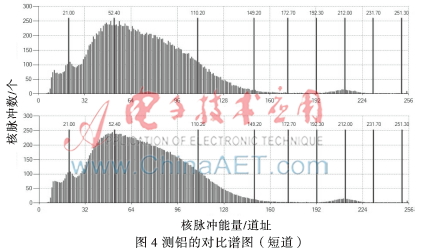
图1~图4中,齐的黑线如15.90、27.30等是参考道址,为了方便观察谱图是否滞后,便于对比。道址192.30~265之间是稳谱峰图,主要是为了增加分布在0~192.30道址之间核脉冲的能量强度,便于突出异同,在计算解释谱图时会去掉,计算不受影响。
图1~图4中,上图是深度加权滤波得到的谱图,下图是卡尔曼滤波得到的谱图,通过上下图的对比可以看出,下图的包络明显趋向平滑,能够有效消除统计涨落的影响。通过两组对比可以看出,在相同的实验数据下,此卡尔曼滤波得到的谱图比深度加权滤波得到的谱图包络线更接近于平滑,有力消除了谱图的统计涨落,更利于测井数据的分析。
4 结论
文中通过对核脉冲全谱数据采集系统的解谱需求,设计了一种卡尔曼函数滤波器,通过实验谱图对比可以看出,其包络线几乎接近于平滑,消除了谱图的统计涨落,提高了光滑度。说明了本文所设计的卡尔曼滤波对谱图处理的有效性和可行性。
参考文献
[1] 彭晓光,柏林,田彦民,等. 基于FPGA的全谱岩性密度数据采集系统[J]. 核电子学与探测技术, 2012,32(7):758-760.
[2] 邵玉华. 卡尔曼波形估计在雷达信号处理中的应用[J]. 黑龙江科技信息, 2012(2):77.
[3] 彭丁聪. 卡尔曼滤波的基本原理及应用[J]. 软件导刊, 2009(11):33-34.
[4] 张永伟,杨锁昌,张敏,等. 卡尔曼滤波在落点偏差预测算法中的应用[J]. 中国测试, 2012,38(s1):112-113.
[5] 黄亚萍. 基于卡尔曼滤波的抑制NLOS定位算法研究[J]. 电信快报, 2012(4):48-51.
[6] 彭晓光. 新型全谱岩性密度测井仪的研制[D]. 邯郸:中船重工718研究所, 2012,44-47.

