0 引言
　　在处理包含数模转换(DAC)器件的电路输出信号时，由于DAC器件采样频率有限特点，输出信号在时域内成阶梯状，从频域角度看，将得到复杂的谐波分量[1-2]。其中包含的高频干扰分量特别容易与电子线路发生电磁耦合，如果不采取有效的抑制措施，将会严重影响信号的质量，甚至将引起电磁辐射干扰。因此，设计一个性能良好、能对带外无用频谱具有抑制功能的滤波器，成为了DAC硬件电路首要任务。
　　然而伴随着硬件技术的发展，DAC采样率的逐渐提高，传统单端模拟电路无法胜任高采样的需求，如今已逐渐被具有差分结构的模拟输出电路所替代。但是，通常处理差分结构模拟输出信号的普通差分滤波器在高频抑制能力却较差，不能达到高品质要求[3-4]。
　　为此，综合差分结构抑制共模干扰的对称性与接地电容抑制高频干扰的有效性，设计一种多处电容接地差分形式的巴特沃斯滤波器。通过仿真与实测实验对低频滤波性能和高频干扰抑制性能进行测试评估。结果表明，多处接地差分形式低通滤波器的低频滤波效果与高频干扰抑制性能都优于普通差分滤波器。
1 巴特沃斯设计原理
　　1.1 巴特沃斯低通滤波器幅频特性[5]
　　巴特沃斯低通滤波器的幅度平方函数：
　　

　　其中，n为滤波器阶数，?棕c为滤波器的截止频率。根据式(1)，用MATLAB仿真得出1～5阶巴特沃斯滤波器幅频特性曲线，如图1所示。

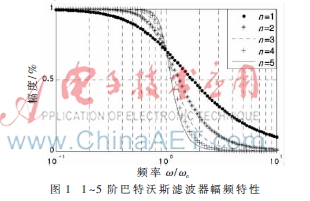
　　1.2 传递函数
　　

　　令分母多项式等于零，解算极点得：
　　
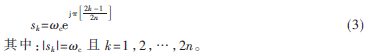
　　由推导结果可得，巴特沃斯滤波器传递函数2n个极点均匀分布间隔，第1个极点位置　　又因滤波器稳定，故取左s平面的全部极点作为H(?棕)的极点，右s平面是的极点属于H(-?棕)，结合式(2)幅度平方函数得：
　　　

  　n为偶数时：
　　

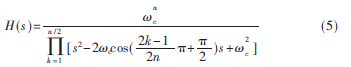
　　n为奇数时：
　　

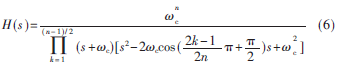
　　将传递函数归一化处理，令s=s/，则将s=s·c代入传递函数表达式可得：
　　n为偶数时：
　　

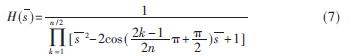
　　n为奇数时：
　　

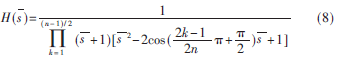
　　其通式为：
　　

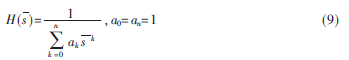
　　通过查归一化多项式表（表1）可得参数ak，计算出传递函数通式H(s)，将s=s/c代入H(s)得标准传递函数H(s)，最后对H(s)进行电路配置即得所需滤波器。差分形式滤波器只需在完成配置的单端电路基础上，保持单端滤波器电路中电容值固定，并将电感平均分配到差分电路的两条支路中即可完成配置。
　　1.3 接地电容效果分析
　　在电路中电容C容抗值Zc=1/2fC，且容抗随着频率f的增大而减小。因此滤波器电路中一个恰当的接地电容C，可使交流信号中的高频成分通过电容落地，而低频成分可以几乎无损失通过，故将小电容接地等同于设计一阶低通滤波器。在滤波器电路中，多处电容接地设计等同于多个低通滤波器与原电路组成低通滤波器网络，在提高截止频率附近幅频特性的同时会较好抑制高频干扰，因而接地优化在理论上是可行的。
2 滤波器设计仿真
　　根据实践需要，设计满足上级输出电路阻抗为100 、下级输入电路阻抗为50 、截止频率为5 MHz的5阶巴特沃斯低通滤波器。普通差分滤波器由于其极点与单端滤波器极点相同，故具有相同的传递函数，因而依据单端滤波器配置的差分结构滤波器能够满足指标要求。在差分结构形式上进行接地优化后，由于接地电容具有低通滤波功能，不同电容值C会导致不同频段幅频响应迅速衰减。图2～图5分别为普通差分滤波器与多处接地差分滤波器的配置电路与幅频特性曲线。

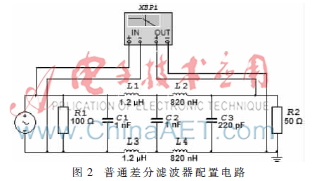
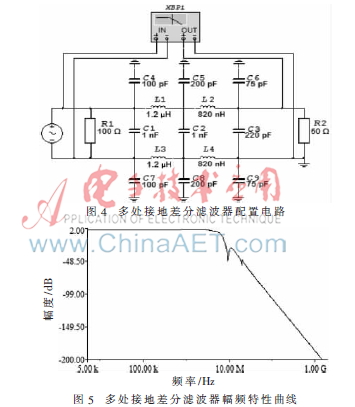
　　由仿真结果可得，截止频率为5 MHz的多处接地差分滤波器幅频响应在9 MHz内迅速衰减至-50 dB，而后在10 MHz处上升为-30 dB；而普通滤波器幅频特性在9 MHz处为-20 dB，在10 MHz处为-22 dB。因此，接地优化滤波器幅频特性曲线总体位于普通差分滤波器幅频特性曲线形成的包络内，故多处接地达到了过渡带变窄与抑制高频的效果，因而接地优化电路设计通过仿真是可行的。
3 实物验证与分析
　　由于实际电路与理想条件有一定差异，可能导致实际效果与仿真结果不符，为验证接地优化差分滤波器，在实际电路中能够提高截止频率附近幅频特性与抑制高频干扰的能力，将上一节仿真通过的普通差分滤波器与接地差分滤波器制作成PCB电路，通过矢量网络分析仪测试其频率特性，结果如图6～图9所示。

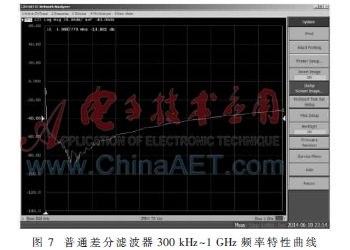
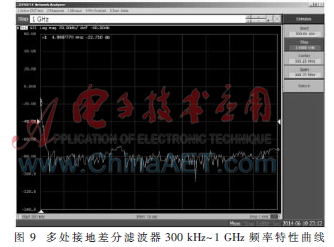
　　由图可得，多处接地差分滤波器电路中，由于接地电容相当于一阶低通滤波器，所以由接地电容与普通差分滤波器组成低通滤波网络能够大幅提高滤波器截止频率附近幅频特性。同时，由于容抗Zc=1/2fC随f增大而减小，在高频时几乎为零，高频信号可以通过电容落地，故其在高频抑制能力上大大优于普通滤波器。因而接地优化在实际电路应用中是真实有效的，可以应用于抑制高频信号的低通滤波器中。
4 结论
　　多处接地差分形式滤波器，由于其接地电容相当于低通滤波器，故只要其容抗值Zc=1/2?仔fC能够小于等于电容单独作为一阶低通滤波器时截止频率要求的容抗值，就可以大大提高滤波器截止频率附近幅频特性与抗高频干扰的性能,这为具有差分结构的DAC成型滤波器的设计提供理论指导作用。
参考文献
　　[1] 刘朝军，许人灿，陈曾平.DDS输出信号频谱结构的系统分析[J].国防科技大学学报，2005，27(6)：53-56.
　　[2] 刘兰坤，潘明海.DDS的杂散分析及降低杂散的方法[J].电子器件，2007，30(2)：572-574，578.
　　[3] 毛敏，郑珍，周渭.基于DDS的低通滤波器的设计与实现[J].电子科技，2006(3)：17-20.
　　[4] 陈跃，田书林，刘科.非理想DDS输出信号分析及滤波处理[J].电子质量，2008(9)：4-7.
　　[5] 张金玲.电磁干扰低通滤波器的设计[J].中国科技信息，2008(20)：162-164，168.