文献标识码: A
文章编号: 0258-7998(2014)11-0109-04
0 引言
为了提高卫星通信的频谱资源占用效率和通信质量,调制体制的频谱效率和调制信号的峰值平均功率比越来越受到关注。由于卫星信道既是带宽和功率受限信道,又是非线性信道,需要具有已调载波功率谱密度比较集中的调制方式,因此通常采用恒包络调制。在恒包络调制中广泛采用相移键控(PSK)方式。然而由于PSK相位不连续,导致了较大的带外功率泄漏。相对于传统的MQAM调制,圆环形信号星座的MAPSK调制将信号幅度限定在很少的几个取值,因此具有更低峰值平均功率比,有效地降低了非线性的影响,所以更加适合非线性信道的通信[1]。所以近二十年来,越来越多的卫星通信都开始推荐采用MAPSK调制体制,其中最具有代表性的就是第二代卫星数字视频广播系统[2](DVB-S2)。与MQAM调制相比,MAPSK便于实现变速率调制,因而很适合根据信道及业务需要分级传输的应用,所以在国际空间数据系统咨询委员会(CCSDS)发布的131.2-B-1:2012《适用于高速率遥测应用的灵活先进的编码调制技术》也推荐采用MAPSK调制方式作为高速遥测的制式标准。
MAPSK作为非常具有竞争力的卫星通信调制方式,吸引了科学家们的研究兴趣。按优化的目标函数不同,可以将目前关于MAPSK的星座图优化的方法主要分3类:第一种是以符号互信息函数为目标函数的优化设计[3-4];第二种是以星座图上的最小欧氏距离最大化为目标函数的优化设计[5];第三种是在没有任何先验知识(对星座图的结构以及比特和符号之间的映射方式没有任何先验知识)的情况下,对比特互信息函数进行优化,其中包括了使用模拟退火算法[6]和遗传算法[7]等两大类。
在国内外相关研究中,没有涉及到与解映射结合的星座图的优化方法。本文提出与低计算复杂度解映射的方法相结合,以星座图上距离解映射门限的最小距离的最大化为目标函数来进行优化设计,就对这种思路做出了一种探索。为了具体说明和讨论的方便,本文下述部分以16APSK为例来进行说明,即在4+12-APSK的星座结构进行探讨。正如参考文献[8]中提到,4+12-APSK在具有和16QAM相近的误码特性的同时,也具有和16-PSK一样的抵抗非线性的能力,所以选择4+12-APSK作为16-APSK的星座结构是一个很好的折衷。对于采用比特交织编码调制(BICM)结构的系统,解映射输出的软解调信息直接关系到信道译码的优劣。目前实际应用中普遍采用的解映射算法Log-Likelihood比值法、Log-Map算法以及Max-Log-Map算法的计算复杂度都比较高,特别是当调制阶数较高时,给FPGA的资源占用和逻辑的复杂度都提出了巨大的挑战。高复杂度的算法不但消耗系统资源、延长开发周期,而且在复杂逻辑下,更容易寄生信号的竞争和冒险。本文从工程实现的角度考虑,以简化实用的软解调算法为基础,提出与之结合的星座优化设计。
1 16APSK调制
1.1 16APSK信号星座
MAPSK调制方式的星座图通常由多个同心圆共同组成[9],在每个同心圆均分布着多个信号点,这些信号点构成的信号集可以表示为:
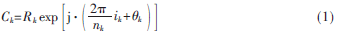
式中,Rk为第k个同心圆的半径, 为星座图中信号的相位,nk为第k个同心圆上的信号点数,k为第k个同心圆上的信号的初始相位,ik(ik=0,1,…,nk-1)为第k个同心圆上的一个信号点。在信号星座图的单个圆上的信号点都是按M-PSK进行排列的。伪格雷码映射的4+12-APSK信号星座图如图1所示,其中横坐标I表示实部,纵坐标Q表示虚部。
为星座图中信号的相位,nk为第k个同心圆上的信号点数,k为第k个同心圆上的信号的初始相位,ik(ik=0,1,…,nk-1)为第k个同心圆上的一个信号点。在信号星座图的单个圆上的信号点都是按M-PSK进行排列的。伪格雷码映射的4+12-APSK信号星座图如图1所示,其中横坐标I表示实部,纵坐标Q表示虚部。

1.2 卫星非线性信道特性对16APSK的影响
为了充分提高星载功率的效率,卫星转化器内的高功率放大器一般都工作在邻近饱和点附近,TWTA-HPA非线性会引入信号的幅度和相位的变化:
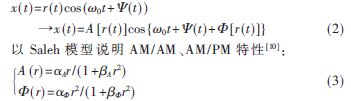
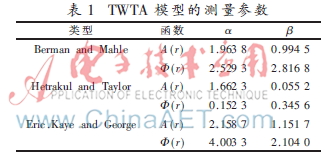
其中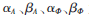 为模型的4个参数,r为信号星座图上的半径(亦可等效为功率量纲)。对于不同信道的不同非线性度,采用不同的参数来表征。表1列出了TWTA模型的测量参数[11-12]。
为模型的4个参数,r为信号星座图上的半径(亦可等效为功率量纲)。对于不同信道的不同非线性度,采用不同的参数来表征。表1列出了TWTA模型的测量参数[11-12]。
对于16APSK调制,考虑TWTA-HPA的非线性会使信号星座图的内外环信号点发生相对旋转和半径的缩放:
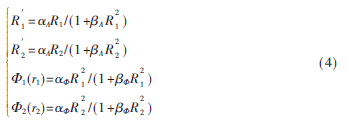
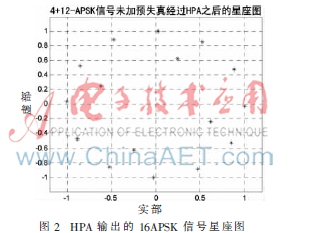
对于16APSK,在未加预失真技术的情况下,标准星座分布的信号在经过TWTA-HPA后的星座图如图2所示,此处所采用的是Eric.Kaye and George测量参数。
从上面的图分析可知,TWTA-HPA的非线性会使得卫星通信的质量严重下降。为了尽可能地克服信道的非线性影响,在星座图的优化设计中加入预失真的方法;对卫星的信号星座进行预失真,使得信号通过TWTA-HPA之后恢复成没有失真的理想的星座分布,以此来提高在非线性信道中的通信质量。设R分别表示优化设计后的信号半径和初始相位(也就是加入预失真,通过TWTA-HPA应该得到的半径和相位),则预失真后的半径和相位可以表示成:
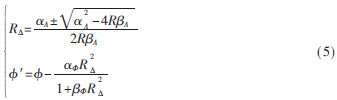
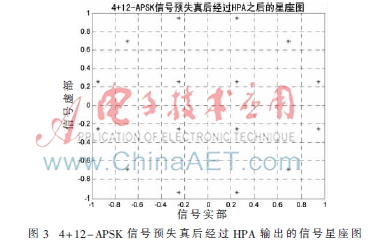
其中R分别表示预失真后的信号半径和初始相位。加入预失真后,以Eric.Kaye and George为测量参数的TWTA-HPA模型仿真输出星座如图3所示。
2 简化的解映射方法
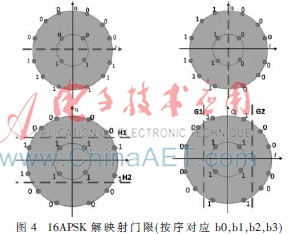
目前常用的16APSK的解映射算法有最大似然法、MaxLLR、相位和幅度结合硬判决法。但是它们的计算量较大,且涉及到除法和反正切运算,不适合在FPGA中实现。结合一种只用幅度大小实现软解调的方法来优化MAPSK星座图[13]。对图1按比特分割成4个子星座图,如图4所示。对应的解映射门限的数学表达式如下:
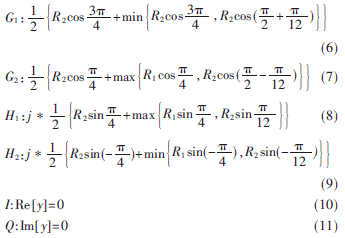
对应的bi,i∈(0,1,2,3)的软输出信息LLR(bi)为:
LLR(b0)≈-Re[y](12)
LLR(b1)≈-Im[y](13)
LLR(b2)=|G1|-|Re[y]|(14)
LLR(b3)=|H1|-|Im[y]|(15)
该简化算法和传统的最大似然法、MaxLLR算法以及基于幅度和相位的硬判决算法的复杂度比较如表2所示。由表中可以看出,本文提出的解映射算法将16APSK的解映射的计算量大大减少。

3 与解映射相结合的优化
从上图可以看出,当接收的符号在星座图上的位置越靠近解映射门限,虚警概率会增大。反之,当接收的符号在星座图上的位置越远离门限电平,则虚警概率越低,所以正确译码的概率就越大。为了方便后面的讨论,把式(1)中的关键参数用相对值表示,而非绝对值。定义外环相对于内环的相移;外环相对于内环的半径比?籽2=r2/r1。结合16APSK的星座图的约束,将优化的目标函数表示如下:
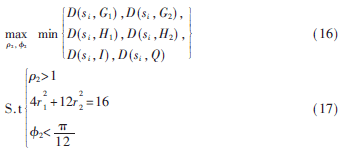
4 仿真结果
4.1 星座优化设计仿真
将星座图的优化目标函数设定为星座图上与解映射门限的最小距离的最大化。用穷举搜索的方法得出16APSK的内外半径之比和星座图上与解映射门限的最小距离的变化,如图5所示。
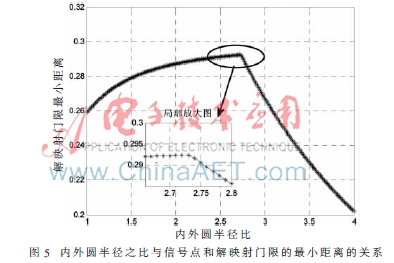
考虑16APSK内外环之间发生相对旋转的情况下,内外半径之比和星座图信号点与解映射的门限之间的最小欧氏距离的变化关系如图6所示。
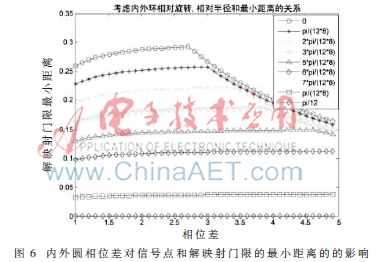
综合上面的仿真结果,在所提出的简化的解映射算法下的星座图的内外半径最优比是2.73,初始相位差为0。该优化函数对内外环的相差很敏感。因为初始相位差越小,星座图的旋转越小,导致判决门限和坐标轴的垂直度越好,这样I、Q两路的独立性越好,故而能够得到好的结果。
4.2 优化目标下的解映射性能仿真
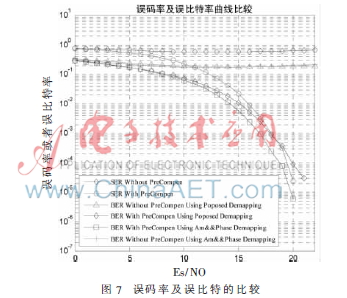
考虑到卫星信道的非线性对通信质量的影响,在仿真中加入了预失真技术。从图7的仿真结果看出,在加入了预失真技术之后的误码性能明显优于未加预失真技术的误码性能。本文简化后的解映射技术与传统的基于幅度和相位的解映射的性能相比,在相同的误比特率为10-4的情况下,信噪比相差约1 dB。
参考文献
[1] 徐烽,邱乐德,王宇.基于精简星座鉴相的大频偏16-APSK信号载波同步[J].电子技术应用,2013,38(12):87-89.
[2] Framing structure,channel coding and modulation for a second generation digital terrestrial television broadcasting system(DVB-T2),ETSIEN 302 755 Std.,Sep.2009.
[3] LIOLIS K P,ALAGHA N S.On 64-APSK constellation optimization[C].Signal Processing for Space Com-munications,10th International Workshop on,2008.
[4] Qiu Chunhui,Liu Xuming.Optimal design of amplitude phaseshift keying constellation for satellite communications[C].Electric Information and Control Engineering(ICEICE),2011International Conference on.2011.
[5] Chen Xudong,Yang Huazhong.Optimization of MAPSK[C].Advanced Communication Technology,2009.ICACT 2009.International Conference on,2009.
[6] KAYHAN F,MONTORSI G.Joint signal-labeling optimiza-for pragmatic capacity under peak-power constraint[C].Global Telecommunications Conference (GLOBECOM 2010),2010 IEEE,2010.
[7] Yan Keqian,Yang Fang,Pan Changyong,et al.Genetic algorithm aided gray-APSK constellation optimization[C]. Wireless Communications and Mobile Computing Conference (IWCMC),2013 9th International,2013.
[8] De Gaudenzi R.Performance analysis of turbo-coded APSK modulations over nonlinear satellite channels[J].Wireless Communications,IEEE Transactions on,2006,5(9):2396-2407.
[9] Seung Hyun Choi,Cheon In Oh,Doeck Gil Oh,et al.The mapping and de-mapping algorithms for high order modula-tion of DVB-S2 systems[C].APCC′06,Asia-Pacific Confer-ence on Communications,2006:1-5.
[10] SALEH A A M.Frequency-independent and frequency-dependent nonlinear models of TWT amplifiers[J].Commu-nications,IEEE Transactions on,1981,29(11):1715-1720.
[11] KAYE A,GEORGE D,ERIC M.Analysis and compensa-tion of bandpass nonlinearities for communications[J]. Com-munications,IEEE Transactions on,1972,20(5):965-972.
[12] 张敏,景占荣,郭淑霞.卫星非线性信道下非对称MAPSK优化设计[J].电子技术应用,2012,38(4):98-101.
[13] 代宜君.卫星高效编码调制体制设计[D].西安:西安电子科技大学,2010.

