0 引言

    现代数控系统、工业机器人正向着高速和高精度的方向发展，而加减速控制算法在实现其运动的高速、高精度上起着至关重要的作用。哈尔滨工程大学郑金兴等^[1]提出了基于梯形速度控制的变插补周期实时插补算法，该算法可有效地控制加工精度，充分发挥了各轴联动的加减速能力，但在运动的高速和实时性上不是很理想；朱明等^[2]提出了一种实用的S曲线加减速控制算法，该算法加速度连续变化，速度变化平稳，减小了加工过程中速度突变造成的冲击,但算法稍复杂，计算量大。目前，应用于数控系统和工业机器人中的加减速运动控制算法有很多。如梯形曲线加减速、S形曲线加减速、多项式加减速、三角函数加减速^[3-4]等控制算法。这些加减速算法都可以通过软件编程的方式实现，但由于计算量较大使得很难通过硬件编程的方式实现。为了减小计算量，实现加减速控制算法的高速与高精度，Chen和LEE^[5]提出了基于FIR滤波器的加减速速度规划算法。该算法采用滤波技术对加减速度进行光滑处理，实现了加减速的连续变化，减少了加工中由于加减速突变而产生的振动，进而实现高精度加工，同时又能达到良好的加减速性能，实现高速的加工；但其算法稍复杂，实现上有一定的难度。KIM D^[6]提出了一种基于卷积的加减速运动规划算法。该算法通过对速度进行卷积，使得在计算过程中只包含加法与除法运算，简化了复杂的计算过程，提高了加减速控制算法的运算速度。

    本文在以上研究基础上，引入数字卷积，采用FPGA硬件编程的方式实现数字卷积加减速控制算法，提高了运算速度与精度。该算法采用定点数进行计算，节约了FPGA的逻辑门的数量并且减小了计算误差。

1 数字卷积加减速算法

    基于数字卷积加减速算法[7]卷积算子表达式为：

    由于式(2)是迭代表达式，并且只包含加法和除法运算，因此采用FPGA硬件去实现将极大地降低计算量。

    对于固定速度V_max输入经过一次数字卷积后得到如图1所示的梯形加减速曲线。其中，总的运行时间nT_s等于曲线的长度除以固定速度V_max。经过数字卷积后速度的位移距离必须保持一致，因此，H₁的值取为1/n₁T_s。如果想要得到光滑、高柔性的S形加减速速度曲线，可以对固定速度输入进行两次数字卷积，即对得到的梯形速度曲线再进行一次数字卷积如图2所示。另外，为了确保在经过两次数字卷积后能够达到最大速度V_max，n₂T_s的时间必须小于n₁T_s，否则在经过数字卷积后得到的最大速度将小于固定的速度值V_max。

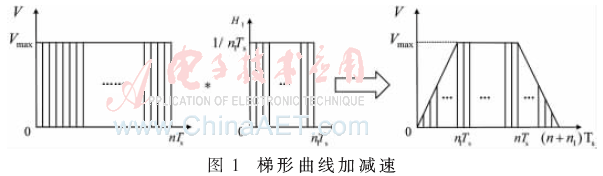
2 数字卷积加减速算法的硬件实现

2.1 梯形加减速算法的实现

    对于单轴点对点的梯形加减速运动，S为总的运动距离，V_max为最大速度，N₁为梯形加减速数字卷积序列长度。总的运行时间为S除以V_max；在FPGA硬件设计时采用定点数进行计算，在运算过程中涉及到除法运算。因此，为了减小误差要考虑余数的问题。文中的运动距离S、速度V_max及余数之间的关系表达式如式(3)：

    其中，N表示速度为V_max时的速度序列脉冲数，R为余数。另外，输入速度序列为X₁[k]，如图3所示。

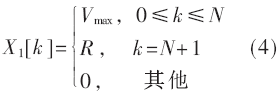
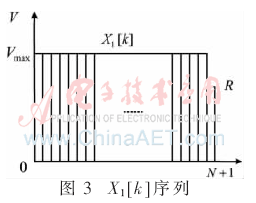
    卷积算子序列Y₁[i]如图4所示，数字卷积序列长度为N₁，其中N₁<N/2。通过对X₁[k]与Y₁[i]进行一次数字卷积得到梯形加减速运动控制速度序列如图5所示，其表达式为式(5)：

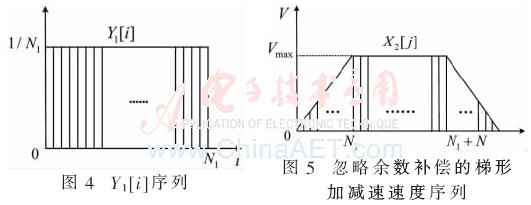
    如果忽略余数R，在运动过程中将出现速度误差，进而导致位置误差。为了解决这个问题，本文采用速度补偿的方式，在速度序列的末尾添加补偿速度序列来消除余数误差，得到的速度输出序列如图6所示。

2.2 S形曲线加减速算法的实现

    如果对X₁[k]进行两次数字卷积将得到S形加减速曲线；对于S曲线加减速，第二次数字卷积的序列长度为N₂。为了保证在经过两次数字卷积后，能够达到最大速度V_max，N₂的取值必须小于N₁，卷积算子序列Y₂[n]如图7所示。通过X₂[j]与Y₂[n]进行数字卷积可得到S形加减速曲线速度序列X₄[q]，如图8所示。

    与梯形加减速类似，如果忽略余数R将导致速度误差和位置误差。为了解决这个问题，本文采用速度补偿的方式，在速度序列的末尾添加补偿速度序列来消除余数误差，得到的速度输出序列X₅(h)如图9所示。

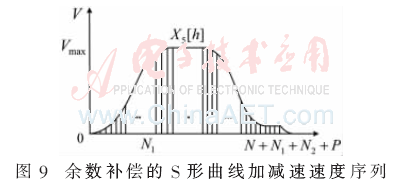
2.3 余数补偿算法

    由于在通过FPGA实现的过程中采用定点数进行计算，因此，在卷积计算的除法运算过程中，需要考虑余数问题^[8]。事实上，在整个数字卷积的计算中有两种情况会产生余数：第一种情况是在数字卷积之前卷积序列长度N的计算，如式(3)所示；另一种情况是在数字卷积计算过程中产生的余数如式(2)所示。为了解决上述问题，针对不同情况下的余数问题采用不同的算法来实现补偿。

    对于在数字卷积之前产生的余数，余数R的计算如式(3)所示，这种情况下采用在速度序列的末尾添加速度补偿序列。梯形加减速的卷积序列X₂[N₁+N-1]如式(5)所示，余数R可表示为：

    其中，V是X₂[N₁+N-1]序列的值；A表示速度为V时的速度补偿序列脉冲数；B表示最终补偿脉冲序列的误差值。另外，P表示在图7中总的添加的补偿速度序列脉冲数。

    类似地，对于S形曲线加减速速度序列X₄[N+N₁+N₂-1]如式(6)所示，余数R可以表示为：

    其中，W是X₄[N+N₁+N₂-1]序列的值；C表示速度为W时的速度补偿序列脉冲数；D表示最终补偿脉冲序列的误差值。另外，P表示总的添加补偿速度序列脉冲数。

3 仿真与验证分析

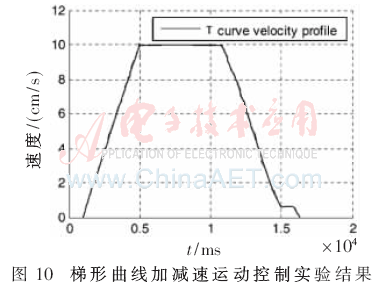
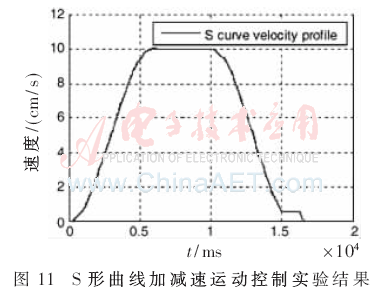
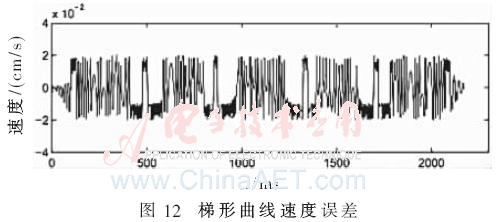
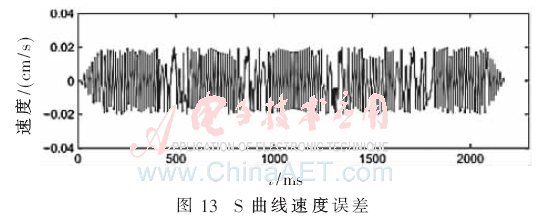
    仿真验证过程在Matlab和Quartus II 13.1开发环境下采用硬件描述语言Verilog，在Altera的Cyclone IV器件上进行仿真和验证实现。图10为在MATLAB上S=250，V_max=10，N₁=7时的梯形曲线加减速运动控制实验结果；图11为S=250，V_max=10，N₁=7，N₂=4时的S形曲线加减速运动控制实验结果；图12、图13分别为梯形和S形曲线加减速速度误差图，从图中可以看出速度的误差保持在±0.02范围内。图14为S=250，V_max=10，N₁=7时的梯形曲线加减速通过FPGA硬件实现后在Modelsim上的仿真波形图，图15为S=250，V_max=10，N₁=7，N₂=4时的S形曲线加减速通过FPGA硬件实现后的仿真波形，其中，标有圆圈部分为添加的余数补偿速度部分。

4 结论

    针对工业机器人、数控系统中的加减速控制算法引入了数字卷积，减小了计算量，并通过FPGA硬件编程的方式实现了数字卷积的梯形曲线、S形曲线加减速控制算法。本文详细分析了采用定点数计算数字卷积加减速算法过程的余数的处理方式。对与数字卷积运算之前产生的余数，在速度序列的末尾添加速度补偿序列来消除余数误差；对于数字卷积运算过程中产生的余数，采用余数累加的方式，来减小余数误差。采用FPGA硬件编程的方式实现加减速控制算法，简化系统结构，提高运算效率和算法的稳定性。

参考文献

[1] 郑金兴，张铭钧.梯形速度控制变插补周期的实时插补算法研究[J].机床与液压，2007(1)：77-80.

[2] 朱明，游有鹏，何均.S形加减速算法前瞻处理研究[J].小型微型计算机系统，2011(10)：2140-2144.

[3] 陈晓兵，廖文和.基于分段刀轨S曲线加减速控制的进给速度优化研究[J].组合机床与自动化加工技术，2012(10)：44-47.

[4] 刘筱，吴文江，郑飂默.柔性S型加减速控制算法研究[J].组合机床与自动化加工技术，2014(3)：66-68.

[5] CHEN C S，LEE A C.Design of acceleration deceleration profiles in motion control based on digital FHR filters[J].Journal of Machine Tools & Manufacture，2001，38：799-825.

[6] KIM D I，JEON J W，KIM S.Software acceleration/deceleration methods for industrial robots and cnc maching tools[J].Mechatronics，1994，4(1)：37-53.

[7] 陈伟娜，赖乙宗，李松，等.数控系统线性加减速算法分析与实现[J].科学技术与工程，2012(3)：546-550.

[8] 王昕，王均伟，饶志，等.基于NURBS曲线轨迹规划与速度规划的研究[J].系统仿真学报，2008(15)：3973-3980.