0 引言

    在室内传播环境中，电磁平面波常常从各个方向伴随着不同的传播延迟到达接收天线，这种现象是由墙壁、家具等障碍引起的反射、衍射、散射所造成的。未来室内无线通信系统的一个重要特征是它们比现在的系统占据了大得多的带宽，因此，移动衰落信道必须根据频率选择性建立信道模型。文献[1]中提出的经验统计模型，是根据在特定的室内环境中所收集的测量数据开发的。这种模型的缺点是其特性受限于特定的传播环境。文献[2]中基于光线追踪技术的方法，用来模拟特定室内传播场景，这种方法的准确性只能在计算复杂度时得到保证。文献[3-4]中针对室外传播场景研究了相对于频率选择性窄带几何信道模型的一个扩展。

    本文通过进一步扩展几何矩形散射模型来建立室内宽带移动衰落信道模型，目前这种方法已经在文献[5]中被提出来表征室内传播环境特性。本文通过假设无限数量的散射体均匀分布在三维房间的二维(2D)水平面上，着重研究室内宽带信道参考模型统计特性。文中推导到达角(Angle of Arrival，AOA)概率分布函数(Probability Density Function，PDF)、功率延迟分布(Power Delay Profile，PDP)、频率相关函数(Frequency Correlation Function，FCF)的解析表达式。本文还根据参考模型提出了一种SOC信道仿真模型。结果表明，本文所设计的SOC信道仿真模型相对于频率相关函数与基本参考模型相符，同时这种SOC信道仿真模型能够模拟室内移动衰落信道，减少实际支出。

1 室内几何散射模型

    几何散射模型的首次提出是在文献[5]中，用来表征室内传播环境特性。文中选取三维房间的一个2D水平面，因此在本文中假设无数的散射体、基站(Base Station，BS)和移动台(Mobile Station，MS)位于二维(Two Dimensional，2D)平面。

    如图1所示，这个矩形代表房间的2D水平面，其长和宽分别由A和B表示。基站为信号发射器，移动台为信号接收器，假设移动台沿着x轴的方向移动。此外，考虑单一反弹散射，这表示从基站发射的波达信号平面波到达移动台之前仅通过一次散射体反弹。

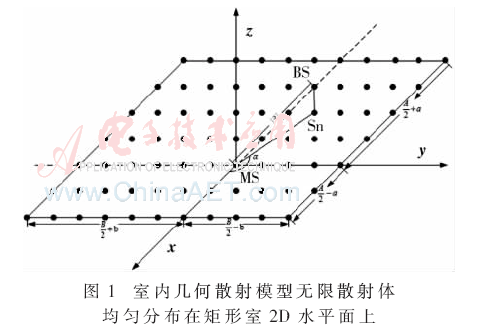
    图1中黑点代表平面中散射体位置，在现实世界中，散射体的数目和它们的位置在不同传播场景中都是不同的。本文研究的是所有可能性传播场景中的一个平均、普通的统计模型。文中假定无限数量的散射体均匀分布在一个矩形室的二维水平面上。该模型通过使用SOC的原理可用于推导高效信道模拟器，实现成本比较低。

2 信道统计特征分析

    下面研究本文提出的室内宽带参考信道模型的统计特性，特别是到达角(AOA)概率分布函数(PDF)、功率延迟分布(PDP)、频率相关函数(FCF)。

    从图1可以看出，基站放置于(c，0)(c≤0)，同时移动台位于坐标系的原点。波达信号到达角AOA通过?琢表示，所有的散射体S_n(n=1，2，…，N)均匀分布在房间的二维水平面上。散射体的位置由(z，α)用极坐标形式表示。根据文献[5]，联合概率分布函数p_zα(z，α)可以表示为：

    通过运用随机变量转换的基本原理^[6]，可以得出联合概率分布函数p_Dθ(D，θ)，表示为： 

2.1 平面波最大行进距离D

    式(2)描述了平面波从基站BS出发经过一个矩形房间内2D水平面上任意地方的散射体到移动台MS的行进距离。函数D(z，α)的导数与z相关且是正值，导数如下：

    可以看出D_max(α)取决于到达角α。根据式（9），可以得到图2。

2.2 到达角概率分布函数（PDF）

    根据式(6)推导到达角概率分布函数，这里将所有的传播延迟定义为： 

2.3 功率延迟分布（PDP）

    行进距离D的概率分布函数可以通过p_D(D)表示，计算方程为：

2.4 频率相关函数（FCF）

3 数值结果与分析

    通过对式（13）、式（18）的数值分析，给出了理论结果，通过计算机仿真验证了本文结论。假定选取长度A=10 m和宽B=5 m的房间作为室内参考环境。参数a和b分别选择2和1。

    图3为宽带参考信道模型到达角的概率分布函数的仿真结果，其中选取了两个不同的基站位置，c=-2和c=-4。从图中可看出到达角的概率分布函数的大小与基站BS的位置无关。从散射体的位置开始计算到达角和传播延迟，接着根据所获得的到达角的随机值求出到达角AOA的概率分布函数图3还给出了窄带信道模型到达角的概率分布函数，可以看出在相同的室内环境情况下，宽带信道模型到达角概率分布函数与窄带模型的一种情况相一致。

    图4所示频率相关函数的绝对值，文中通过不同的矩形室长度A的值，运用式（18）计算出频率相关函数的绝对值。为了比较结果，通过文献[3]中的式（18）在图4中画出了频率相关函数的理论曲线。这里取ζ=10作为SOC信道模拟器的传播路径^[7]。根据文献[6]中提到的方法将功率分配到不同路径。SOC信道仿真模型的到达角通过采用相同面积的改良方法计算得出。从图4可以看出，SOC信道仿真模型的频率相关函数与参考模型相当一致。当房间长度A从10 m增加到30 m时，随着频率间隔v′的增加，频率相关函数下降的越来越快。同时，随着A的增加，相干带宽B_c变得越来越小。

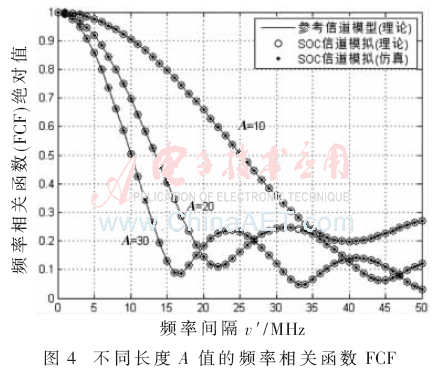
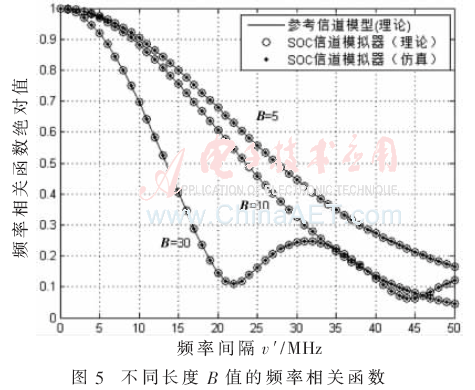
    图5所示为房间宽度对频率相关函数的影响，同样可以得出当房间宽度B从5 m增加到30 m时，随着频率间隔v′的增加，频率相关函数下降的越来越快，同时带宽也随之减小。

4 结论

    本文推导了室内传播环境下一种宽带移动衰落信道模型。通过假设无限数量的散射体被均匀分布在矩形室二维水平面上，将宽带扩展应用在几何散射体模型上。另外还推导了到达角（AOA）概率分布函数（PDF）、功率延迟分布（PDP）、频率相关函数（FCF）的解析表达式。文中结果分析表明，到达角概率分布函数的大小与基站BS的位置无关。矩形室的长度A和宽度B两者同样对到达角概率分布函数和频率相关函数有影响，如果房间的长度A或宽度B增加，随着频率间隔v′的增加频率相关函数下降的越来越快，同时随着房间长宽的增加，相干带宽减小。

    本文通过运用SOC原理根据参考信道模型推导了一种高效信道模拟器。从频率相关函数、时间相关函数等来看，SOC信道仿真模型与宽带参考模型在一定频率、时间延迟范围内非常匹配。SOC信道仿真模型能够更有效地评估宽带室内无线通信系统的性能，同时减少了实现的开支。

参考文献

[1] XU H，KUKSHYA V，RAPPAPORT T S.Spatial and temporal characteristics of 60-GHz indoor channels[J].Selected Areas in Communications，IEEE Journal on，2002，20(3)：620-630.

[2] ATHANASIADOU G E，NIX A R，MCGEEHAN J P.A microcellular ray-tracing propagation model and evaluation of its narrow-band and wide-band predictions[J].Selected Areas in Communications，IEEE Journal on，2000，18(3)：322-335. 

[3] PATZOLD M，HOGSTAD B O.A wideband space-time MIMO channel simulator based on the geometrical onering model[C].Vehicular Technology Conference，2006.VTC-2006 Fall.2006 IEEE 64th.IEEE，2006：1-6.

[4] 江浩，周杰.室内外非对称信道模型及其MIMO研究[J].安徽大学学报(自然科学版)，2013(5)：51-59.

[5] MA Y，PATZOLD M.Design and simulation of narrowband indoor radio propagation channels under LOS and NLOS propagation conditions[C].Vehicular Technology Conference(VTC 2010-Spring)，2010 IEEE 71st.IEEE，2010：1-7.

[6] PAPOULIS A，PILLAI S U.Probability, random variables,and stochastic processes[M].Tata McGraw-Hill Education，2002.

[7] GUTIERREZ C A，PATZOLD M.The design of sum-of-cisoids Rayleigh fading channel simulators assuming nonisotropic scattering conditions[J].Wireless Communications，IEEE Transactions on，2010，9(4)：1308-1314.

[8] PATZOLD M.Mobile fading channels[M].John Wiley & Sons，Inc，2003.