文献标识码: A
DOI:10.16157/j.issn.0258-7998.2015.09.026
中文引用格式: 张晓蕾,马晓丽. 一种基于云计算的大图高频模式挖掘算法[J].电子技术应用,2015,41(9):95-98.
英文引用格式: Zhang Xiaolei,Ma Xiaoli. A high frequency patterns mining algorithm of big graph based on cloud computing[J].Application of Electronic Technique,2015,41(9):95-98.
0 引言
图挖掘问题[1-3]在移动互联网、大数据处理等领域具有十分重要的应用价值,是目前的研究热点。文献[4]提出了一种基于共生频繁项树和逆矩阵的图挖掘算法。文献[5]中的SpiderMine算法采用概率挖掘理论来寻找前K个最大模式,通过将小规模高频率模式融合为大规模模式,克服了算法瓶颈,效率较高。文献[6]提出了一种自适应云端的大规模导出子图提取算法,以解决资源优化利用与海量图挖掘等问题。文献[7]提出一种图形挖掘系统OPAvion。然而,上述方法均无法进行云环境下大规模图形的高频率模式挖掘。为了解决以上问题,本文针对文献[5]中的SpiderMine算法提出云环境下的新算法c-SpiderMine。c-SpiderMine包括分区、挖掘、融合3个阶段。分区阶段利用最小切割算法将大规模图形数据分为多个子图,使分区/融合成本最小。第2阶段为挖掘阶段,利用SpiderMine进行模式挖掘,利用约简器可有效降低图形同构测试的成本,显著降低大型模式生成时的组合复杂度。更重要的是,本文构建一个全局表格以避免该阶段出现不对称信息,最后一个阶段是模式融合。本文提出一种模式键(Pattern Key,PK)函数来保存模式,以保证所有模式可被成功恢复和融合。
1 问题描述
1.1 图分割
将输入的数据图表示为G,将分割数据集表示为S。图分割问题可定义如下:
定义1:已知图形G=(V,E),切边集合C(Ec),其中Ec将G分为多个分区{S1,S2,…,Sn},且对任意i≠j有Ui Si=V。切边集合Ec为顶点属于不同分区的边集合。
1.2 不对称信息
基于经典的MapReduce[8]模型,本文在分区阶段将图形G分割为多个子图S1,S2,…,Sn。在挖掘阶段,需要挖掘初始时频率较低的图形模式,称为spider,定义2中对此进行描述。
定义2:将半径约束在r范围内的高频率模式称为r-spider。用图形的头部表示每个spider,Spider的半径为其节点的最小偏心率,因此,radius(spider)=min{e(v):v∈V(spider)}。
1.3 模式融合
在融合阶段,将利用挖掘阶段生成的spider生成全局高频率模式。这一问题的简单求解方法是发送spider然后对其融合。然而,如果在一台机器上融合所有图形,则将产生两个问题。首先,约简程序的存储空间无法从所有映射程序中读取所有的高频率子图,因为高频率模式集合的数据规模大于原始的输入图形规模。其次,难以定义合适的融合键值。对键值做普通选择会复制切割节点。然而,选择这些节点作为键值会导致部分大规模模式无法被融合。
2 c-SpiderMine算法
图1给出了本文方法的框架。

2.1 分割阶段
本文采用最小切边算法来进行图分割。最小切边集合概念见定义3。
定义3:已知图形G(V,E),其中V表示顶点结合,E表示边缘集合,G(V,E)的最小切边集合Ec(S,T)可将V分割为S且T=V-S,同时有s∈S,t∈T,且Ec(S,T)=Ec(u,v)的容量最小。
为了将图形G(V,E)分割为k个均匀子图且每个子图均能保留其结构,首先利用最小切边集合Ec将一个图形分割为多个子图,然后,在u和v分别隶属的两个子图中,复制最小切边集合Ec上的所有节点对(u,v)。该阶段算法见算法1。
算法1:分割阶段
要求:图G=(V,E)
k:图形分割数量
输出:Gsub={g1,…,gk},G被分割的子图
1: Gsub←k-Partition(G,k)
2: for 每个gi,gj∈Gsub do
3: Ec←{(vi,vj)|vi∈gi(V),vj∈gj(V)}
//添加gi和gj中的切边集合Ec
4: gi(E)←gi(E)∪Ec
//添加gi的切割节点集合Vc的连通边缘
5: gi(E)←gi(E)∪{(vi,vj)|vi∈Ec|vj∈Ec∧i≠j}
6: 输出所有子图Gsub
2.2 挖掘阶段
在挖掘阶段的第1步,采用文献[9]中提出的模式增长算法实现spider增长,以便在半径约束内挖掘所有的高频率图形模式,它只需一个处理器就可获得所有的初始spider。在该阶段中,首先需要选择一个节点作为初始模式。然后,算法利用与模式相连的边来扩展模式,进而生成新的候选。算法还收集模式嵌入因子。如果嵌入因子数量低于支持阈值,则算法修剪候选。为了实现spider的并行增长,本文采用BSP模型来增长相同深度内不同子图中的spider,即可以在同一超级步骤内生成边缘和节点数量相同的所有高频率spider候选。在挖掘阶段的第2步中,通过构建一个全局表来维护每个spider候选的支持数。在同频率图形模式候选集合增长期间,通过Canonical forms[10]对候选模式进行编码,将每个候选模式的本地支持量发送给全局表。然后,在超级步骤结束后修剪频率较低的候选,并确保所有处理器均增加了候选的可能嵌入因子数。通过这种方法可以保证不会有模式由于信息不对称而被修剪。挖掘阶段的整个步骤见算法2。
算法2:MiningPhase(挖掘阶段)
要求:Gsub:分割后的子图
r:图形半径
最小支持阈值
输出:〈Ec(Gid),S′〉,Gsub中的切边集合和高频率图形模式集合
Map(Key k,Value v)
1: Gid←k//键定义为子图ID
2: Gsub←v//值定义为子图数据
3: 利用标识频率对Gsub中所有节点进行同步和排序
4: for all gi∈Gsub do
5: 修剪低频率标识,重新标识gi的节点
6: 输出〈Gid,Gsub〉
Reduce(Key k,Values v[])
1: Gid←k//键为子图ID
2: Gsub←v//值为子图数据
3: S1←Gsub中所有本地高频率单边图形
4: for 每个s∈S1 do
5: supglobal(s)←CalculateSupport(s)
6: S∈S1;
7: if S≠?覫 do
8: for 每个s∈S do
9: if supglobal(s)<?兹且Radius(s)≠r then
10:S′←S-{s}
11: else
12:S′←GrowPattern{s}
//生成候选图形模式并更新supglobal
13:sync(s,supglobal)//BSP模型同步
14: 输出〈Ec(Gid),S′〉
2.3 融合阶段
融合阶段包括两个MapReduce任务。第1个任务是将不同子图中的spider扩展为更大规模的模式。为了解决融合问题,文中提出一种基于重叠的模式键(Pattern Key,PK)函数。键(key)定义为每个高频率图形模式候选的哈希码,值(value)定义为候选spider每个子图中嵌入因子数的支持数之和。PK函数的作用在于保留初始关系,提供两个子图间的关联。PK函数的定义见定义4。
定义4:已知一个子图g(V,E),其中V表示节点集合,E表示边集,Vc表示复制节点集。将切割节点vc∈Vc的重叠切割节点集定义。
第2个任务称为模式修剪任务,内容是当两个模式同形时修剪掉重复的模式。模式修剪任务之后,可以计算每个模式的支持数。最后,将所有模式发送给模式融合任务。因为本文已经在先前的任务中修剪掉了低频率模式并进行了同构测试,所以通过检查两个模式是否拥有相同的PK来进行模式融合。如果两个模式的PK相同,则通过该相同的spider对其融合。重复这一步骤,直到新生成的模式的直径超出直径界限为止。限于篇幅,融合阶段的详细步骤在此略去。
3 仿真实验
3.1 实验环境
本文在33个虚拟机构成的云计算环境下,将c-SpiderMine部署于HAMA 0.5和Hadoop 1.0.3上,其中一个节点作为主节点,其余节点均作为从属节点。所有实验运行于256 GB内存和1 GB以太网英特尔Xeon服务器平台上。
3.2 与SpiderMine的比较
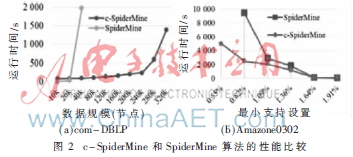
为了证明c-SpiderMine的有效性,选择SpiderMine作为基准算法来比较节点数量不同时的运行时间,最小支持数不同时的运行时间及内存使用情况。从网站上选择两种大型数据集[11]进行测试,如图2(a)所示,当节点规模变大时运行时间上升,在该图中,可以发现当数据规模大于20 000时,SpiderMine难以为图形提供支持,相反,当数据规模增大时,c-SpiderMine的性能较优。图2(b)表明即使最小支持数较低,c-SpiderMine在运行时间方面的性能仍优于SpiderMine。此外,可以发现当最少支持数低于0.82%时,c-SpiderMine优于SpiderMine。总体来说,本文c-SpiderMine方法在处理大规模图形数据时显示出了良好的运行时间性能,降低了内存使用量,且效率高于SpiderMine。
3.3 伸缩性
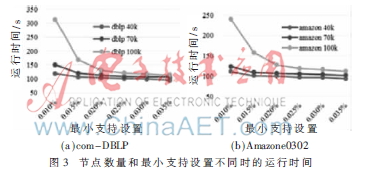
(1)最小支持设置的影响:下面分别在图3(a)和3(b)中给出com-DBLP和Amazone0302的运行时间。两组实验的最小支持设置范围为0.01%-0.035%,节点规模分别为40 000、70 000和100 000。结果表明,当最小支持设置增加时,运行时间下降。这表明,当最小支持设置增加时,生成的模式数量变小,运行时间降低。此外,当N增加时,运行时间同步增加,明显表明有更多的节点生成更多的模式,消耗更多的时间。实验表明,当节点规模和最小支持数增加时,c-SpiderMine在运行时间方面具有良好的伸缩性。
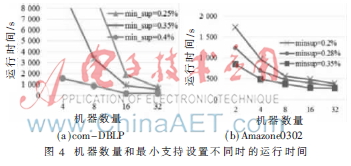
(2)机器数量的影响:本节研究了机器数量不同时的性能。验证c-SpiderMine的性能时,对com-DBLP数据集使用4、8、16和32台机器,最小支持设置为0.25%、0.35%和0.4%,对Amazone0302数据集使用2、4、8、16和32台机器,最小支持设置为0.2%、0.28%和0.35%。在图4(a)和4(b)中,当机器数量上升时运行时间呈指数下降。结果表明,机器数量增加可提高性能和效率,这进一步证明云计算可直接提高大规模图形数据挖掘的伸缩性。
4 结论
本文提出了c-SpiderMine算法,在处理大规模图形数据时有效融合了BSP模型、SpiderMine和云计算。实验结果表明,在不同数据规模和最小支持设置条件下,c-SpiderMine在内存使用和运行时间方面的性能均优于SpiderMine。文中还证明了c-SpiderMine在不同的最小支持设置和机器数量条件下,具有良好的伸缩性。在下一步工作中,可结合更多的真实大型数据集对本文方法展开研究。
参考文献
[1] 孙鹤立,陈强,刘玮,等.利用MapReduce平台实现高效并行的频繁子图挖掘[J].计算机科学与探索,2014,8(7):790-801.
[2] ANCHURI P,ZAKI M J,BARKOL O,et al.Approximate graph mining with label costs[C].Proceedings of the 19th ACM SIGKDD international conference on Knowledge discovery and data mining.ACM,2013:518-526.
[3] KANG U,AKOGLU L,CHAU D H P.Big graph mining:algorithms,anomaly detection,and applications[J].Proceedingsof the ACM ASONAM,2013,13:25-28.
[4] 李涛,肖南峰.基于共生频繁项树和逆矩阵的图挖掘[J].计算机应用研究,2014,31(10):2916-2919.
[5] ZHU F,QU Q,LO D,et al.Mining top-k large structural patterns in a massive network[J].Proceedings of the VLDB Endowment,2011,4(11):807-818.
[6] 郭鑫,董坚峰,周清平.自适应云端的大规模导出子图提取算法[J].计算机科学,2014,41(6):155-160.
[7] AKOGLU L,CHAU D H,KANG U,et al.Opavion:mining and visualization in large graphs[C].Proceedings of the 2012ACM SIGMOD International Conference on Management of Data.ACM,2012:717-720.
[8] SARMA A D,AFRATI F N,SALIHOGLU S,et al.Upper and lower bounds on the cost of a map-reduce computa-tion[C].Proceedings of the VLDB Endowment. VLDB Endowment,2013,6(4):277-288.
[9] BORGELT C,MEINL T,BERTHOLD M.Moss:a program for molecular substructure mining[C].Proceedings of the 1st international workshop on open source data mining:frequentpattern mining implementations.ACM,2005:6-15.
[10] BORGELT C.Canonical forms for frequent graph mining[M].Advances in Data Analysis,Springer Berlin Heidelberg,2007:337-349.
[11] LESKOVEC J.Stanford large network dataset collection[J].URL http://snap.stanford.edu/data/index.html,2011.

