0 引言

　　现代临床医学中，实现病灶轮廓精准地自提取成为当下医务人员关注的焦点之一[1]。Kass[2]等人在1987年提出的Snake模型能够动态拟合目标区域的轮廓，但其同样存在着缺陷[3]：模型初始轮廓曲线的捕获范围小，且无法收敛到模型的凹陷区域。1998年Chenyang等人[4]提出了梯度矢量流模型，克服了Snake模型的缺陷。但是，其捕获范围的增大是以牺牲迭代次数为代价的[5]，这在医学图像集的批量处理过程中是不被允许的。本文针对传统GVF-Snake模型出现的问题，提出了一种优化的分割算法，使初始轮廓线尽可能地设置在模型边缘，最后再利用本文提出的改进G-S模型进行曲线自适应，实现病灶信息的精准提取。

1 基于区域的初始轮廓线

　　利用G-S模型分割图像的关键点之一是初始轮廓线的设定[6]。若初始轮廓线设定在GVF力场作用域外，则收敛时可能出现能量为零的情况；若扩大了GVF力场作用域，则必须增加迭代次数才能使曲线逼近轮廓线。

　　在肝病诊断过程中，实现初始轮廓线的自动设定按目前技术而言是难以完成的。因此，本文将人机交互结合区域算法，半自动地实现腹部CT切片集中肝脏病灶初始轮廓线的设定。算法流程如图1所示。

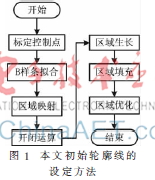
　　肝脏病灶表现为圆状局部暗影,且绝大多数肝脏占位性病变区域较小，在CT平扫时属于低密度，而门静脉和胆管也表现为低密度[7]。这些都为肝脏病灶的提取增加了难度。为了保证病变位置的准确判定，首先利用鼠标手动标定病灶轮廓点，并对拟合后的轮廓线进行逐张映射，最后只需要采取一些简单的步骤对轮廓进行修正。

　　1.1 预处理

　　1.1.1 开闭运算

　　区域内部的细节对基于区域的算法影响较大。所以在修正前需要对区域进行数学形态学中的开闭运算处理以去除噪声、填补缺口[8]。

　　1.1.2 区域生长

　　区域生长是以区域内部某个点作为种子点，并以此为起点搜索出区域内的所有像素。该算法是这样定义边界的[9]：区域边界上像素点的灰度都是某个定值，且区域边界内部均不取这个值，而区域外部的像素点可以取。

　　1.1.3 区域填充

　　用区域生长算法串行构造病灶区域，易于实现，但生长过程中区域内可能还存在着一些孤立点，若直接进行二值化处理会出现许多噪声。这时需要通过区域填充法填补区域内部剩余的孔洞。区域填充结果如图2所示。

　　1.2 区域优化

　　由于相邻切片具有部分差异，经过预处理后的分割区域仍然不能体现当前切片的真实轮廓。其可能存在着弱对象漏分割或对象域溢出的现象[10]。

　　先求出当前分割结果与上一张分割结果的共有区域（如图3（a））的灰度均值α及标准差ｄ，再求出上一张分割结果的特有区域（如图3（b））的灰度均值α0及标准差d0。若|α-α0|<λ，|d-d0|<δ，λ、δ为门限值，则认为这个特有区域为弱对象区域，也属于病灶的一部分。

　　假设弱对象区域（Ω）的灰度为ω，已分割区域（Ω1）的灰度为ω1，背景区域（Ω2）的灰度为ω2，则有ω1<ω<ω2。此时填充对象域，将Ω1的灰度值变为ω2，即令已分割区域变为背景区域的一部分，并让此时的弱对象区域合并入原先的已分割区域。

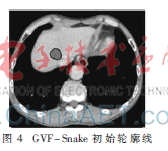
　　类似地，若出现分割溢出的现象，可以通过背景域填充法，将Ω2的灰度值转化为区域的平均灰度值α2，使得背景区域与病灶区域相接，去除了多余的分割区域。得到的初始轮廓如图4所示。

2 改进的G-S模型

　　2.1 基本思想

　　Snake模型可以表示为曲线(s)=(x(s)，y(s))，其中s∈[0，1]。令内力Fint=c1ss+c2ssss，外力Fext=Eext，则Fint+Fext=0时能量最小。

　　GVF利用梯度矢量流场作为外部能量以增加外力的作用范围，即用F(x，y)作为模型中的Fext[11]：

　　Fext=FGVF=F(x，y)=[u(x，y)，v(x，y)](1)

　　2.2 改进模型的提出

　　在患者的一张腹部CT图像中，非目标病灶或是阴影区域是普遍存在的，这些都可能致使拟合的最终结果产生伪边界。而传统的GVF模型无法减少伪边界的影响，尤其当伪边界具有高强度或是在目标区域附近时，影响更为显著[12]。为了突显真实边界，使轮廓线能够更充分地收敛至凹陷区域，利用区域内部信息，假设在CT图I(x，y)中病灶区域为R，轮廓线为Γ(s)，图像大小为a×b，且沿着Γ(s)正方向运动时R总在其左侧。在这里将R的灰度信息SR定义为：

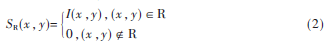
　　则Snake模型的能量函数可以被改写为：

　　其中c3为加权系数，ER表示病灶区域的能量。

　　根据初始轮廓线与病灶区域的位置关系，假定曲线做收缩运动时，则可以得到转换算子H如下：

3 实验与分析

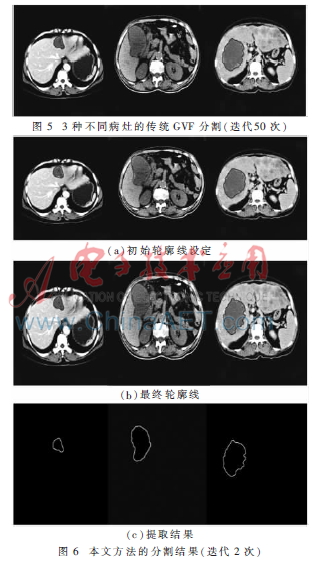
　　为验证算法的可行性与通用性，本文以网站http://www.iiyi.com提供的患者腹部CT图像为实验素材，选取出其中3组具有代表性的切片集，即肝囊性占位、肝肿瘤和肝转移癌，采用Microsoft Visual C++6.0，调用库OpenCV 1.0.0版在PC上实现了上述算法，对肝脏的病灶信息进行了提取。图5采用了传统的GVF算法。图6为利用本文算法进行提取的结果，其中图6（a）为设定的初始轮廓线，经过两次GVF迭代后最终获取结果如图6（b）、图6（c）所示。

　　设Γ1为最终拟合的病灶轮廓，Γ2为真实轮廓，利用拟合指数AOM和距离系数MCD来判定提取的精确度，具体如下：

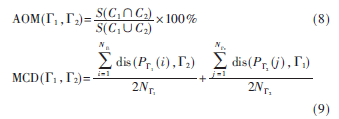
　　其中S表示面积，C1和C2分别为Γ1、Γ2所包围的区域，dis(x，y)为线上的点x与线y之间的垂直距离，N代表对应线上的总点数。AOM反映了曲线间的相似性，而MCD反映了曲线的差异性。编程对实验的3组切片数据进行计算，结果如表1所示。

　　通过对比表1中的数据可以看出，本文提出的算法能够精准地分割出病灶区域，且对于复杂区域的提取有着较大优势。传统的模型进行轮廓线提取时一般需要经过几十次以上的迭代，对于灰度特征较复杂的病灶区域来说容易拟合至伪边界，导致提取结果不准确。本文改进了初始轮廓线的设定方法，半自动地限定了主动轮廓的运动范围，使提取过程更具针对性，迭代时间缩短至5 s左右，大大提高了提取的效率。实验结果表明，在内外力的共同作用下，运动的曲线可以在达到平衡时很好地自适应病灶的真实轮廓。

4 结论

　　本文提供了一种快速有效的提取方法，既保留了G-S模型能够收敛于凹陷区域的优越性，又克服了其因扩大了捕获范围而增大了运算量的缺陷。同时，结合区域信息，本文改进了传统的G-S模型，提高了轮廓提取的精度。该算法适用于CT切片集的批量处理，可实现病灶复杂区域的连续精准分割，为CT图像分割问题提供了新的解决方案。

参考文献

　　[1] 彭微．基于区域的肝脏病灶CT图像分割及实现[J]．信息技术，2011(11)：132-133.

　　[2] LU H Y，YU Y M，BAO S L.Note：on modeling techniquesin active contours[C].Beijing：IEEE，ICSP，2012：956-961.

　　[3] 王雅萍，郭雷．一种基于轮廓自扩展的GVF算法[J]．火力与指挥控制，2009，34(4)：147-149.

　　[4] SONG X D，TANG G A，LI F Y，et al.Extraction of loess shoulder-line based on the parallel GVF snake model in the loess hilly area of China[J].Computers & Geosciences，2013(10)：11-20.

　　[5] 范延滨，刘彩霞，贾世宇，等．GVF Snake模型中初始轮廓线设置算法的研究[J]．中国图象图形学报，2008，13(1)：61-66.

　　[6] DU J H，ZHAO G S，ZHANG H L，et al.A novel method in extracranial removal of brain MR images[J].Procedia Computer Science，2014(3)：1160-1169.

　　[7] 吴锦．CT平扫与多期增强对肝脏实性占位病变检出价值的探讨[D]．长沙：中南大学，2014.

　　[8] 胡涛，吕虹，孙小虎，等．基于水平垂直灰度开运算的车牌字符分割算法[J].电子技术应用，2012，38(10)：11-13．

　　[9] 秦晓薇．区域填充算法的研究[J]．赤峰学院学报(自然科学版)，2011，27(6)：28-30.

　　[10] 王瑞鑫．GVF Snake算法的改进及其在肺癌检测技术中的应用[D]．秦皇岛：燕山大学，2010.

　　[11] LI X G，SHEN L S，LAM K M.An image magification algorithm using the GVF constraint model[J].Journal of Electronics，2008，25(4)：568-571.

　　[12] ZHAO J，ZHANG L，YIN M M.Medical image segmenta-tion based on wavelet analysis and gradient vector flow[J].Journal of Software Engineering and Applications，2014，7(12)：1019-1030.