0 引言

　　在无损探伤过程中，探头处发射的超声波在缺陷中经过发射被超声波探伤仪接收，以确定缺陷的位置和类型。无损探伤具有检测成本低、速度快和现场使用方便等优点，多用于管道、压力容器等圆柱体构件的探伤检测[1]。计算超声学在近些年应用于超声波检测的模拟，从不同尺度上入手，建立不同的超声波模型，来模拟声束在介质中传播时的声场、缺陷与界面处对超声波的作用规律，构建超声波检测计算模型，整合发展超声波检测的技术，促进超声波检测在无损检测中的应用。对于许多复杂情况而言，理论与实验手段难以进行，但可以利用计算机环境进行仿真计算得到数值结果[2]。本文利用MATLAB加载的k-wave工具箱模拟声场传播和建立缺陷重构模型，使得原有声场建模变得简单、快速[3]。

1 超声场仿真原理

　　本文在均匀背景散射媒介中建立声源模型，简化输入参数在提高计算效率的同时，排除非关键因素，从而有效提取出超声场的精确回波模型。

　　1.1 声速与声压的计算

　　由流体介质中的非线性压力与密度关系，可以将状态扩展为泰勒级数中对应的压力项和密度项。假设非线性和压力的变化影响(由于声波吸收)都是二阶。因此，高阶压力项可以被丢弃。考虑到在很小的有限时间步长t=t1-t0内改变流体元素的总压强，泰勒级数展开可写成：

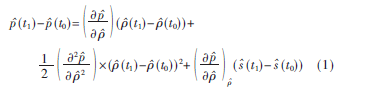
　　式(1)中最后一部分代表一种能量损失也是一种声能吸收。在热粘性介质中，可以结合介质的导热系数和比热容，考虑能量守恒方程[4]，这一点可以表示为一种声学损失模型：

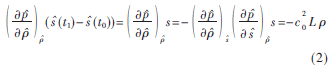
　　L表示声能损失。建立幂律吸收模型，基于分数拉普拉斯算子定义L的表达式为[5]：

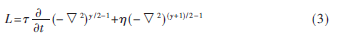
　　τ和η是吸收和色散比例系数[6]。

　　1.2 k-space伪谱法

　　伪谱法求解微分方程主要包含：(1)离散化处理，用一定的方式在整个区域上选取格点构成一个网络。而其它点上的变量值可以用插值的方法得到；(2)选取合适的基函数变量值的情况下构造插值函数，计算格点上变量值的空间导数。伪谱法是全局方法,只能用在空间域。如果所求解的是含时微分方程，一般用简单的有限差分方法来处理时间域的计算[7]。

　　在k-wave中，利用快速傅里叶变换和k-space伪谱法，将守恒方程中的粒子速度和声学密度转换为离散形式，计算每个时间步长内声压场的变化情况，能够高效准确地对超声场进行数值模拟。离散表达式如式(4)～式(7)所示：

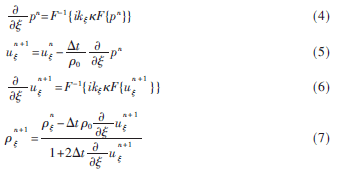
　　声学密度是分布在笛卡儿坐标系中并可以引入各向异性PML应用的值[8]。F和F-1表示空间傅里叶正逆变换，上标n和n+1分别表示函数在当前和下一时间点的值，i为虚数单位，t是时间步长，其中cref为相关声速。

　　式(7)离散方程可利用基于Courant-Friedrichs-Lewy的CFL数值求解时间步长，?驻t=CFL?驻x/cmax。CFL通常取0.3能够平衡准确性和计算效率之间的关系。在每个时间步长内，质量或力源可以通过在计算域内添加适当的网格点值来设置。同样的，模拟的输出可以通过每个时间步长在特定的网格点处的声变量记录[9-10]。

2 声场仿真模型

　　本文设计圆柱体工件超声场模型，并通过传感器接受回波信号。工件的设定如下：实心圆工件半径为2 mm；人造缺陷孔工件中心圆孔工件外半径为2 mm，内半径为1 mm；偏心圆孔工件外半径2 mm，偏心孔中心为半径的中间，半径为0.5 mm，在距离圆柱的中心半径为4.5 mm处设置8个等距离分布的传感器。时间步长为1 μs，由于超声波传播速度很快且工件尺寸很小，本文对超声波在工件内和水中声速的差异不做考虑，超声波传播速度为1 500 m/s。

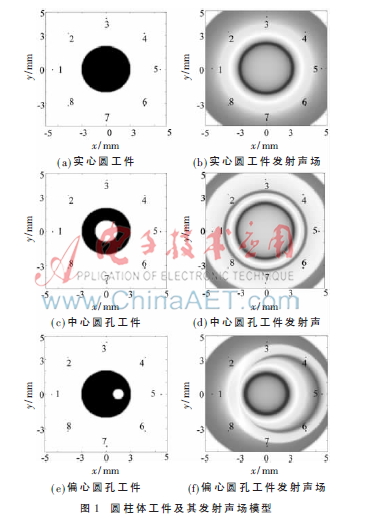
　　根据惠更斯原理，声波遇到障碍物时会以障碍物作为新的声源发射。本文仿真环境以圆柱体工件为新的声源，并设定了8个点传感器的分布位置及其编号，工件将360°接收的单脉冲信号在同一时刻发射出去，如图1所示为不同构件发射声场模型的二维显示图，从中可以很直观地观测到声场传播过程中波形和声压强弱情况，深色到浅色区域即为声压从强到弱体现。

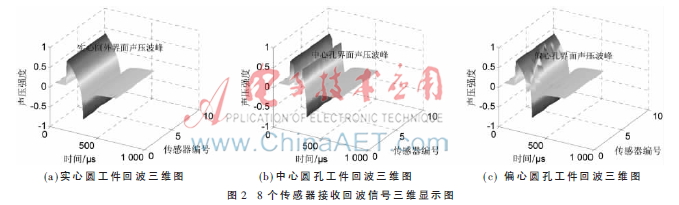
　　图2为8个点传感器探头接收的超声信号三维图，通过与实心圆对比可以明显看出中心圆孔和偏心圆孔发射声场声压的异同之处：(1)由于圆柱位置及外半径设置相同，传感器探头接收信号的起始和终止位置一样；(2)由于中心圆孔的设定位置在传感器探头的正中心，所以8个探头接收到的信号同一时刻达到波峰；(3)根据偏心圆孔设定的位置， 5号最近点传感器会首先接收到回波信号，1号最远点传感器则会最后接收到超声的二次回波信号。

3 逆时反演重构模型

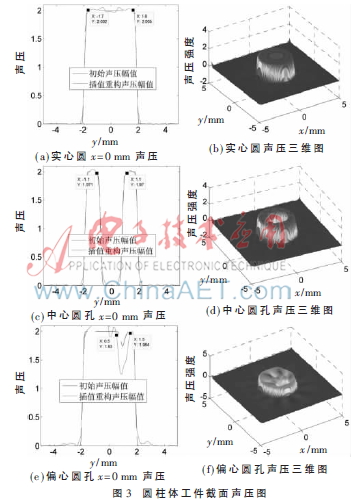
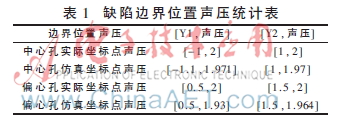
　　利用声学传感器接收到的回波信号逆时反演重构，在圆周上每隔一度设置一个点传感器，使之围绕工件一周，充分接收到不同工件360°的发射声场，利用接收到的发射信号进行逆时反演重构，仿真重构效果如图3(b)、图3(d)～图3(f)所示。如图3(c)，图3(e)所示，声压在人造缺陷孔的边界位置将会有明显变动，缺陷边界处声压坐标值如表1所示。根据测量数据可知，在误差允许范围内缺陷仿真边界坐标点位置与实际缺陷设定尺寸相一致。

4 总结

　　本文利用k-wave工具箱对三种典型的工件模型做了声场仿真研究，设计的仿真平台能够达到实际检测中难以实现的设定，能够实现360°同时刻采集工件的发射信号，减少人为移动工件或探头进行超声探测扫描带来的误差等方面的影响因素，并且能够将声场能量具体化，直观可视化地观测声场在工件中具体传播过程。通过重构结果分析，测得缺陷的位置和尺寸数据与工件的实际设定值相一致，充分说明仿真理论的正确性和仿真结果的准确性。

参考文献

　　[1] 孟凡凯.水下超声波检测声场数值模拟与实验分析[D].哈尔滨：哈尔滨工业大学，2012.

　　[2] COX B T，TREEBY B E.Effect of Sensor Directionality on Photoacoustic Imaging:A Study Using the k-Wave Toolbox.Proc.of SPIE Vol.2010，7564，75640I1-75640I6.

　　[3] TREEBY B E，COX B T.K-Wave：a MATLAB toolbox for simulation and reconstruction of photoacoustic wave-fields[J].J.Biomed.Opt.，2010，15(2)，0213141-02131412.

　　[4] COX B T，KARA S，ARRIDGE S R，et al.K-space prop-agation models for acoustically heterogeneous media：Appli-cation to biomedical photoacoustics[J].J.Acoust.Soc.Am.2007，121(40)：3453-3464.

　　[5] 《超声波探伤》编写组.超声波探伤[M].北京：电力工业出版社，1980.

　　[6] Tabei M，Mast T D，Waag R C.A k-space method for coupled first-order acoustic propagation equations[J].Acoust.Soc.Am，2002，111(1)：53-63.

　　[7] 刘鲁波，陈晓非，王彦宾.切比雪夫伪谱法模拟地震波场[J].西北地震学报，2007（01）：18-25.

　　[8] COX B T，KARA S，ARRIDGE S R，et al.K-space prop-agation models for acoustically heterogeneous media：Appli-cation to biomedical photoacoustics[J].Acoust.Soc.Am，2007，121(6)：3453-3464.

　　[9] Tillett J C，Daoud M I，Lacefield J C，et al.A k-space method for acoustic propagation using coupled first-order equations in three dimensions[J].Acoust.Soc.Am，2009，126(3)：1231-1244.

　　[10] TREEBY B E，JAROS J，RENDELL A P.Modeling nonlinearultrasound propagation inheterogeneo us media with power law absorption using a k-space pseudospectral method[J].Acoust.Soc.Am，2012，131(6)：4324-4336.