0 引言

    LTE系统通常采用的信道估计方法有最小二乘（LS）估计、最小均方误差（MMSE）估计及其改进算法。文献[1，2]分别提出了一种梳状导频MMSE准则的信道估计方法和基于低阶近似以及SVD分解的OLR-MMSE信道估计算法，针对不同的应用场景，对计算复杂度和估计性能折中。文献[3]研究了门限选择算法和即时能量算法，由于这类方法不需要任何的信道统计信息，所以实现简单，但对于时变信道或者终端移动速度较快的环境信道估计性能较差。在工程中，无线信道具有非常复杂的传播路径，会导致多径时延的变化很大。若采用固定的多径时延扩展，则由此引起的相关函数失配会对信道估计性能造成一定的损失^[4]。若能在通信中根据信道条件的变化得到实时的多径时延扩展的估计，并因此调整MMSE信道估计参数，则可获得准最佳的MMSE信道估计性能。基于此，本文提出了一种自适应参数MMSE信道估计系数调整算法，该算法通过对信道均方根时延扩展和信噪比的估计，自适应地调整信道估计参数并生成准最佳的MMSE信道估计系数对LS估计的信道响应进行滤波，较固定系数的MMSE信道估计算法拥有更好的信道估计性能。

1 自适应参数MMSE信道估计系数调整算法

1.1 MMSE信道估计算法

    MMSE信道估计算法原理是求得一个合适的信道冲激响应，使得通过该信道冲激响应计算出来的接收信号与实际信号误差的均方和最小^[5]。

    一般信道估计的模型可以表示为：

    由式(5)可以发现，W与_Rhh和SNR有关，而R_hh又由τ_RMS决定，所以经典的MMSE信道估计受到SNR和τ_RMS的制约，当两个参数和实际信道失配时，性能会急剧恶化。

1.2 自适应参数MMSE信道估计系数调整算法

    从上面MMSE信道估计算法可以看出W由τ_RMS和SNR求出，故τ_RMS和SNR共同决定了MMSE系数。基于此，本文提出的自适应参数MMSE信道估计系数调整算法原理如下：

    由RMS估计模块计算出均方根时延扩展τ_RMS，再由SNR估计模块计算出信噪比估计值SNR，根据SNR和τ_RMS查MMSE系数库得到最匹配参数的MMSE系数，再由式(3)对LS信道估计进行MMSE滤波，得到MMSE信道估计h_mmse。

    自适应参数的信道估计工作过程如图1所示。

1.2.1 RMS估计模块

    首先利用导频，根据式(2)计算LS信道估计，然后计算频域LS信道估计的自相关函数，确定自相关函数3 dB带宽即相关带宽B_c，知道相关带宽B_c后，可以近似认为均方根时延扩展τ_RMS≈1/(5B_c)^[8]。 

1.2.2 SNR估计模块

    计算得到信噪比估计值。

    假设在第m个OFDM符号上的第k个子载波上收到信号表示为：

    由于以下步骤针对每一个子载波k都做处理，所以以下式子省略了下标k。且导频符号位置记为3和10（上行LTE导频符号位置）。

    该方法可以变换成对于每一个符号中的子载波之间做差值的二阶矩处理，从而仅利用一个参考符号就可以估计出噪声方差。

1.2.3 MMSE系数库的建立和系数选取模块

    因为实时在线计算系数需要进行矩阵求逆计算，这样会消耗很长的时间且计算复杂。工程中，为了避免实时矩阵求逆，需要寻求速度和性能的折中，故本算法采用事先建立系数库，然后进行系数选取的方法。

    (1)MMSE系数库的建立

    通过对3GPP信道模型的计算，发现典型的均方根时延扩展值如下：

    ①城市区域：τ_type的值：5e-7、1e-6

    ②农村区域：τ_type的值：1.2e-7

    ③山区区域：τ_type的值：4e-6

    综上所述τ_type的集合为：τ_type=[1.2e-7 5e-7 1e-6 4e-6]这4个值。通过这4个典型值结合信噪比集合ρ_type=[-10 20]生成8个典型MMSE滤波器系数作为MMSE系数库。

    (2)MMSE系数选取

    ①通过RMS估计模块得到τ_RMS，通过SNR估计模块得到SNR。

    ②求系数库中自适应参数的位置参数：

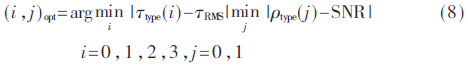
    ③由(i，j)_opt选取对应的MMSE系数。

2 性能仿真

2.1 采用的3GPP典型信道系数

    典型城市区域信道模型，这里叫做Channel Model 0；典型农村区域信道模型，这里叫做Channel Model 1；典型山区区域信道模型，这里叫做Channel Model 2。

    采用MATLAB库函数stdchan()产生上述三种类型的信道衰落系数。

2.2 仿真性能度量准则

    采用归一化最小均方误差（NMSE）作为估计精度的度量准则：

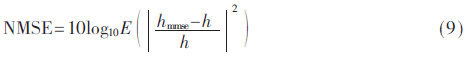
    其中，h_mmse表示MMSE信道估计值，h表示真实的信道频率响应。

    在图 2中遍历不同τ_RMS的情况下，得到NMSE曲线在τ_RMS≈2e-7时达到最小，性能达到最佳，此时的τ_RMS可以认为是真实值τ_actual。而采用自适应参数的信道估计方法计算NMSE，此时τ_RMS≈3e-7，得到的NMSE非常接近真实值τ_actual，之间的差距约为2 dB。若选择的τ_RMS<<τ_actual，NMSE 将急剧恶化，NMSE的最大差距可为16 dB；若选择的τ_RMS>>τ_actual，则NMSE也将恶化，NMSE的最大差距可为10 dB。

    在图3中遍历不同τ_RMS的情况下，得到NMSE曲线在τ_RMS≈3.8e-7达到最小，性能达到最佳，此时的τ_RMS可以认为是真实值τ_actual。采用自适应参数的信道估计方法计算NMSE，此时τ_RMS≈2.8e-7，得到的NMSE非常接近真实值τ_actual，之间的差距约为0.3 dB。

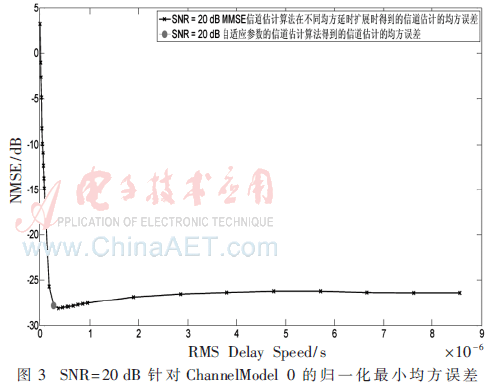
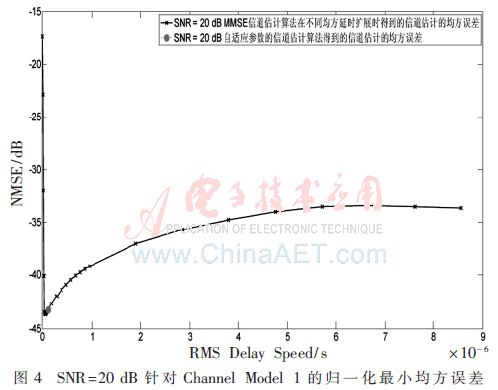
    图4和图5中自适应参数估计的NMSE和真实NMSE差值均仅为0.3 dB。

3 结束语

    本文在已有LTE MMSE信道估计算法的基础上，提出了一种自适应参数的系数调整信道估计算法。仿真结果证实了该算法较固定系数的信道估计算法拥有更好的信道估计性能，采用该方案信道估计的性能比采用固定系数的至少提高3 dB甚至多达10 dB以上。该算法简单可行，适用于工程应用。

参考文献

[1] 石钧，刘泽民.梳状导频的OFDM信道估计改进算法[J].计算机仿真，2013，30(1)：237-240.

[2] 刘玉珍，闫兴玉.MIMO-OFDM系统的低阶信道估计的改进[J].计算机应用与软件，2015(5)：164-167.

[3] 周冰，杨建平.OFDM系统中基于非统计信息的信道估计优化算法研究[J].通信技术，2014(10)：1130-1134.

[4] 徐以涛，王呈贵.OFDM系统基于自适应定阶的MMSE信道估计[J].电子与信息学报，2007，29(1)：117-120.

[5] 张帅，白成林，罗清龙，等.相干光OFDM系统中MMSE信道伏击研究[J].光电子·激光，2013(3)：508-513.

[6] EDFORS O，SANDELL M，Van de Beek J J，et al.Analysis of DFT based channel estimations for OFDM[R].Research Report TULEA，1996：17，Div.of Signal Processing，Lulea University of Technology，1996.

[7] KAY S M.Fundamentals of statistical signal processing：Estimation Theory.Englewood Cliffs，NJ：Prentice-Hall，1993，Ch8.

[8] GOLDSMITH A.Wireless communications[M].Cambridge University Pr.，2005.