0 引言

    遗传算法（Genetic Algorithm，GA）是通过仿生物进化来解决优化问题的一种有效算法^[1]。其中，交叉和变异算子是算法进化的核心，并且对收敛速度和稳定性都有一定的影响。传统的遗传算法采用固定的控制参数，但选择恰当的固定参数是比较困难的。自适应调整遗传算子是解决该问题的有效办法，但同时也遇到了新的问题^[2]，由于在自适应调整的过程中采用的调整方式不同，使得算法在求解时的精确度大小不尽相同。Srinvas等^[3]提出用线性调整（Adaptive GA，AGA）来对交叉率和变异率进行改进，从而提高算法的收敛速度，但在初期会出现停滞现象，导致算法的稳定性和种群的平均适应度值降低。石山等^[4]提出的余弦改进型的自适应遗传算法（CAGA）提高了算法的收敛速度，在算法的中后期促使不理想的个体模式发生变化和保留种群中的优良模式，缺点是当平均适应度和最大适应度差值较大时，个体的交叉率与变异率会出现较大差异，不利于算法演化的进行。赵越等^[5]把交叉率和变异率用曲线进行调整，使收敛速度变快，但是缺乏对个体基因层次上多样性的改进，变异率单调增大的变化趋势导致进化初期产生新个体的能力差和进化末期破坏种群中优良模式的结果。

    文章提出用Logistic型曲线调整交叉算子和变异算子（LOAGA），从进化方向考虑对交叉率和变异率进行自适应调整，比较当代平均适应度值和个体适应度值的大小以及最优个体的适应度值，从而得出该个体的交叉率和变异率。这样既有利于保留较好个体模式，也提高了较差个体的变异能力，使算法尽量避免局部最优解，并且可以克服因早熟产生的不良效果，以及对交叉率和变异率在不同进化阶段的侧重，增加了种群在个体层次上和基因层次上的多样性，从而增强了群体进化的动力。

1 算法分析

1.1 基本遗传算法

    GA是一个反复迭代的过程。其步骤如下：

    (1)确定染色体编码方式和适应度函数及种群初始化；

    (2)评价个体适应度；

    (3)进化开始，执行选择操作和交叉操作及变异操作，产生的个体作为下一代；

    (4)回到(2)，解码新种群并且计算适应度值，如果到达指定精度或设定的进化代数，那么结束，否则执行步骤(3)，继续遗传操作^[6]。

    在用遗传算法解决优化问题时，是根据经验选取固定算子，通过交叉、变异和选择实现父代重组得到子代个体^[7]。而算法实际演化过程中不同阶段对开辟搜索区域的能力和多样性（个体、基因）的要求不同。演化初期应增强种群个体层次上的多样性，对搜索空间有较好的覆盖程度；中期除了考虑搜索空间的覆盖程度外，应加大变异率，增加基因层次上的多样性；收敛性是算法后期需要注意的^[8-9]。GA中固定的交叉率和变异率是根据经验而来，而不是根据实际问题需要自适应调节算子的大小，使得算法在演化过程中的收敛性、稳定性及解的多样性不理想。

    针对固定的遗传算子不利于演化进行的问题，自适应调节遗传算子是解决这个问题的有效办法。

1.2 线性自适应遗传算法

    Srinvas等提出在种群平均适应度值和最大适应度值间进行线性调整算子的大小。如式(1)和式(2)所示。

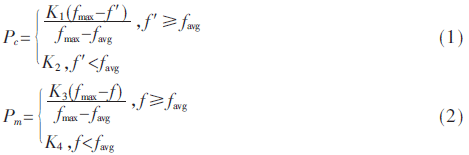
其中，f_max是种群最大适应度值，f_avg是种群平均适应度值，f是变异个体的适应度值，f′是两个交叉个体中的较大适应度值。在上式中，随着f_avg与f_max接近，P_c和P_m就不断变小直至为零。并且，在进化初期，较优个体不发生变化，但这时的优良个体并非全局最优解，会出现局部收敛的可能性。文献[10]中的改进算法（线性自适应，LAGA）可以解决交叉率和变异率为零的问题。式(3)及式(4)是调整公式。

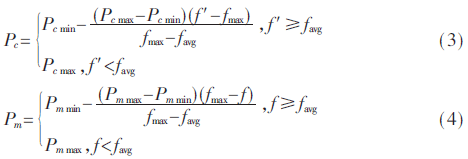
在式(3)、式(4)中，用P_{c max}和P_{c min}表示交叉率最大值和最小值；变异率的最大最小值是P_{m max}和P_{m min}。在求解P_c和P_m时，线性自适应遗传算法是由个体的适应度值在f_avg与f_max间进行线性变换得出的。当大部分个体的适应度值趋近于f_avg时，它们模式相当，成为种群中的主要个体。但是当f_avg和当代种群的f_max接近时，就会出现线性自适应遗传算法的算子调整曲线变得比较陡，P_c和P_m会产生较大差异并且变小，出现演化停滞不前的现象。

1.3 余弦自适应遗传算法

    在文献[4]中，GA的性能与设置交叉率和变异率是否合适有较大的关系，对其设置不当，会影响算法的收敛速度。简单的线性变化得到的交叉率和变异率不能满足算法演化的要求。进而在该文献提出余弦改进型的自适应遗传算法（CAGA），式(5)和式(6)是自适应遗传算子的调节公式：

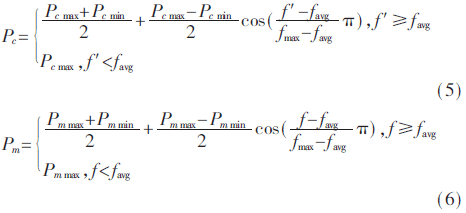
    图1是 CAGA自适应交叉变异调整曲线，在图1中，CAGA比LAGA提升了适应度处于区间[f_avg，(f_avg+f_max)/2]个体的P_c和P_m，促进了f_avg附近不理想的个体模式发生变化。CAGA压低了处于区间[(f_avg+f_max)/2，f_max]个体的P_c和P_m，有利于种群中优良模式的保留。

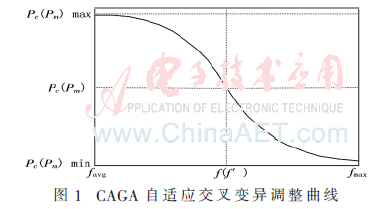
    图2是CAGA与LAGA调整曲线对比图，在CAGA中，P_{c max}和P_{c min}之间的差值很小，且小于等于1，P_{m max}和P_{m min}同样如此。在图2中，|Δf|（f_avg和f_max之间的差值）变化很大，不同优化问题之间也存在区别。当|Δf|很大时，余弦和线性曲线十分接近，说明在一定程度上两者的性能相当，同样有停滞不前的现象。

    在文献[5]中提出的自适应调节公式中，虽然也提到用Logistic曲线对算子进行改进，但在用种群相似度控制变异率时，对进化后期基因层次上的多样性改进不够，变异率偏大会破坏种群中的优良模式。

    分析得到以上算法的主要问题是演化过程中停滞不前，CAGA和LAGA一定程度上性能接近，进化过程中不同阶段侧重不够。因此，从以下几方面解决问题，首先，在f_avg处的调整曲线应该缓慢过渡，目的是较大地提高交叉率和变异率(在适应度接近平均适应度的过程中)。其次，为了当|Δf|较大时，不会出现线性调整的现象，避免停滞不前的现象。再次，使算子的自适应调整满足算法进化前期空间大后期精度高的要求。同时，使接近f_max处的曲线变得更平滑，目的是保留较优个体的模式。

    所以，针对线性自适应调节中出现停滞不前，余弦自适应调节中对算法演化不同阶段侧重不够而使收敛速度慢和解的多样性差的问题，文章用变化更平滑的曲线（Logistics）对交叉和变异算子进行非线性调整，提高算法的收敛速度和解的多样性。

2 LO型曲线的自适应遗传算法改进

2.1 算法改进

    Logistics曲线方程是Verhu推导出来的，在描述某些有界增长现象上有比较好的效果，应用广泛，并且能较好地平衡线性和非线性行为之间的变化。以下是简化处理的方程：

    图3为Logistic函数曲线图，可以看出（a>0），该曲线（比余弦）变化更加细腻。当ax≥9.903 438时，y接近1；当ax＜-9.903 438时，y接近0。式(9)和式(10)是用该曲线求解优化问题的调节公式（交叉率和变异率），其中a=9.903 438。图4和图5分别是LOAGA的自适应调整曲线（交叉率和变异率）。

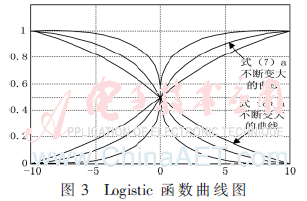
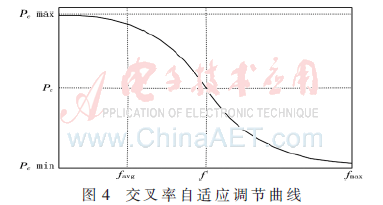
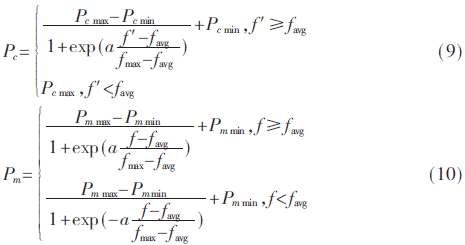
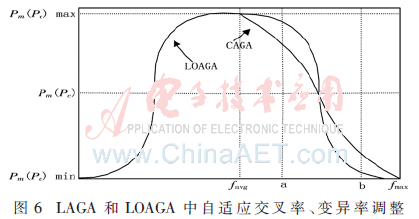
    从改进公式知，当种群开始进化时，LOAGA调整的变异率比余弦函数小，保持种群的优良模式。当f_avg与f_max接近并且大部分个体的适应度值相近时，大多数个体的P_c和P_m变大，且高于余弦函数调整的幅度(图6中a点)。同时，在接近f_max时，低于余弦函数调整的幅度(如图6中b点)，尽可能保留了f_max附近个体的优良模式。在图6的曲线变化趋势上，满足算法进化过程中对不同阶段的侧重（搜索空间上、个体和基因层次上的多样性以及算法后期的收敛方面）。

    在改进后的调整曲线中，无论|Δf|怎么变化都与CAGA和LAGA拉开较大差距，带动了演化的前进，摆脱局部收敛，防止演化停滞不前，如图7所示。

2.2 算法流程

    改进的自适应算法实现步骤如下：

    (1)种群初始化，二进制编码；

    (2)计算适应度值；

    (3)根据f_avg和即将进行交叉及变异操作个体的适应度值，结合自适应调节公式得出P_c和P_m，并进行交叉、变异操作；

    (4)返回(2)，解码并重新进行适应度评价，如果达到指定的要求（精度或进化代数）则结束，否则进行步骤(3)，继续执行操作。流程如图8。

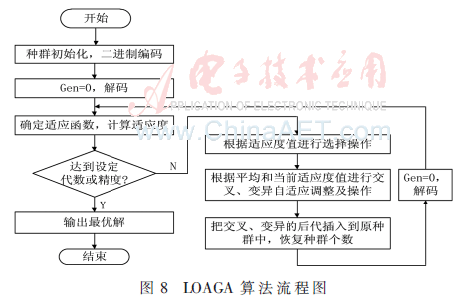
3 实验验证

3.1 算法参数选择

3.1.1 选取函数

    通过对比LOAGA、CAGA、LAGA实验后的数据，来验证改进算法的性能（收敛性和稳定性）。选以下两种函数进行试验。

    理论最小值是-1.031 628，收敛值是-1.031 60。

3.1.2 算法参数

    P_{c max}=0.8，P_{c min}=0.5，P_{m min}=0.05，P_{m max}=0.005，f₁的进化代数是150代，f₂为500代，各运行20次，取均值。

3.2 算法评价

    性能标准的确定：两个函数分别用LOAGA、CAGA、LAGA算法进行测试(运行20次)，算法稳定性用平均收敛次数衡量，收敛速度用平均收敛代数衡量，以平均收敛值接近理想收敛值的程度作为衡量解多样性的标准。

    算法进化的核心是P_c和P_m。整个搜索空间的覆盖程度由Pc控制，用来寻找最优解存在的区域；为保证算法具有全局收敛性，变异算子的作用就是使算法能搜索到解空间中的每一点。文章中在进化的初期提高交叉率（提高搜索空间的覆盖程度），压低变异率（保存原始种群的优良模式）；在中期朝最大适应度进化时拉高交叉（提高提高搜索空间的覆盖程度）和变异算子（使种群有足够基因层次上的多样性）及接近最大适应度时压低两个算子（保存优良模式，收敛），使算法不断进化，尽量避免局部最优解。从表1的数据可以看出，随着种群规模增大，各自的收敛速度变慢（搜索空间变大），LOAGA的收敛速度比CAGA和LAGA的收敛速度慢，但在收敛代数上LOAGA增加的比CAGA和LAGA少（快速找到优良解），不仅在f_avg上高于LAGA，其收敛速度也比前两者快，所以，文章中提出的算法有较快的收敛速度。

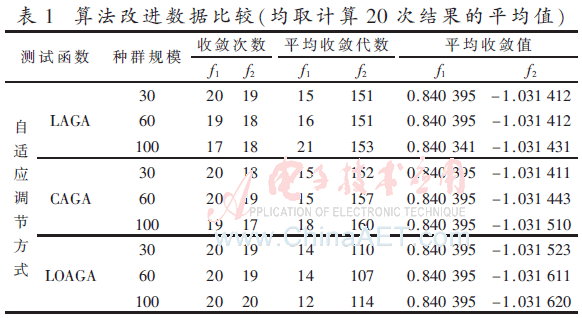
    影响解的多样性有交叉操作产生的个体多样性、变异操作产生的基因多样性及允许父代参与当代竞争的复制方式等因素，文章通过改善交叉率、变异率，增强种群个体和基因层次上的多样性来优化解的多样性，提高解的质量。从表1的数据可以看出随着种群规模的增大，收敛代数增加（搜索空间变大），但LOAGA的收敛值要比CAGA和LAGA的更加接近理想值，（而且增加的收敛代数比CAGA要少，改进后的算法能更快找到优良解），说明提出的算法有更多的优良解。

    从表1知，f₂函数LOAGA的收敛总次数比其他两种要多（快速找到优良解），说明其稳定性好。

4 总结

    文章通过分析交叉率、变异率对遗传算法的影响，指出固定的交叉算子和变异算子及传统改进方法在收敛性和稳定性上的不足。结合Logistics曲线方程，设计了一种新的算法（LOAGA）。它的交叉算子和变异算子受适应度影响，随Logistics曲线自适应调节，相比LAGA和CAGA，无论|Δf|如何变化，通过对新算法的使用，能够较快完成对算子的调整，使算法尽早跳出局部收敛，而且，对交叉率和变异率的自适应调整满足在演化过程中不同阶段对搜索范围和搜索精度的要求。文中提出的算法在收敛速度上和稳定性上有较明显的优势。因此，LOAGA是一种实用的算法，在提高算法的收敛性和增强算法的稳定性及优良解的多样性上是有效果的。

参考文献

[1] Ann Arbor.Adaption in Naural and Artificial Systems[M].University of Michigan Press，1975.

[2] 黄樟灿，李炜.有界区域上多峰函数全局优化问题的改进演化算法[J].武汉大学学报(理学版)，2007，53(1)：55-58.

[3] SRINVAS M，PATNAIK L M.Adaptive probabilities of crossover and，mutation in genetic algorithms[C].In：IEEE Trans on Systems，Man and Cybernetics，1994，24(4).

[4] 石山.基于自适应遗传算法的无刷直流电机的优化设计[J].西安交通大学学报，2002，36(12)：1215-1218.

[5] 赵越，徐鑫.自适应记忆遗传算法研究[J].计算机技术与发展，2014，24（2）：63-66.

[6] 王凌.智能优化算法及其应用[M].北京：清华大学出版社，2000：36-50.

[7] 李书全.遗传算法中的交叉算子的述评[J].计算机工程与应用，2012，48（1）：36-39.

[8] 刘胜.遗传交叉和变异对种群多样性的影响[J].控制与决策，2009，24(10)：1535-1539.

[9] 雷秀娟.群智能优化算法及其应用[M].北京：科学出版社，2012：70-74.

[10] 王小平，曹立明.遗传算法:理论、应用与软件实现[M].西安：西安交通大学出版社，002.