电荷泵锁相环的相位噪声研究-AET-电子技术应用

电荷泵锁相环的相位噪声研究

2016年电子技术应用第1期

童姣叶，李荣宽，何国军

电子科技大学电子工程学院，四川成都611730

摘要： 传统的计算锁相环相位噪声方法没有考虑热噪声、闪烁噪声及基准噪声等影响因素，且不能较好地对应于实际电路。为了更好地解决这个问题，提出了一种简单的方法先分别计算各影响因素引起的相位噪声，然后获得比较实用的锁相环电路的总相位噪声。该方法使用特殊的叠加理论，统一各影响因素在一个实际的锁相环电路中的相位噪声传递函数，从而得到锁相环的总相位噪声。为了验证提出的计算公式的有效性，用标准的CMOS 0.25 μm工艺设计了输出时钟为48 MHz的电荷泵锁相环。仿真结果表明，实现了带内相位噪声低于-88.6 dBc/Hz，带外相位噪声为-108.4 dBc/Hz@1 MHz。这些电路仿真结果与理论计算结果基本一致，它们的绝对误差低于2.54 dBc/Hz。

关键词： 电荷泵锁相环传递函数相位噪声

中图分类号： TN432
文献标识码： A
DOI：10.16157/j.issn.0258-7998.2016.01.006
中文引用格式： 童姣叶，李荣宽，何国军. 电荷泵锁相环的相位噪声研究[J].电子技术应用，2016，42(1)：28-30.
英文引用格式： Tong Jiaoye，Li Rongkuan，He Guojun. Study on phase noise of charge-pump phase-locked loops[J].Application of Electronic Technique，2016，42(1)：28-30.

Study on phase noise of charge-pump phase-locked loops

Tong Jiaoye，Li Rongkuan，He Guojun

School of Electronic Engineering，University of Electronic Science and Technology of China，Chengdu 611730，China

Abstract： Conventional methods of calculating the phase noise usually can′t correspond well with the actual practical circuit without taking into account of thermal noise, flicker noise, shot noise, substrate noise, etc. In order to address the problem, a simple unified method was proposed to calculate the phase noise caused by the affecting factors respectively and then obtain the final total phase noise of an actual practical PLL circuit. The method adopted a special superposition theory to unify all the phase noise transfer functions of the affecting factors in a practical PLL circuit. The unification of the transfer functions enables the total phase noise to be obtained by simple calculation. To verify the effectiveness of the derived formula, an output clock of 48 MHz charge-pump PLL is implemented using a standard 0.25 μm CMOS technology. The simulation results show that the in-band phase noise of -88.6 dBc/Hz and the out-of-band phase noise of -108.4 dBc/Hz at 1 MHz offset are achieved. These circuit simulation results were correlated very well with the theoretical calculation results with an absolute error of less than 2.54 dBc/Hz.

Key words : charge pump phase-locked loop；transfer functions；phase noise

0 引言

随着集成电路技术的迅猛发展，电荷泵锁相环(CP-PLL)由于具有易于集成、低功耗、低抖动等优点，被广泛应用于通信系统、无线电系统、自动控制的时钟数据恢复、频率合成、时钟同步等领域。它的噪声源主要分为两类：(1)参考源的相位噪声；(2)锁相环各个模块的内部噪声。然而，如果不能对电荷泵锁相环的输出信号的相位噪声进行计算，必须等芯片流片后用昂贵的频谱仪来测量。为较大程度上节约设计成本，有必要对电荷泵锁相环的相位噪声研究，预估相位噪声是否达到设计指标。

国内外已发表大量关于锁相环的相位噪声分析文献。文献[1-3]虽然是对锁相环系统的相位噪声进行分析，但仅仅给出压控振荡器的相位噪声计算公式；文献[4]只是简要介绍了锁相环系统相位噪声的分析方法，并没有进行更深入的研究。本文将详细分析并计算电荷泵锁相环系统的相位噪声。

1 锁相环系统的相位噪声

锁相环系统中各个模块都会引入噪声到环路中，但可以利用传递函数来分析各噪声源在系统中的特性。

1.1 锁相环系统的噪声源模型

鉴频鉴相器、电荷泵和环路滤波器每个模块PSS收敛困难^[5]，因此本文将这三个模块作为整体来进行分析。带有噪声源的锁相环线性模型，如图1所示。

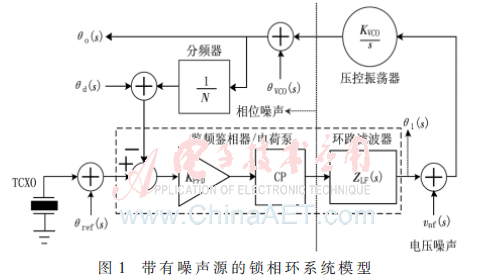
由图1可以得到噪声方程：

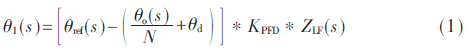
由信号系统理论可得：式(3)、式(6)相同为低通函数；式(4)为带通函数；式(5)为高通函数，并且幅度为1。

1.2 锁相环相位噪声的计算

本文采用的是二阶无源环路滤波器，如图2所示。

则：

上式中I_p为电荷泵电流，K_VCO为振荡器的灵敏度。

因此，由多个噪声源引起的噪声叠加原理^[9]可得：

则可以得到锁相环的总相位噪声计算公式：

由式(10)~式(14)可以计算出电荷泵锁相环系统的相位噪声。

锁相环系统的相位噪声环路带宽内主要由参考源相位噪声决定，环路带宽外主要由压控振荡器的相位噪声决定^[4]。由文献[6-8]可以得到压控振荡器的计算公式：

2 仿真结果

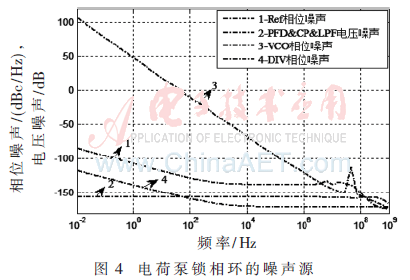
本文的电荷泵锁相环设计参数：f_REF=6 MHz，I_p=20 mA，C₁=6.2 pF，C₂=55.8 pF，K_VCO=10.1 MHz/V，f₀=48 MHz，N=8。图3是电荷泵锁相环各个噪声源的传递函数，图中：1为θ_ref(s)和θ_d(s)的传递函数，2为鉴频鉴相器、电荷泵和环路滤波器噪声v_nf(s)的传递函数，3为θ_VCO(s)的传递函数。从图3中可以看出1为低通函数，2为带通函数，3为高通函数，f_c为带宽。图4是电荷泵锁相环的各个噪声源，图中：1为参考源噪声源θ_ref，2为鉴频鉴相器、电荷泵和环路滤波器噪声源v_nf，3为压控振荡器噪声源θ_VCO，4为分频器噪声源θ_d。电荷泵锁相环的相位噪声主要由参考源相位噪声和压控振荡器的相位噪声决定。

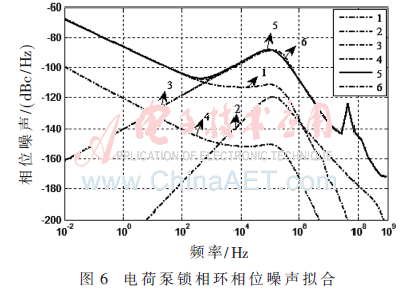
用Cadence软件对整个锁相环系统进行Spectre仿真，得到的相位噪声如图5所示。在Matlab中的理论计算曲线如图6所示，曲线1是参考源的的相位噪声通过锁相环系统环路后的相位噪声；曲线2是电压噪声通过系统环路的相位噪声；曲线3是VCO的相位噪声通过锁相环系统环路后的相位噪声；曲线4是分频器的相位噪声通过系统环路后的相位噪声；曲线5是整个锁相环系统环路总的拟合相位噪声；曲线6是系统环路通过Spectre仿真得到的相位噪声。将此Spectre仿真的总相位噪声导入Maltab中进行比较，以验证计算公式的正确。由式(10)～式(13)得出的各个噪声源的噪声经过环路后的相位噪声，再由式(14)计算得出总的相位噪声，并将Spectre仿真得到的CP-PLL总相位噪声导入其中进行对比，如图6所示。在图中，曲线1是参考源的相位噪声通过CP-PLL系统环路的相位噪声；曲线2是PFD&CP&LPF的电压噪声通过CP-PLL系统环路的相位噪声；曲线3是VCO的相位噪声通过CP-PLL系统环路的相位噪声；曲线4是分频器的相位噪声通过CP-PLL系统环路的相位噪声；曲线5是CP-PLL系统环路的拟合相位噪声；曲线6是CP-PLL系统环路的Spectre相位噪声。由Matlab拟合出的总相位噪声曲线与Spectre仿真得到的总相位噪声基本吻合，最大误差不超过2.54 dBc/Hz。因此，可以由本文的模型和计算方法进行相位噪声的优化研究。

3 结论

本文详细推导了四级差分环形振荡器的相位噪声计算公式，给出了差分环形振荡器延迟单元的电流模噪声模型。基于此模型得到的相位噪声计算公式，更准确地预估环形振荡器的相位噪声。

在CMOS 0.25 μm工艺下，设计了整数型48 MHz的锁相环系统。通过Matlab进行设计和优化系统的参数，建立了各噪声源的仿真电路模型，用Spectre仿真得到各噪声源的相位噪声 (电压噪声) 。同时，比较和分析了Matlab模拟的相位噪声与Spectre仿真得到的锁相环总的相位噪声，并研究了各噪声源对系统相位噪声的影响，实现了带内相位噪声低于-88.6 dBc/Hz，带外相位噪声为-108.4 dBc/Hz@1MHz。这些电路仿真结果与理论计算结果基本一致，它们的绝对误差低于2.54 dBc/Hz。

参考文献

[1] 毕胜兰，戴宇杰，张小兴.电荷泵锁相环系统相位噪声分析[J]．南开大学学报，2008，41(3)：101-104．

[2] 孙添平.电荷泵锁相环的设计及其相位噪声优化[D]．武汉：华中科技大学，2007．

[3] 赵春．基于噪声分析的电荷泵锁相环设计[D]．成都：电子科技大学，2002．

[4] Ali Hajimiri．Noise in Phase-Locked Loops[C]．Mixed-Signal Design，2001，SSMSD.2001 Southwest Symposium on，2001：1-6．

[5] 张涛．锁相环频率合成器建模、设计与实现[D]．武汉：华中科技大学，2006．

[6] Ali Hajimiri，LEE T H．A general theory of phase noise in electrical oscillators[J]．Solid-Stote Circuits，IEEE Journal of，1998，33(2)：179-194．

[7] Hajimiri A，LIMOTYRAKIS S，LEE T H．Jitter and phase noise in ring oscillators[J]．Solid-Stote Circuits，IEEE Journal of，1999，34(6)：790-804．

[8] Ali Hajimiri．Jitter and Phase Noise in Electrical Oscillators[D]．Stanford：electrical engineering from Stanford University，1998．

[9] 李炜．锁相环电路的设计及相位噪声分析[D]．天津：天津大学，2005．

[10] 严杰锋．电荷泵锁相环的模型研究和电路设计[D]．上海：复旦大学，2006．

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容