摘 要: 为提高噪声污染信号的检测速度,研究了一种融合累加平均与小波变换的方法进行信号降噪处理,并测试验证了其有效性。测试结果表明,融合数字累加平均和小波变换的去噪方案在处理速度和降噪效果方面远优于单独累加平均或单独小波变换。对被测信号10 000次累加平均再小波降噪获得的降噪效果与30 000次累加平均相同,但耗时仅为后者的36%,大大提高了信号检测速度。分析比较发现,对带噪信号先累加平均再小波变换方案的去噪效果优于先小波变换再累加平均。
关键词: 信号处理;降噪;累加平均;小波变换
0 引言
基于光时域反射的分布式布里渊光纤传感可以长距离感知整条光纤链路上被测物理参量(例如:温度场、应力/应变等)的空间分布和随时间连续变化信息,在重要军民大型基础设施(如电网、油气管道、煤矿、隧道等)的安全监测领域有广泛的应用前景与市场空间,近年得到极大关注和研究[1-2]。布里渊传感系统通过检测背向散射信号的频移和强度实现信息解。通常背向布里渊散射信号包含大量噪声,其待测有用信号非常微弱。因此,降低噪声提高背向散射信号信噪比和缩短测量时间是布里渊光纤传感系统研究的关键内容之一。
传统的降噪方法基于单纯的累加平均或者单纯的小波阈值降噪。累加平均算法需要对信号进行大量的累加平均以提高信号信噪比,因而导致布里渊传感系统完成一次测量极为耗时,大大降低了系统测量的实时性。小波阈值法能对带噪信号进行包络检测,使去噪后的信号是原始信号的近似最优估计,但是在噪声类型及强度未知的情况下不同阈值的选择对去噪效果影响极大[3]。因此,小波阈值法通常与其他方法结合以达到更优的降噪效果。
本文融合累加平均与小波阈值法在信号降噪中各自优势,采取两种方法相结合对噪声信号进行降噪处理。实验测试结果表明,对待测信号先进行一定次数累加平均,然后再进行小波变换降噪可以获得更好的效果。
1 信号处理原理
1.1 数字累加平均理论
数字累加平均将一次测量的N个数据依次存储到内存单元中,将下一次测量的N个数据与内存对应单元的数据相加再放回原内存单元依次循环K次,然后对各单元求其平均[4]。被测量信号中夹杂的噪声一般为高斯白噪声,其期望值为零,因此K次累加平均后改善的信噪比:

其中,SNR0为经过累加平均处理后输出信号的信噪比,SNRi为未做处理的信号信噪比。M次不同时刻采样的累加平均可以使信噪比改善K倍。累加次数越多,测试时间越长,系统实时性越差[5-7]。
1.2 小波阈值选取原理
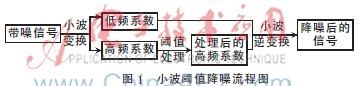
小波降噪法将带噪信号经过预处理,利用小波变换把信号分解到各尺度中,在每一尺度下把属于噪声的小波系数滤除掉,保留并增强属于信号的小波系数,最后再经过小波逆变换恢复信号[8-10]。对一种固定的小波函数,选用的阈值不同降噪效果也不同。针对布里渊散射信号特点,阈值法可采取以下三种形式。
(1)最小极大方差阈值(minimaxi threshold):属于一种固定的阈值形式,使得所选的阈值产生最小的极大方差t:

其中N为小波系数长度。
(2)固定阈值(sqtwolog threshold):由最小极大方差的阈值t再乘以一个系数(logN)得到。
(3)选择启发式阈值(heursure threshold):固定阈值和软阈值的综合,根据信号信噪比大小利用启发函数自动在固定阈值和软阈值中选取一个作为去噪阈值。不同信噪比条件下这两个阈值去噪效果不同。小波阈值法降噪流程如图1所示。
2 实验测试与算法设计
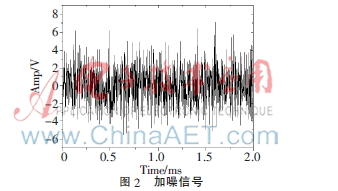
根据上述数字累加平均和小波阈值原理,分别测试了基于数字累加平均、小波变换、先累加平均再小波变换和先小波变换再累加平均等四种方案对噪声信号的降噪性能。其中,以频率为1.5 kHz、幅度为200 mV的方波与幅度为2 V的高斯白噪声相累加模拟布里渊传感系统的布里渊探测信号,如图2所示。信号采集卡与实际布里渊传感系统所用一致(型号为NI-PCI-5112),其最高采样频率为100 MHz,精度为8位。

信号降噪算法流程如图3所示。将采集卡采到的数据送入计算机,分别进行如下四种方案的测试与分析。(1)用单独累加平均的算法对信号进行处理:在虚拟平台上对采集的周期信号分别进行不同次数的加法运算,之后将相对应的加法运算结果进行平均处理;(2)用小波阈值算法对信号进行处理:选用分解级数为5级的“sym8”小波,其阈值采取最小极大方差阈值、固定阈值和启发式阈值三种;(3)先累加平均再小波阈值算法处理:不同累加平均次数后再分别采用上述三种不同的阈值对信号进行处理;(4)先小波阈值处理再累加平均运算:不同小波阈值处理后再进行不同的次数累加平均。上述方法具体信号降噪效果将在下面分别进行分析讨论。
3 实验结果及分析

首先,根据图3所示的算法,分别对上述四种方案进行验证及分析。图4为累加次数分别为300次、1 000次和10 000次处理后的信号,它们所用的测试时间分别为 0.12 s、0.4 s和2 s。此结果表明,随着累加次数的增加高斯白噪声越来越小,但处理时间越来越长。

其次,对被测信号分别进行基于最小极大方差阈值、固定阈值和启发式阈值的小波降噪,测试结果如图5所示。由图可知,最小极大方差阈值(图5(a))和启发式阈值(图5(c))的选取规则较为保守,导致其降噪效果不理想。经过固定阈值处理后的信号幅度更接近原始信号(-0.2 V~0.2 V)(图5(b)),有效去除了随机噪声。由此可见,针对本次实验固定阈值法是最佳选择。从降噪处理所需时间而言,任一小波降噪法处理时间约为 0.1 Vs,仅与不到300次累加平均时间相同。
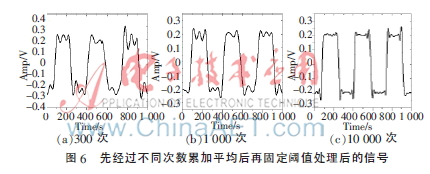
由图4、图5可知,单独基于累加平均和小波变换法降噪存在处理时间长和降噪效果不理想等不足。图6为融合两种方法的信号去噪处理结果:先进行一定次数累加平均再小波变换。其中,对被测信号分别进行300次、1 000次和10 000次累加平均、再做固定阈值算法处理,测试时间分别为0.2 s、0.5 s和2.15 s,累加平均耗时在总耗时中占主导地位。基于其余两种阈值法,去噪效果基本相同。若仅采取累加平均法降噪达到图6(c)所示的降噪效果,则需约30 000次的累加平均,其处理用时高达6 s。因此,融合累加平均和小波变换技术的信号降噪方案大大降低信号处理时间,提高了噪声信号检测速度。
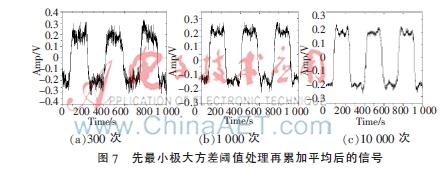
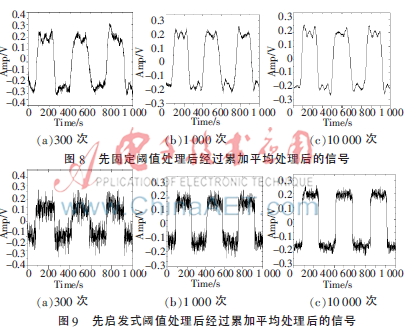
最后,将被测信号先进行小波变换降噪、再进行不同次数的累加平均。图7~图9所用的阈值法分别为最小极大方差阈值、固定阈值和启发式阈值。结果表明,由于被测信号的噪声功率比较大,经过三种不同的阈值处理后,固定阈值处理的降噪效果最好,最小极大方差阈值处理次之。由于启发式阈值法选取规则较为保守(阈值较小,导致只有部分系数置零),所以降噪效果不明显。与图6所示去噪效果相比较可知,在降噪处理耗时基本相同的情况下,第四种方案(即先小波变换再累加平均)要逊于第三种方案(即先累加平均再小波变换)。
综合以上四种方案可得出:(1)小波阈值处理用时最少,但降噪效果差。(2)累加平均算法的降噪效果要明显优于小波阈值处理,并且随着累加次数的增加,降噪效果会越来越好,但运行时间会越来越长,远远不能满足本研究快速处理的要求。(3)累加平均算法与小波阈值处理相结合,降噪效果明显优于单独的数字平均滤波和小波变换方法。与单独累加平均降噪相比较,在相同的降噪效果基础上,该方案有效减少数字平均滤波的累加次数,极大提高了系统噪声信号的检测速度。10 000次累加平均后融合小波降噪获得的信号与30 000次累加平均滤波效果一致,但其耗时(2.15 s)远小于单独累加平均(6 s)。通过比较分析被测信号经过小波阈值处理和累加平均算法的先后顺序可知,被测信号先经过累加平均算法再由小波阈值处理的方法降噪效果最佳。
4 结论
为提高布里渊传感系统中微弱的布里渊探测信号检测速度,测试了四种不同方案的噪声信号降噪效果:累加平均、小波变换、先累加平均再小波变换和先小波变换再累加平均。其中,小波变换采用三种不同的阈值选择原理:最小极大方差阈值、固定阈值和选择启发式阈值。测试结果表明,融合数字累加平均和小波变换的信号降噪效果最佳,处理速度大大提高。10 000次累加平均结合小波降噪方案所获得的信号降噪效果与30 000次累加平均滤波相同,但耗时仅为后者的36%。此外,对带噪信号先累加平均再小波降噪方案的去噪效果优于先小波变换再累加平均。此方法能够有效应用于信号降噪系统处理,可提高光纤传感系统的布里渊探测信号检测速度。
参考文献
[1] BAO X,CHEN L. Recent progress in Brillouin scattering based fiber sensors[J]. Sensors,2011,11(4):4152-4187.
[2] 赵晓东,路元刚,胡君辉,等.波长扫描型布里渊光时域反射仪[J].中国激光,2012,39(8):1-5.
[3] 宋牟平,陈翔.基于实时小波变换信号处理的相干检测布里渊光时域反射计[J].光学学报,2009,29(10): 2818-2821.
[4] FARAHANI M A, WYLIE M T V, CASTILLO-GUERRA E, et al. Reduction in the number of averages required in BOTDA sensors using wavelet denoising techniques[J]. Journal of Lightwave Technology, 2012,30(8):1134-1142.
[5] 李星容,李永倩,张硕.同步叠加平均算法抑制噪声的Labview实现[J].华北电力大学学报,2009,36(4):74-76.
[6] 周倩婷,危峻,徐志鹏.噪声特性对多次采集累加平均技术的影响[J].红外与激光工程,2010,39(5):959-962.
[7] 杨莺,韦育森.提取周期微弱信号的几种软件实现方法[J].测控技术,2008,27(9):22-24.
[8] 张弦,王宏力.进化小波消噪方法及其在滚动轴承故障诊断中的应用[J].机械工程学报,2010,46(15):76-81.
[9] 田玉静,左红伟.小波消噪阈值算法优化[J].声学技术, 2009,28(4):503-506.
[10] 宋牟平,赵斌.希尔伯特变换处理的布里渊散DOFS 的研究[J].光子学报,2005,34(9):1328-1331.

