0 引言

    随着无线网络飞速发展和频谱资源需求剧增，以及无线环境逐步变复杂，使得无线网络系统中的非授权用户想要获得完整的网络环境的参数信息变得愈加困难。因此，对于非完全信息以致未知环境无线网络中的资源分配问题的研究已经成为解决当前网络困境的主要研究方向之一。目前主要应用于未知网络环境下资源分配的理论是部分可观测马尔科夫(Partially Observable Markov Decision Process，POMDP)以及隐马尔科夫模型(Hidden Markov Model，HMM)。文献[1]中将网络环境搭建为未知环境情形，首先通过最大似然算法实现网络中信道使用情形的预测，然后借助POMDP模型实现了网络系统中多信道接入问题。文献[2]为基于未知信息环境认知网络中频谱分配问题，使用Q学习算法机会式频谱接入的研究。文献[5]将POMDP模型与Q学习算法相结合构建了分布式认知网络中的MAC协议，使网络系统中的信道资源得以合理、有效的利用。

    现今基于RMAB或者MAB模型的无线资源分配方法存在两方面局限性：一是对于复杂型网络系统研究较少，尤其是信道模型大多只采用简单的0-1模型进行研究；二是对于存在条件限制的MAB模型研究较少。因此，本文采用了不分时隙的ON-OFF信道模型，并考虑了系统内的干扰限制以及认知用户的感知误差等因素，然后借助Q学习算法实现Gittins索引值算法的求解。最后，通过仿真实验验证了提出的信道选择机制的合理性以及优越性。

1 系统模型

1.1 信道模型

    假设由N个独立的认知用户组成一个认知无线网络，且每个用户均不知其他用户的存在。在此网络中所有的用户共用M个信道，并且在无线网络环境中，由于衰落、干扰以及用户地理位置的差异导致不同信道对同一用户的质量不相同。信道的质量矩阵表示为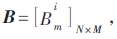用户集合N={1，…，N}，信道集合表示为M={1，…，M}，且1≤M≤N。信道的ON状态和OFF状态交替出现，并且分别服从均值为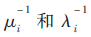的指数分布，信道间相互独立，主用户占用信道的平均概率则可以表示为：P₀=μ_i/(λ_i+μ_i)，信道空闲的平均概率则为：P₁=λ_i/(λ_i+μ_i)。

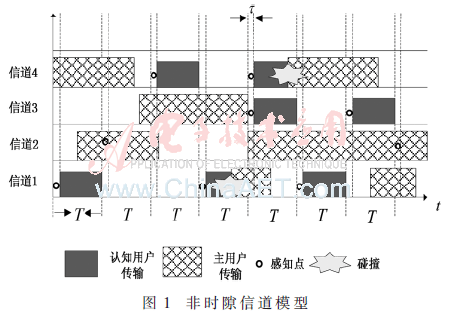
    信道模型和感知模型如图1所示，设时隙长度为T，感知模块的时间为τ。为方便展示，图中只描述了一个认知用户的感知情形。

    假设认知用户采用能量感知形式进行信道可用性感知。认知用户感知阶段接收到的信道表示为：

    H₁：y(t)=u(t)

    H₀：y(t)=u(t)+s(t)

    H₀表示为主用户占用信道，H₁表示信道空闲状态，u(t)和s(t)分别为噪声与主用户信号的抽样值，并且彼此相互独立。能量检测表示为：

1.2 效用函数

    系统的值函数表示为：

    其中ω_n，i(t)表示当前信道空闲的概率，B_n，i表示用户n使用信道i时的信道带宽，(T-τ)表示信道空闲时认知用户传输的时间长度，ω_n，i(t)exp(-λ_iT)表示信道空闲且时间持续为 T的概率。在此需要针对不同的用户找到相应的最优策略ρ^*：

1.3 干扰概率

    因为认知用户对网络环境中主用户的行为是未知的，且信道状态在感知阶段不发生变化，只在认知用户传输阶段改变。则有感知阶段信道状态为0，且持续时间T的概率为：

2 信道参数学习算法

    图2所描述的是认知用户节点的不规则采样图。

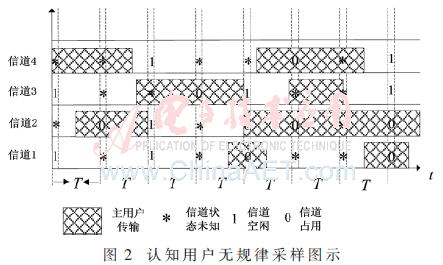
    将连续时间马尔科夫链的参数估计问题转换为离散时间的马尔科夫参数估计问题，然后采用最大期望算法(Expectation-Maximization Algorithm，EMA)实现参数估计。

其中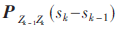表示在采样时间间隔s_k-s_k-1内采样值由z_k-1无间隔转变为z_k的概率。假设S表示在采样空间中所有采样间隔的总个数，O_ijt表示经过t个时间间隔后所观测的数据中从状态i转变为j的次数，(P^t)_ij表示矩阵(P^t)中第i行第j列元素。所以估计矩阵的近似表示也可以写成：

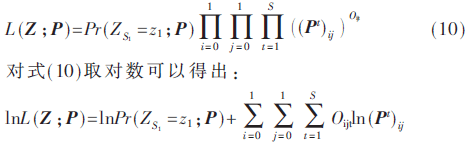
    由对数公式可知，如果S=1则转移矩阵估计可以直接由数学公式求出，但是在本系统中使用的S远远大于1，所以提出使用EMA算法实现转移矩阵的估计。

    假定第l次的E步操作中获得P的对数似然估计值表示为P^(l)，此时的采样值(非完全数据)仍表示为Z，Y为未完全观测值Z构建的一个完全的数据阵，则在l+1次的E步操作中的计算表示为：

    综上可知，通过已知的未完全观测数据以及设定初始的转移矩阵P⁽⁰⁾、算法收敛条件ε，然后经过式(13)和式(14)不断迭代直至最终收敛，可得出转移矩阵的估计值P。

3 基于Q学习算法Gittins索引值计算

    具体的Q学习算法的操作步骤如下：

    (1)初始化用户的Q_n=(s_i，t，a_n，i，t)=0；

(2)每个用户在时隙感知阶段以概率P_t(n，i)随机地选择所要感知的信道，其中：

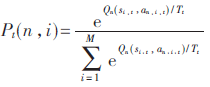
其中T表示波尔兹曼干扰温度系数。

    根据文献[8]提出的结论，可以得出此过程中状态x的Gittins索引值为：

    (3)用户n以P_t(n，i)的概率的大小排序各个信道并从中选择一个或者多个信道进行感知，根据感知结果用户制定相应的行为策略去更新不同行为下的Q_n(s_i，t，a_n，i，t)，计算信道在不同行为下的Gittins索引值，并选择对其中索引值最大的一个或者多个信道进行接入、传输数据，然后根据立即回报值，更新各自的Q值：

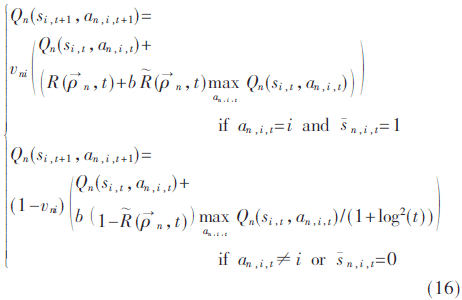
    其中，v_ni表示为用户n对信道i的学习因子，其数学公式表示为：

    ω_n，i，t表示为用户n对信道i空闲的信任概率值，其更新公式：

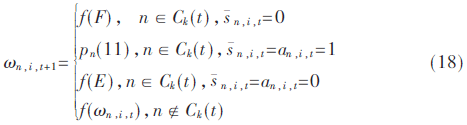
    (4)如果对于任意的信道i(i∈M)，有P_t(n，i)≥0.99，则此学习过程退出，否则继续步骤(2)，并以此进行其后操作。

4 仿真分析

    为验证本文提出的选择机制的优越性，设定了两种常用算法进行比较：单一的Q学习算法选择机制以及RMAB模型下常用的UCB算法。设定系统中信道数为10，用户数为4，并且不同时隙用户根据需求调整自己的选择信道的数目，使得系统内用户能够实现多信道接入(考虑到实际系统条件限制，设定每个用户最多选择信道数位3)。信道参数T=0.25 s，τ=0.01，β=0.95，用户数为3～15。

    图3显示在用户数为N=9时，不同冲突约束、不同算法中用户获得平均吞吐量的变化。从图中可以看出本文提出的信道选择机制能够很好地处理认知用户与主用户之间的冲突，使网络中各用户之间充分的使用信道资源，实现系统通信量的提升。同时，因为冲突约束越小用户选择信道的概率越小致使信道使用不充分，随着冲突约束的提升在保证用户选择的同时能够有效的避免与主用户的冲突，所以取15%作为系统冲突的限制，既能够保证认知用户选择，同时又能不对主用户通信造成干扰。

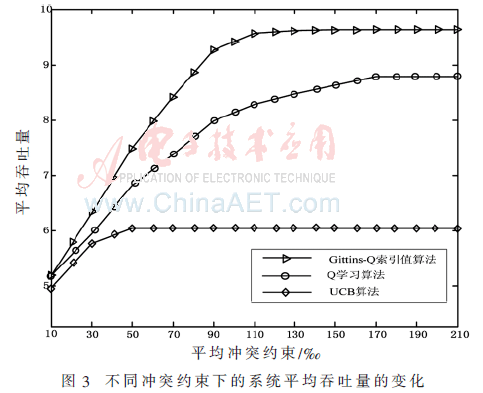
    图4显示了不同算法中采用不同认知用户数时系统内信道利用率的变化，从图中可以看出本文提出的算法能够取得很好的信道利用率。随着认知用户的不断增大，当用户数超过系统承受能力之后系统中认知用户之间会产生冲突，同时用户通信需求的扩大也会对主用户的通信造成影响，致使系统内信道使用率会有一定下降。

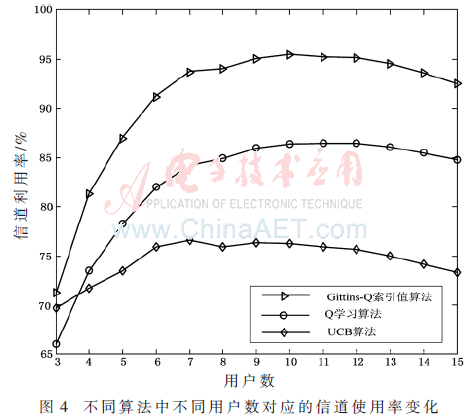
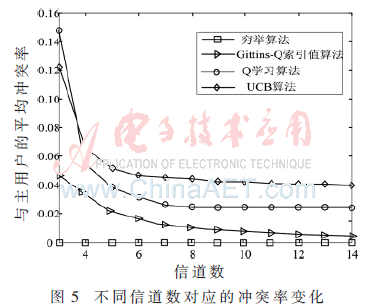
    图5显示的是在系统中干扰限制以认知用户数目固定的条件下(N=9，I_max=0.20)，随着系统中信道数的变化，认知用户与主用户产生干扰冲突的变化情况。从图中可以看出，本文提出的机制能够在较小范围内控制认知用户的信道选择，尽量避免与主用户的通信产生干扰，从图中可以看出随着系统中信道数目的增大，认知用户对主用户的干扰逐渐减小，也就是系统中认知用户选择信道的范围增大，选择空闲信道的概率增大。

5 结论

    本文中应用RMAB模型来搭建未知信息参数的网络系统，然后通过EMA算法实现用户对系统内信道使用情形的初步学习，然后借助Q学习算法实现了RMAB模型下的Gittins索引值求解，制定出了认知用户的信道选择策略，同时又能通过不断学习更新自身策略，最终实现系统内信道资源的充分使用，以及保证认知用户对主用户通信干扰的可控性。最终，仿真实验从多方面证明本文提出的选择机制能够很好地提高系统通信容量，使未知环境中的信道利用率得到明显提升。

参考文献

[1] Gao Yang，Wang Yiming.Multi-channel access algorithm with channel state information unknown[C].Intelligent Computation Technology and Automation(ICICTA)，2012 Fifth International Conference on.IEEE，2012：427-430.

[2] 张凯，李鸥，杨白薇.基于Q-learning的机会频谱接入信道选择算法[J].计算机应用研究，2013，30(5)：1467-1470.

[3] 刘振坤，鲜永菊.认知网络中基于竞价模型的频谱分配研究[J].计算机应用研究，2010，27(3).

[4] Raschellà A，Pérez-Romero J，Sallent O，et al.On the use of POMDP for spectrum selection in cognitive radio networks[C].Cognitive Radio Oriented Wireless Networks(CROWNCOM)，2013 8th International Conference on.IEEE，2013：19-24.

[5] LAN Z，JIANG H，WU X.Decentralized cognitive MAC protocol design based on POMDP and Q-Learning[C].IEEE International ICST Conference on Communication and Networking.2012：548-551.

[6] LAZAR N A.Statistical analysis with missing data[J].Technometrics，2003，45(4)：364-365.

[7] GITTINS J，GLAZEBROOK K，WEBER R.Multi-armed bandit allocation indices[M].John Wiley & Sons，2011.

[8] CHAKRAVORTY J，MAHAJAN A.Multi-armed bandits，gittins index，and its calculation[J].Methods and Applications of Statistics in Clinical Trials：Planning，Analysis，and Inferential Methods，2013(2)：416-435.