摘  要： 直线生成算法是计算机图形的基本算法，而现有算法都有其弊端，因此提出一种基于Bresenham任意宽度直线的生成算法。该算法首先根据直线的斜率、长度和宽度计算出直线所形成的边界，然后让单线宽直线沿着边界移动，使整个区域填充。该算法生成的直线两端与边界垂直，在直线斜率变化的情况下，直线宽度不会发生变化，且具有应用背景广泛、运算速度快、占用内存小等特点。

　　关键词： 直线生成；Bresenham画线算法；区域填充

0 引言

　　嵌入式图形系统的图形显示是通过光栅显示器来实现的，而光栅显示器实际上是一个像素矩阵，光栅显示器通过点亮一个个像素，确定最佳逼近于图像的像素集。直线是嵌入式图形系统中最基本的元素，因此直线生成算法也是其他各类图形算法的基础，得到了广泛的研究。现有的直线生成算法主要有：DDA算法、中点画线算法以及Bresenham算法等，其中应用最广泛的是Bresenham算法[1-3]，其优点是不需要进行小数和取整运算，只需要进行整数加法和乘法运算来计算出待生成的像素点的坐标。Bresenham算法是只针对于单像素宽的直线。而实际应用中，经常使用的线段是有线宽和线型的。对于多线宽直线的生成，目前国内外的研究不多，现有方案主要有线刷子算法、正方形刷子算法和区域填充算法。

　　线刷子算法原理：假设直线斜率在[-1，1]之间，垂直的长度线宽的线段中心对准线段起点，线段顺着单像素线条轨迹移动，直到末端。对于斜率绝对值大于1的，该刷子是水平方向的。线刷子算法具有算法简单、效率高的特点，但是刷子法生成的直线端点形状不理想，宽度小于指定宽度，而且宽度随斜率的改变而改变。

　　正方形刷子算法则是把边长为指定线宽的正方形沿着中心线平移，获得具有宽度的直线。与线刷子算法类似，其末端也是水平的或者垂直的，且线宽随线段斜率的改变而改变。

　　区域填充算法[4-6]则是使用改进的Bresenham计算出线段所形成矩形区域边界，画出封闭的区域，然后利用种子填充算法将矩形区域填充起来。其优点是生成直线端头标准，宽度可控，很接近理想多宽度直线。但是算法复杂，而且在背景与线段区域边界形成多分割区域时，容易形成填充孤岛，无法填充整个区域；填充过程中无法利用像素坐标之间的内在联系；且该算法应用于CAD/CAM造型系统，使用种子填充算法，占用内存大。

　　综上可以看出，以上算法都有其局限性，因此本文提出一种新的任意宽度直线的生成算法，该算法能够生成的任意宽度直线的末端与直线方向垂直，宽度可控，算法简单，占用内存小，适用背景广的任意直线算法，适合嵌入式设备。

1 算法思想与步骤

　　1.1 Bresenham算法

　　Bresenham算法是应用最广泛的直线扫描转换算法。其原理是：不考虑像素形状、大小的影响，经过各行、各列像素中心构造一组网格线，若直线斜率绝对值小于1，则按直线从起点到终点的顺序计算直线与各垂直网格线的交点，然后确定该列像素与此交点的最近像素；若直线斜率绝对值大于1，则计算与水平线的交点最近像素。该算法的优点在于采用增量计算，使得对于每一列，只要检查当前误差项的符号，就可以确定该列的所求像素。

　　Bresenhan算法误差项d递增如图1所示。设该直线的起始点为A（x1，y1），终点为B（xn，yb），则直线的斜率为K=dy/dx，dx=xn-x1，dy=yn-y1。从起点A，下一个像素的行坐标是x1+1，列坐标则递增1或者不变。是否增1，取决于图1所示误差项d的值。因为A点为图像的起点，图像经过其中心，所以误差项d的初始值为0。当x增加1，d的值相应递增直线的斜率K，即d=d+K，若d≥1，则减去1，让d始终在0~1之间。x1+1列像素中，到直线最近的点为C、D，C点到直线垂直距离A′C=1-d，D点到直线的垂直距离为A′D=d。当d>0.5时，则A′C<A′D，则C点距离直线更近，取C点；而当d<0.5时，D点更近，取D点；当d=0.5时，与上述两个像素一样近，约定取C点。为了避免浮点运算，将直线的斜率放大2×dx，K=dy/dx×2×dx=2×dy，误差项d=d+dy×2，当d>2×dx，则更靠近C（x1+1，y1+1）；当d≤2×dx，则更靠近D（x1+1，y1）。对于K>1，可以将坐标轴颠倒，根据Y变化计算X。对于K<0的情况，Y变化相反，那么X增加1，则Y的变化不变或减小1。通过递增运算，计算直线通过最近的每一个点，画出直线。

　　1.2 多线宽算法

　　（1）算法思想

　　任意宽度直线生成算法中，直线刷子法利用生成的单宽度直线，在直线沿Y轴移动到另一端（若直线的斜率在[-1，1]）。若直线斜率不在[-1，1]内，则改成沿X轴移动。而区域填充算法是使用Bresenham算法计算指定宽度直线的边界形成封闭区域，再进行利用种子填充算法填充，形成的直线两端标准。结合两种算法的优点，让单线宽线段沿着计算出的边界移动，即可以得到指定宽度的直线。

　　用内存存储每一列Y的增量，让单线沿着Bresenham算法形成的区域两端移动，因为线平行，计算它们连线只需要利用存储的Y的增量，产生新的直线，形成的直线两端垂直，且算法计算简单，没有种子填充算法的设定起始种子的局限。

　　（2）算法基本步骤

　　为了方便讨论，假设直线斜率在[0，1]之间，其他情况可以通过坐标轴变换得到。假设直线L的起点为O（x0，y0），其终点坐标为O′（x1，y1），令x1>x0，y1>y0，直线的宽度为D，并记终点O两侧的直线终点分别是A、B，点O′两侧的直线终点分别是C、D，且记直线AB为L1，直线CD为L2。

　　①根据给出的直线的首位坐标，计算出其dx和dy；

　　②根据指定的宽度，计算出其B与O点的偏移量，得出A、B的坐标；

　　③计算出AB直线中坐标增量，存入内存中；

　　④将点在AD、BC移动，根据内存中Y的变化量，计算出新的A′B′直线，直到到达另一个边界。

　　（3）直角保持与宽度控制

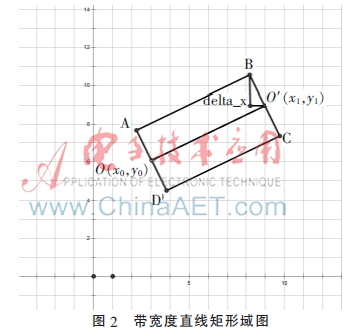
　　如图2所示，理想情况下直线OO′与直线BC、AD垂直，则可以推导出KBC×KOO′=-1。直线OO′斜率为KOO′=dx/dy，那么得到直线AD的斜率，则可以根据式（1）、（2）计算出边界点A与起点O的偏移量，由于ABCD是矩形，O′是B、C中点，O是A、D中点，则B、C与O′点的偏移量与A、D与O′的偏移量相等，因此得到A、B、C、D坐标。

　　dx2+dy2=（D/2）2（1）

　　-dx/dy=KAD（2）

　　平移AB用Bresenham算法计算出下一个端点B′点坐标时，直接使用OO′的dy代替AD的dx，OO′的dx代替AD的dy，保证AD最大限度垂直于OO′。BC直线上的做法相同，保证新产生A′B′的OO′与平行。这样就可以保证线段两端与线段垂直。

2 实验结果及分析

　　2.1 显示效果

　　图3是本算法生成的直线显示图。从图中可以看出，该算法产生的直线的两端与边界垂直，而且能很好地控制定制直线的宽度，使其在角度变化的情况下，直线宽度基本没有变化。

　　2.2 复杂度分析

　　以斜率绝对值小于1为例。设长度为a，宽度为b，则一共有a×b个像素需要点亮。其运算量主要在于计算像素点的坐标。在第一次计算完成边界线AB后，其Y坐标变化被存储起来，由于以后画出的直线与第一条直线平行，因此以后每次计算坐标只需要加上内存读取器Y坐标的变化0或者1。其复杂度近似为O（N）。

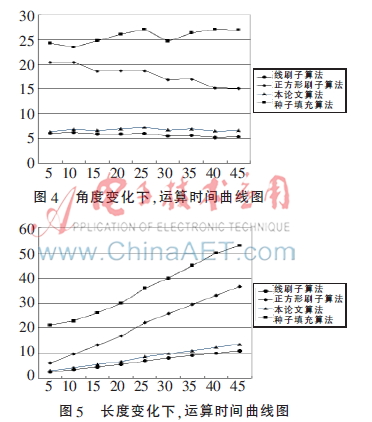
　　下面为本算法使用Keil软件在Cortex-M4内核下仿真的结果。其中图4为长度20、宽度5不变，角度变化下4种算法产生线段时间；图5为宽度5、角度30不变，长度变化下4种算法产生线段时间；图6为长度36、角度30不变，宽度变化下4种算法产生线段时间图。

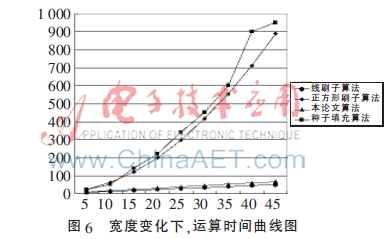
　　注：以上长度、宽度单位为像素，而角度单位为度，运算时间单位为微秒。

　　由于平行线采用的是线段平移，而且该线刷子法产生的多宽度直线的宽度小于实际直线，因此该算法的效率最高；而正方形刷子法由于像素大量冗余填写，因此其效率很低；而区域种子填充算法采用的是种子填充算法，需要频繁地出栈、入栈或者递归，因此效率也相对比较低。而本文提出的方法在效率上和线刷子法最接近，而且能够控制宽度，两端与直线完全垂直，产生很好的效果。

　　2.3 内存消耗分析

　　为了加快运算速度，本文中的线刷子算法使用内存存储单线段在X（dx>dy）变化下Y轴的变化量（1或者0），因此其使用的内存为dx，单位bit。正方形刷子算法不需要储存额外数据，不需要额外内存。种子填充算法需要出栈入栈，因此需要很大的栈空间。而本论文提出的算法同样采用这种方案加快运行速度，因此其使用与线刷子算法相同，额外占用的内存空间很小。

3 结论

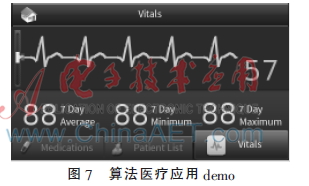
　　为了解决现存任意直线生成算法的弊端，提出一种基于Bresenham的算法。本算法首先计算出直线所形成的区域，然后利用斜率、长度相同单直线沿着边沿扫描整个区域，从而实现区域填充。该算法不仅始末端的效果好，宽度与理想直线接近，在斜率变化时基本不发生变化，而且算法复杂度小，适用于各种嵌入式设备中。图7是本算法应用在一嵌入式系统中的心电图demo实例，其中心电图的曲线是用几段直线替代的。

　　参考文献

　　[1] JAMES D F， ANDRIES V D ，STEVEN K F， et al. Computer graphics： principles， second edition in C[M].Pearson Education Press， 2004：21-35.

　　[2] BOYER V， BOURDIN J J. Auto-adaptive step straight-line algorithm[J]. IEEE Computer Graphics and Applications， 2000，20（5）： 67-69.

　　[3] 谢莹，许荣斌，赵宏坤.基于嵌入式图形系统的改进Bresenham反走样算法[J].计算机技术与发展，2006，16（11）：100-102.

　　[4] 骆朝亮，谢忠.一种快速的多线宽直线反走样算法[J].计算机工程与应用，2011，47（21）：188-190.

　　[5] 李震霄，何援军.任意宽度直线的绘制与反走样[J].武汉大学学报（工学版），2006，39（4）：130-133.

　　[6] 龙艳婷.任意宽度直线生成算法的研究与实现[J].沈阳工程学院学报（自然科学版），2012，8（4）：353-355，358.