摘 要: 校音器用于识别管弦乐器声音的基音频率和音高。该校音器使用型号为TMS320VC5509A的DSP芯片作数字信号处理,运行8192点快速傅里叶变换算法,实现声音信号频谱分析;利用语音编解码芯片TLV320AIC23将从麦克风获取的模拟信号转化为数字信号,采样率为 8 kHz;该检测仪利用LCD输出频率和音高信息;印刷电路板成品采用4层电路板模式。该检测仪可以有效检测管弦乐器的音域范围为32 Hz~4 kHz,频谱分辨率达到0.98 Hz。
关键词: 快速傅里叶变换;TMS320VC5509A;TLV320AIC23;声音基频检测;校音器
0 引言
校音器以声音基频检测技术为核心,用于检测乐器的音高是否标准。市场上流行的校音器精确度较低,音域的适应范围较小,实际的低音检测效果较差,而高品质校音器价格又过于昂贵。本文研发的作品力图挖掘数字信号处理器(Digital Signal Processor,DSP)和整体电路的性能,实现更精细的频谱分辨率,追求高精度与高可靠性;同时,更贴近管弦乐手用户的实际需求,提高校音专业性,完成高品质校音器,可广泛适用于管弦乐器的校音工作。
1 系统综述
该校音器用DSP为主芯片,以快速傅里叶变换(Fast Fourier Transformation,FFT)为核心算法,用于识别管弦乐器声音基音频率和音高,并判定乐器的音高是否标准。检测仪整个系统主要由传声器(麦克风,Mic)接口、模数转换器、数字信号处理器(DSP)、显示驱动和液晶显示屏(LCD)等模块组成,系统结构如图1所示。
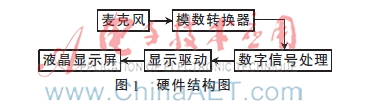
麦克风和模数转换器用于采集声音并转换成数字信号,DSP对数字信号进行快速傅里叶变换,得到振幅频谱数据、分析振幅频谱数据提取基音频率,并转化为音高。显示驱动通过复杂可编程逻辑芯片(CPLD)完成,并驱动LCD模块显示基音识别结果。
2 硬件电路设计
2.1 麦克风选择和模数转换器
为了提高音频识别效果,本文采用噪声低、拾音效果好的外接有源电容麦克风。麦克风频率响应为30 Hz~20 kHz,电源为48 V幻象电源。
模数转换器以音频编解码器(CODEC)芯片TLV320AIC23作为核心。该芯片有Line和Mic两种输入接口。如果录音设备功耗低,例如驻极体话筒,芯片上第17号管脚MICBIAS可为话筒提供偏置电压,大小为3/4 AVDD[1],用Mic接口接收信号。但这种话筒拾音性能差。为了降低输入噪声,提高拾音效果,本设计采用Line接口接收电容麦克风发送的音频模拟信号。Line连接方式原理图如图2所示。

图2中,TLV320AIC23B芯片上标号为D_90的第24号引脚与DSP TMS320VC5509APGE上第90号引脚相连,其他标号以此类推。闲置的引脚要悬空,不能接地。16号引脚用于降噪,由并联的去耦电容C19、C20完成。在每一个VDD引脚上并联这些去耦电容可以进一步降低电源噪声干扰。
2.2 数字信号处理器
该校音器采用型号为TMS320VC5509APGE的16位定点DSP负责数字信号处理。该DSP芯片时钟频率可达200 MHz,有128 K×16 bit片内RAM。
由于DSP内部存储器容量有限,因此需要使用bootloader将程序烧写到外部EEPROM中。通过合理配置GPIO的电平,上电时DSP会自动将EEPROM中的程序载入片内运行,这样就可以使DSP脱离仿真器和电脑而独立运行。
DSP最小系统电路与单片机相似,使用参考文献[2]所示电路。注意DSP内核需要1.8 V电源,外围数字芯片及数字高电平需要3.3 V电源,二者共用一个数字电路接地端。模拟电路也需要3.3 V供电电源和模拟电路接地端。虽然电压相同,但是数字和模拟电路要分开,数字地与模拟地之间用磁珠连接,以免干扰。
2.3 显示驱动和液晶显示屏
显示驱动采用型号为EPM240T100C5的CPLD芯片,图形点阵液晶屏模块为128×64像素。DSP使用EMIF接口与CPLD相互沟通,CPLD芯片电路基本按器件手册布局,此处不再赘述。
2.4 印刷线路板设计
校音器印刷电路板(PCB)采用4层布线,双面布件方式,核心器件布于顶层,部分器件布于底层,中间两层分别是地线层和电源层。PCB厂商要求PCB线宽线距8 mil以上,过孔内径12 mil以上,外径24 mil以上。成品如图3所示。图2中C5和C6电容优先布局,尽可能靠近引脚。C3和C4电容所在的两组信号线是电路中所有的模拟信号线路,优先布线。

3 软件设计
3.1 采样频率与FFT点数的选择
本系统使用8 kHz采样率和8 192点FFT。
科学音调记号法规定拉丁字母为音调,数字为八度区。钢琴音域由科学音调记号法表示为A0至C8,一般乐器常用音域是C1至B7,对应的频率范围是32.70 Hz ~3 951 Hz。交响乐队中,除了打击乐器,音高能超过钢琴的乐器不多,人类的歌喉很难逾越3 kHz。基于以上原因,该校音器测量范围设定在32.70 Hz~4 kHz。根据抽样定理,本系统的抽样频率选择8 kHz。
C1和C#1的频率分别为32.70 Hz和34.65 Hz,二者的几何平均为33.66 Hz,频谱分辨率最低要求为:
34.65 Hz-33.66 Hz=0.99 Hz
计算FFT采样点数如下:
采样点数=采样率÷频谱分辨率=8 000÷0.99=8 081
如果采样点数为8 192,则频谱分辨率为:
8 000÷8 192=0.98 Hz
一个八度分成12个半音音程,12平均律规定八度的音程(二倍频程)按频率等比例地分成12等份,两个相邻半音的频率大约为1.059 46倍[3],音高越高则频率相差越大。
因此,8 192点可以满足最低音高为C1、最高音高为B7的识别要求。
3.2 DSP算法实现
DSP代码分为5大部分,分别是声明定义、ADC、FFT计算、提取基音和LCD显示。主函数算法流程图如图4所示。
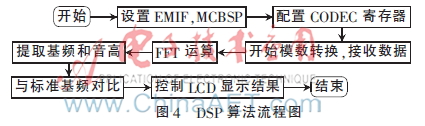
3.2.1 为变量分配存储空间
用于FFT运算的实型数组长度较大,需要占用很多空间。可以使用#pragma DATA_SECTION自定义段功能为变量分配存储空间。
首先,在源文件的开头,将数组sin_t安排在一个名为.databuf1的段中:
#pragma DATA_SECTION (sin_t,".databuf1")
float sin_t[8192];
之后,配置CMD文件。在MEMORY中定义区间SARAM3是一个起始地址为001c000h,大小为0005000h的储存空间:
SARAM3:origin=0016000h,length=0005000h
在SECTIONS中,将段.databuf1安排在区间SARAM3中:
.databuf1>SARAM3 fill=0
按如上方式分配,数组sin_t中所有的数据都保存在以0016000h为起始地址、长度为5000h的存储区里面[4]。按此规则,可以为所有变量和程序安排指定的存储空间。
3.2.2 FFT算法实现
FFT算法根据时间抽取基-2 FFT编程思想[5]。为了声音基频检测仪能够适应多种点数的FFT算法,本设计没有采用预设数据的方式,而是采用计算的方式对设置为全局变量的旋转因子进行初始化。初始化、倒位序和FFT运算的部分代码如下:
void InitForFFT(int point)/*旋转因子*/
//point为FFT点数
{
float PI=3.1415927;
float alpha,delta;
point >>= 1;
delta=PI/point;
alpha=0;
for(int i=0;i<point;i++)
{
sin_t[i]=sin(alpha);
cos_t[i]=cos(alpha);
alpha += delta;
}
}
/*倒位序,D_R为数据的实部*/
void invert(float*D_R, int point)
{
int i,j,k,LH,pt2;
float T;
LH=point>>=1; pt2=point-1; j=LH;
for(i=1;i<pt2;i++)/*point FFT点数*/
{
if(i<j)
{ T=D_R[i]; D_R[i]=D_R[j]; D_R[j]=T;}
k=LH;
while(j>=k) { j-=k; k>>=1; }
j=j+k;
}
}
/*FFT运算,D_I为数据的虚部,ORDER为阶数*/
void FFT(float *D_R,float *D_I, int ORDER){
int i,j,k,b,p,L;
float TR,TI,temp;
for (L=1;L<=ORDER;L++)
{
b=1<<(L-1);
for (j=0;j<b;j++)
{
p=(1<<(ORDER-L))*j;
for(k=j;k<point;k=k+b+b)/*蝶形运算单元*/ {
TR=D_R[k];TI=D_I[k];temp=D_R[k+b];
D_R[k]=D_R[k]+D_R[k+b]*cos_t[p]+D_I[k+b]*sin_t[p];
D_I[k]=D_I[k]-D_R[k+b]*sin_t[p]+D_I[k+b]*cos_t[p];
D_R[k+b]=TR-D_R[k+b]*cos_t[p]-D_I[k+b]*sin_t[p];
D_I[k+b]=TI+temp*sin_t[p]-D_I[k+b]*cos_t[p];
}
}
}
for(i=0;i<point;i++)
{
/*计算幅度谱*/
w[i]=sqrt(D_R[i]*D_R[i]+D_I[i]*D_I[i]);
}
}
代码中用到的整型变量ORDER是FFT级数,如 8 192点FFT是2的13次幂,ORDER就是13。以上算法理论上可以计算任意点数FFT,但是,受限于DSP5509芯片的存储空间和运算速度,FFT点数建议不超过 8 192。
3.2.3 基音频率分析
将经DSP运算得到的振幅频谱数据存于一个长度为8 192的16 bit无符号整形数组中。通过以下3步计算得到基因频率:
(1)消除白噪声:观察零输入状态下白噪声幅度可达到的最大值,以此定义最大值参数A,修改振幅频谱数据数组中的数据,保留数值大于参数A的视为有效信号,删除小于等于A的白噪声;
(2)从第一位开始寻找振幅频谱数据中第一个有效峰值所在位置;
(3)利用如下公式计算基音频率:
F=P×fs÷N(1)
其中,F为基音频率,P为有效峰值所在位置,fs为抽样频率,N为傅里叶变换点数。
利用TI公司的集成开发环境(Code Composer Studio,CCS)可以实时监控DSP的计算结果,其图像显示窗口可以为装有振幅频谱数据的数组作图。电子琴模拟小提琴声音演奏C5,CCS的图像显示窗口展示出幅度谱的前4 096点如图5所示。

图5中数据没有单位,横坐标代表数组的位置,纵坐标代表数组每一位对应的值,以十进制表示。
现实中的声音都是复合音。在声音的各个频率分量中,基音的频率是最低的,它决定声音的音高[6]。如图5中出现的第一个峰值为基音频率对应的位置,其横坐标为536。后3个峰值皆为泛音信号。根据式(1)计算基音频率为:
536×8 000÷8 192=532(Hz)
3.2.4 确定音高
音乐界已经明确规定了音高的基音频率。每个相邻半音之间的基音频率约是1.059 46倍。第5个八度的C,即C5附近部分音高频率举例如表1所示。

由于实际测试中获取的频率不可能与约定音高频率完全吻合,因此,采用判定频率区间的方式。频率区间的边界采用两个相邻音高频率的几何平均值。例如C5的频率区间为508 Hz~539 Hz。
通过频率区间确定音高后,再判断其与标准音高之间的误差。自定义误差值小于1/64倍,则认为准确,标注“YES”;如果检测频率误差超出范围,则用“-”表示音高偏低,用“+”表示音高偏高。
4 测试结果
用电子琴模拟提琴声音演奏C5,校音器检测结果如图6所示,图片在原图上进行了灰度和反色处理。图中显示“OK”表示基音频率标准。CCS显示幅度谱见图5。

C5的约定值是523.25 Hz,测量结果与理论结果相符。低音C2测量结果如图7所示,系统对低音的检测结果良好。
经过实际应用,该声音基频检测仪效检测的音域范围为32 Hz~4 kHz,对应管乐和弦乐的音高范围为C1至B7。
5 结论
该校音器可以用于大多数管乐器和弦乐器的校音工作,测试效果良好,可以从容面对诸如低音单簧管和大提琴的校音工作。得益于精细的频谱分辨率,校音器可精准分辨每个半音。电路板经过三次升级优化,成品整体电路性能较好。
参考文献
[1] 丁祥,余小清,万旺根.音频编解码器TLV320AIC23及其与DSP接口设计[J].单片机与嵌入式系统应用,2002(1):265-268.
[2] 汪春梅,孙洪波.TMS320C55xDSP原理及应用(第3版)[M].北京:电子工业出版社,2011.
[3] 胡泽.音乐声学[M].北京:中国广播电视出版社,2003.
[4] 陈泰红,任胜杰,魏宇.手把手教你学DSP-基于TMS320C55x[M].北京:北京航空航天大学出版社,2011.
[5] 焦瑞莉.数字信号处理[M].北京:机械工业出版社,2011.
[6] 胡泽.音乐声学[M].北京:中国广播电视出版社,2003.

