摘 要： 超分辨率重建通用方法中，图像分解后对应小波基只能有效稀疏表示单一成分，往往只侧重边缘成分而忽略了光滑成分等。针对这个问题，本文改进了一种基于压缩感知的声纳图像超分辨率重建算法。该算法基于三种不同稀疏字典小波变换模型，运用一种基于K-均值聚类算法的结构化字典训练法，并采用Newton-Raphson法进行迭代算法处理，实现声纳图像压缩感知的超分辨率重建。最后通过仿真实验，验证了此种算法的可行性和有效性。实验结果表明，该算法获得的超分辨率图像能够很好地重建并保持原图像的特征，能高效地改善并提高重建质量。
关键词： 压缩感知；超分辨率重建；稀疏字典；K-均值聚类算法；Newton-Raphson迭代法
0 引言
声纳图像技术以其系统的先进、稳定、高分辨率、高质量等优点广泛应用于各个领域中。而高分辨率的声纳图像可获得更全面更充足的水下情况信息，为声纳图像技术的应用提供更可靠的数据。要获得高分辨率图像，最直接的办法是采用高分辨率图像传感器。但由于传感器和光学器件制造工艺和成本的限制，在很多场合和大规模部署中很难实现[1]。
超分辨率（Super-resolution，SR）重建即通过序列低分辨率（Low-resolution，LR）图像获得高分辨率（High-resolution，HR）图像的过程。近年来，压缩感知与图像处理技术的融合已成为该领域的热点研究对象，各研究成果层出不穷，取得很大的进展。压缩感知理论指出：利用随机测量矩阵可把一个稀疏（或可压缩）的高维信号投影到低维（相对于高维）的空间上，并证明了这样的随机投影包含了重建信号的足够信息，即利用信号的稀疏性（或可压缩性）先验条件，通过一定的线性或非线性的解码模型可以以很高的概率重建原始信号[2]。近年来，基于字典学习方法的图像重建[3]成为各界学者研究的主流。
本文将压缩感知中的字典学习方法应用于声纳图像超分辨率重建中，改进了一种基于压缩感知多重稀疏表示的声纳图像超分辨率重建方法。该方法针对声纳图像所包含的光滑、边缘和纹理这三种形态信息特点，分别建立符合类内强稀疏且类间强不相干的过完备稀疏字典，并在传统字典学习的基础上，运用一种基于K-均值聚类算法的结构化字典训练法，且采用Newton-Raphson迭代算法快速求解交替迭代的运算过程。通过仿真实验验证了该方法在声纳图像重建中的可行性与有效性。
1 超分辨率模型、稀疏字典及重建
1.1 超分辨率模型
低分辨率图像由高分辨率图像经过相对运动、光学模糊、下采样或添加噪声等处理得到。具体在实际应用中表现为数字图像采集处理过程中的图像分辨率的下降，其主要现象为图像模糊、噪声与变形。
设第N帧低分辨率图像序列为{Vk|k=1，…，N}，每帧中的图像大小为：L=I1×I2。利用超分辨率图像重建，拟获得大小为M=r1I1×r2I2的高分辨率图像I，其中，r1、r2分别表示水平和垂直方向的分辨率提高因子，则超分辨率的通用退化数学模型[4]表示为：
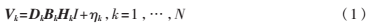
其中，Vk∈RL表示第k帧低分辨率图像，Ik∈RM表示原高分辨率图像，Hk表示Vk相对于I的运动变形矩阵，Bk表示光学模糊矩阵，Dk表示下采样矩阵，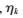
是系统引入的加性且均值为零的高斯白噪声。
1.2 稀疏字典
字典学习是通过稀疏表示来寻找最优基结构的过程，匹配且合适的字典可满足稀疏表示的各类约束，也能使信号获得更为精确的表示。字典学习主要包含两个关键问题：稀疏编码与字典更新。是否能够选取匹配的过完备字典与信号的稀疏性息息相关。通过训练样本来构建过完备字典从而确保信号稀疏性，是通用字典学习的算法之一。
1.3 压缩感知超分辨率重建
参考文献[5]提出了一种使用成分稀疏表示来实现超分辨率的方法，该方法在进行超分辨重建时，提取图像中的卡通成分和纹理成分，接着用两种不同的小波基对各自成分进行压缩感知。然而，基于形态学分析的图像，其卡通成分通常被分解为光滑成分和边缘成分，而一种小波基只能有效地稀疏表示一种成分，一般情况下只侧重边缘成分而忽略了光滑成分。但对于声纳图像来说，噪声在一定程度上影响了其成像效果，因此对声纳图像的光滑成分的研究对于超分辨率重建也起着重要的作用。
根据Meyer提出的卡通纹模式图像分解模型[6]，图像分解成光滑、边缘、纹理三种结构形态后，选用不同的过完备字典稀疏来表示每个成分。所选用的字典应尽可能匹配各部分的结构形态，且各成分的字典需保持类内强稀疏、类间不相干的特性。因此，根据离散平稳小波变换（Discrete Stationary Wavelet Transform，DSWT）[7-8]、轮廓小波变换[9]即塔型方向滤波器组（Pyramidal Directional Filter Bank，PDFB）、伽柏小波变换[10]建立对应稀疏字典。设图像I的光滑成分、边缘成分、纹理成分分别为Is、Ie和It，其对应的三个类内强稀疏且类间不相干的过完备字典为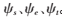
。
对于图像I，在过完备字典的作用下，其压缩感知稀疏表示为：
根据超分辨率退化模型，基于压缩感知的退化模型可表示为：
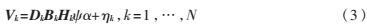
而超分辨率图像的重建是上述过程的逆过程，其过程表示为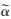
，则超分辨率图像可表示为：
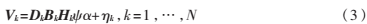
图像I的光滑、边缘、纹理三个成分分别为Is、Ie和It，对应三个类内强稀疏且类间不相干的过完备字典为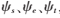
，可得图像压缩感知超分辨率退化模型如下：
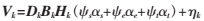
运用拉格朗日乘数法可求解压缩感知稀疏表示退化模型，得：
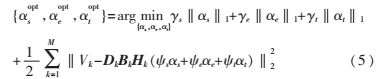
其中，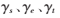
是用来平衡各部分比重的参数，其能够控制误差和稀疏性之间的平衡，而迭代过程中的方程模型可看做三个非线性凸优化问题，即可通过基追踪去噪法对其进行求解。
上述过程的逆过程为超分辨率图像的重建，则超分辨率图像的获得可表示为：
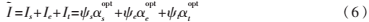
2 基于压缩感知的声纳图像超分辨率重建算法设计
基于压缩感知声纳图像超分辨率重建算法首先对原始图像进行K-均值聚类算法的结构化字典训练，得到光滑、边缘、纹理成分对应的过完备字典，然后运用Newton-Raphson迭代法求解图像退化模型中各成分的系数，最后通过超分辨率重建，获得重建图像。
2.1 本文基于压缩感知的声纳图像超分辨率重建算法实现
本文分别建立三个符合类内强稀疏且类间强不相干的过完备稀疏字典，运用一种基于K-均值聚类算法的结构化字典训练法，并采用Newton-Raphson迭代算法快速求解迭代过程，最后选取各数据重建声纳图像。
基于压缩感知的声纳图像超分辨率重建框图如图1所示。
综合算法步骤如下：
（1）输入原始图像I，图像维度M，平衡参数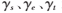
，迭代阈值N。
（2）对参数进行初始化设置：设光滑部分系数为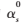
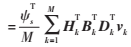，边缘部分系数
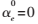，纹理部分系数为
。
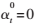（3）运用基于K-均值聚类算法的结构化字典训练法获得光滑、边缘、纹理成分对应的过完备字典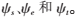
（4）运用Newton-Raphson迭代法稀疏表示退化模型中光滑、边缘、纹理成分的系数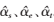
。
（5）输出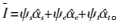
2.2 本文K-均值聚类算法的结构化字典训练算法的设计
字典训练方法有很多，如最大似然法、最优方向法、最大后验法等，而结构化的字典训练可以反映数据中隐藏的结构，并构造结构化字典，从而提高稀疏表示的精度。
运用一种基于K-均值聚类算法的结构化字典训练法作为综合算法获得各过完备字典的第一步。将字典中的原子平均分配到K个聚类中，并利用原子聚类索引计算得出拉普拉斯矩阵L，从而进一步利用GOMP算法[11]最后得到结构化过完备字典?鬃。
整个过完备字典训练过程算法如下：
（1）输入光滑成分对应初始过完备字典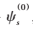
，聚类数Z，训练样本Ys，迭代阈值N0，正则化参数λs；
（2）对参数进行初始化设置：设迭代次数n=1，聚类中心矩阵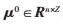
，J=1；
（3）将字典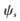
中的原子dj分到与聚类中心
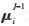最相似的Z个聚类集合中，并通过
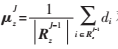对矩阵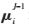
的第z列更新，其中，
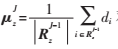
聚类集合可表示为：
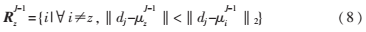
（4）J=J+1；循环（3）~（5）步，获得稳定聚类原子索引；
（5）根据原子索引d计算权重矩阵Ws、对角矩阵Cs及拉普拉斯矩阵Ls，并根据GOMP算法求出稀疏表示系数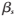
，最后更新字典
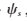，其过程为：
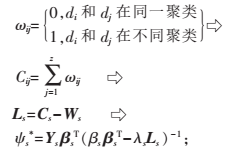
（6）n=n+1；循环（3）~（6）步至满足停止条件；
（7）输出光滑成分对应的过完备字典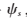
。
同理，运用该结构化字典训练法获得边缘成分及纹理成分对应的过完备字典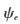
和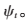
2.3 结合Newton-Raphson迭代算法流程
（1）根据式（5），恒定Ie、It，更新Is，计算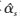
，具体表达式为：
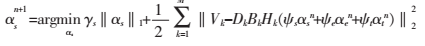
（2）同理，在恒定Is、It的条件下更新Ie，计算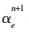
；在恒定Is、Ie的条件下更新It，计算
；
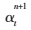（3）n=n+1；循环迭代直至满足阈值N时迭代停止。
（4）输出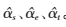
3 仿真结果及分析
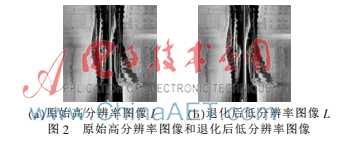
设图像维度为M，则选取：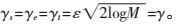
选择像素为256×256的原始高分辨率图像I，经过水平、垂直方向平移、高斯模糊、2倍率下采样及方差为15的高斯白噪声退化，生成128×128的低分辨率图像。原始高分辨率图像和退化后低分辨率图像如图2所示。
平衡参数rs=re=rt选取值为10，噪声方差为15时，分别用MSRSR法、未使用基于K-均值聚类算法的结构化字典训练一般方法及本文方法对图像L进行超分辨率重建。各方法重建效果如图3所示。
噪声方差为15时，重建结果的峰值信噪比变化函数及峰值信噪比的相对误差变化曲线如图4所示。
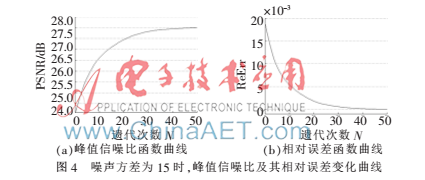
由图4可以看出，随着迭代次数的增加，峰值信噪比值先上升直至趋于平稳，相对误差值先下降直至趋于平稳。因此，为达到更好的实验效果，选取停止参数N>相对误差值时迭代停止。多次实验表明，10-4≤N≤10-3时，可得到较好的重建效果。因此，在重建实验中选取N=10-3。
实验中，在不同噪声方差的条件下分别使用MSRSR、一般字典训练重建法及本文方法来观察声纳图像重建的效果。具体比较结果如表1。
实验结果表明，三种方法都具有较好的重建效果。MSRSR法所得的峰值信噪比值略小于本文算法，而一般字典训练重建法的峰值信噪比与本文算法结果近似。但MSRSR方法更易受噪声影响，且由于稀疏字典与各成分匹配需要一定时间，因而本文算法的运行时间较长于MSRSR法；一般字典训练重建法运算时间较本文算法略大。即t一般字典训练法>t本文方法>tMSRSR。
4 结论
本文把压缩感知的方法运用到声纳图像超分辨率重建中，着重研究了超分辨率模型三种稀疏字典的建立，并结合K-均值聚类结构化字典训练法训练稀疏字典，最后采用Newton-Raphson迭代法求解图像退化模型中各成分的系数，代入超分辨率重建模型算法实现重建。实验结果表明该改进的基于压缩感知的超分辨率图像重建综合算法与传统的重建算法相比较，重建质量与效果在各个方面都有了较大的改善。
参考文献
[1] 王梁，郝燕玲，张振兴.基于多重稀疏表示的声纳图像超分辨率重建方法[J].系统工程与电子技术，2012，34（1）：204-207.
[2] 方红，章权兵，韦穗.基于非常稀疏随机投影的图像重建方法[J].计算机工程与应用，2007，43（22）：25-27.
[3] YAGHOOBI M， BLUMENSATH T， DAVIES M E. Dictionary learning for sparse approxunatuibs with the majorization method[J]. IEEE Tranansaction on Signal Processing， 2009，57（6）：2178-2191.
[4] NG M K， BOSE N K， Mathematical analysis of super-resolution methodology[J]. IEEE Signal Processing Magazine， 2003， 20（3）：62-74.
[5] 孙玉宝，韦志辉，肖亮，等.多形态稀疏性正则化的图像超分辨率算法[J].电子学报，2010（12）：2898-2903.
[6] MEYER Y. Oscillating patterns is image processing and nonlinear evolution equations[M]. Boston： Amer. Mathematical Society， 2001.
[7] ZHANG C， WANG X， ZHANG H. An intelligent algorithm for enhancing contrast for image based on discrete stationary wavelet transform and in-complete beta transform[C]. International Conference on Effective Computing and Intelligent Interaction， Beijing： Springer Verlog， 2005：135-143.
[8] WANG X H， ISTEPANIAN R S H， YONG H S. Microarray image enhancement by denoising using stationary wavelet transform[J]. IEEE Transaction on Nanobioscience，2003，2（4）：184-189.
[9] DO M N， VETTERLI M. Contourlets： a new directional multi-resolution image representation[C]. The Thirty-Sixth Asilomar Conference on Signals Systems and Computer， Pacific Groove， CA， United states： Institute of Electrical and Electronics Engineers Computer Society， 2002：497-501.
[10] 谢建辉.纹理特征提取与分类研究[D].武汉：华中科技大学，2008.
[11] 李祥灿.基于组稀疏表示的自然图像超分辨率算法研究[D].南京：南京理工大学，2014.