摘 要: 针对极端学习机算法对不平衡数据分类问题的处理效果不够理想,提出了一种基于聚类欠采样的极端学习机算法。新算法首先对训练集的负类样本进行聚类生成不同的簇,然后在各簇中按规定的采样率对其进行欠采样,取出的样本组成新的负类数据集,从而使训练集正负类数据个数达到相对平衡,最后训练分类器对测试集进行测试。实验结果表明,新算法有效地降低了数据的不平衡对分类准确率的影响,具有更好的分类性能。
关键词: 极端学习机;聚类;不平衡数据;欠采样;数据挖掘
0 引言
不平衡数据[1]是指在包含许多类别的大数据中,某些类别的数据个数远远小于其他类别的数据个数,即各类别数据的个数存在着不平衡性的数据。通常称样本数量少的类别为少类,也称为正类;样本数量多的类别为多类,也称为负类。在现实生活中,存在着许多不平衡数据的例子,如医疗诊断病变信息、垃圾信息过滤、故障检测等。正如这些实例,少数类数据所包含的信息往往是我们所需要的。因此,怎样更好地提取这部分数据,已成为数据挖掘研究中的一个热点话题。
目前,不平衡数据的分类问题的处理方法[2]主要可分为两类:数据层面上,主要是对原始数据集进行处理,利用少数类过采样、多数类欠采样、混合采样等方法使得原始数据集各类别数据个数达到相对平衡,主要方法有过采样技术(Synthetic Minority Oversampling Technique,SMOTE)[3]、单边选择欠采样技术(One-sided Selection)[4]等;算法层面上,主要是对已有分类算法进行改进或是设计新算法使其有效地解决不平衡数据分类问题,主要算法有支持向量机(Support Vector Machine,SVM)[5]、Bagging算法[6-7]等。
极端学习机作为一种分类算法,具有训练速度快、泛化性能好等特点,但其对不平衡数据分类问题的处理效果并不理想。本文提出了一种基于聚类欠采样的极端学习机分类算法。为方便起见,本文主要考虑数据二分类的问题。算法首先利用聚类原理对训练集中的负类样本进行聚类生成不同的簇,并计算各簇数据与簇中心的距离并排序,然后在每个簇中按规定的采样率取出距离中心近的数据,与训练集的正类一起组成类别相对平衡的数据集,最后训练分类器,预测测试集数据所属类别。新算法有效地解决了数据的不平衡性对分类器性能的影响,具有较强的实用性,并在实例数据实验中得到了证实。
1 理论分析
1.1 极端学习机算法(ELM)
极端学习机(Extreme Learning Machine,ELM)[8-9]是一种快速的单隐层前馈神经网络训练算法。该算法的特点是随机选取输入权值向量及隐层神经元的偏置,在训练的过程中,只需要设置隐层节点的个数,便可通过一个简单的线性系统求出唯一的最优解。
对于N个不同的训练集数据(xi,ti)∈Rn·Rm,其中xi=(xi1,xi2,…,xin)T为数据样本点,ti=(ti1,ti2,…,tim)T为类别标签,隐层节点数为M,激活函数为g(x)的单隐层前馈神经网络的输出函数表达式为:
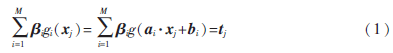
其中,j=1,2,…,N,ai=(ai1,ai2,…,ain)T表示连接输入节点和第i个隐层节点的输入权值向量,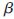 i=(
i=( i1,
i1,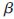 i2,…,
i2,…, im)表示连接第i个隐层节点和输出节点的输出权值向量,bi表示第i个隐层节点的偏置。g:R→R为激活函数,ai·xj表示输入权值向量ai和样本xj在Rn中的内积。
im)表示连接第i个隐层节点和输出节点的输出权值向量,bi表示第i个隐层节点的偏置。g:R→R为激活函数,ai·xj表示输入权值向量ai和样本xj在Rn中的内积。
假设这个函数可以以零误差逼近这个不同的数据样本,也就是说,存在参数(ai,bi)和?茁i使得:

那么问题就转化为求H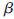 =T的最小二乘解
=T的最小二乘解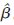 。当M≥N时,矩阵H可直接求逆;当M<<N时,由Moore-Penrose广义逆可以得到:
。当M≥N时,矩阵H可直接求逆;当M<<N时,由Moore-Penrose广义逆可以得到:
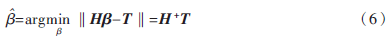
其中H+=(HTH)-1HT为H的广义逆矩阵。
最小二乘解 即为输出权值,所求解问题最终转化为求解一个矩阵的广义逆问题。与传统的分类算法相比,ELM算法能一次性求出输出权值,不需要任何迭代过程,减少了调节参数的时间,从而提高了运算速度。
即为输出权值,所求解问题最终转化为求解一个矩阵的广义逆问题。与传统的分类算法相比,ELM算法能一次性求出输出权值,不需要任何迭代过程,减少了调节参数的时间,从而提高了运算速度。
ELM算法的主要步骤:
(1)输入训练集(xi,ti)∈Rm×Rn,激活函数为g(x),隐层节点个数为M;
(2)随机生成输入权值向量ai和偏置bi;
(3)计算隐层输出矩阵H;
(4)由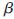 =H+T,计算输出权值
=H+T,计算输出权值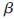 ;
;
(5)输入测试集Y={yi},激活函数为g(x),隐层节点个数M;
(6)调用输入权值向量ai和偏置bi,隐层输出矩阵H,输出权值 ,由
,由 =H+TY,计算测试集的标签TYT。
=H+TY,计算测试集的标签TYT。
1.2 模糊聚类算法(FCM)
模糊C均值聚类算法(Fuzzy C-Means,FCM)[10-11]于1981年被Bezdek提出,是一种柔性的模糊划分。它的思想是将数据集划分为不同的簇,用值在0,1间的隶属度来确定每个数据属于某个簇的程度,要求同一簇的对象之间相似度尽可能大,而不同簇的对象之间相似度尽可能小。
给定有限数据集X={x1,x2,…,xn},FCM算法将n个数据xi(i=1,2,…,n)分为C个簇,并求每个簇的聚类中心,使目标函数达到最小。其目标函数如下:
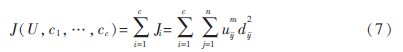
其中,uij∈(0,1),ci为第i簇的聚类中心,dij=‖ci-xj‖,表示第i个聚类中心与第j个数据点间的欧氏距离,m∈[1,∞)是一个加权指数。其约束条件为一个数据集的隶属度的和等于1,即:

由拉格朗日乘子法,构造新的目标函数:

由条件极值,使式(7)达到最小的必要条件为:
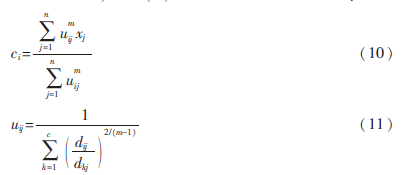
2 基于聚类欠采样的极端学习机算法(FCM-ELM)
定义1 设训练集的正负类样本个数分别为P、F,聚类个数为C,聚类后各簇的样本个数为p1,p2,…,pc,则规定第i簇的采样率为:

本文算法的主要步骤:
(1)计算训练集的正负类样本个数,分别记为P、F,利用FCM算法对训练集的负类样本进行聚类,生成C个簇;
(2)聚类后各簇的数据按到各自聚类中心的距离由小到大排序,并且输出按顺序排列的各簇数据集;
(3)对各簇按规定的采样率ni进行欠采样处理,每个簇中取出离聚类中心最近的ni个样本,取出的C×ni个样本组成新的负类数据集;
(4)将新的负类数据集和正类数据集合并作为新的训练集,训练极端学习机分类器,最后预测测试集的标签。
3 不平衡数据分类性能的评价指标

表1是数据二分类问题的混淆矩阵,TP、TN分别为分类正确的少数类和多数类的样本个数,FN、FP分别为分类错误的少数类和多数类的样本个数。
不平衡数据分类性能评价指标的相关定义如下:
定义2 正类样本的查准率(Precision):

(3)ROC曲线(Receiver Operating Chara-cteristic)[14]:
ROC曲线是分类器整体分类性能的评价标准,该曲线能很好地反应两类数据分类错误率之间的关系。但ROC曲线不能定量地评价分类器的性能,所以利用ROC曲线下的面积AUC(Area Under the Curve)来评估分类器性能。AUC值越大,分类器性能越好,反之越差。
4 实验结果及分析
本文实验所用的8个数据集均来自于UCI机器学习数据库,每个数据集多类与少类样本数量的比例失衡程度不同,具体信息如表2所示。
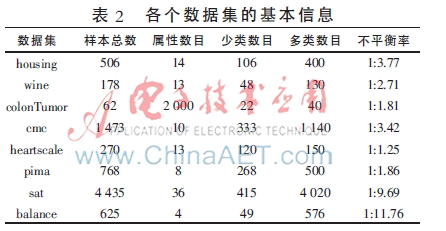
实验中,采用十折交叉验证方法将数据集分为训练集和测试集,选用ELM算法、FCM-ELM算法进行对比实验。两种算法的激活函数均选择Sigmoid函数,隐层节点数设为200。训练集、测试集的划分存在一定的随机性,为了充分证明算法的有效性,实验结果均取循环100次后的平均值。此外,FCM-ELM算法实验中,聚类中心个数C分别取3、5、9、15。以上算法均在MATLAB R2012a上实现。在G-means、F-measure、AUC三种评价指标下,两种算法的实验结果对比如表3~表5所示。
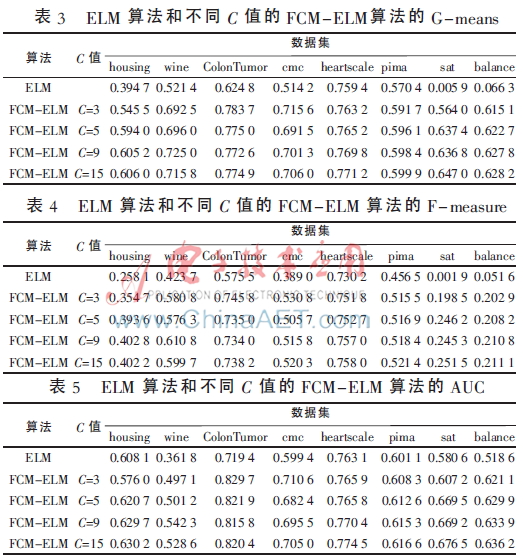
从表3~表5可以看出,FCM-ELM算法的准确率明显优于ELM算法。在前六个比例失衡程度较小的数据集中,准确率最多提高了20%,最后两个比例失衡程度较大的数据集中,准确率最多提高了63%。而且,当聚类中心个数C取不同的值时,FCM-ELM算法的实验结果相差较小,相对比较稳定。
5 结束语
本文针对不平衡数据的分类问题,提出了一种基于聚类欠采样的极端学习机算法。该方法首先对训练集的负类样本进行聚类,然后按规定的采样率进行欠采样,使得训练集正负类样本个数达到近似平衡,有效地解决了原始的极端学习机算法对不平衡数据分类的错分问题。将新算法用于实例数据集的分类问题中,其有效性和优越性得到了证明。
参考文献
[1] Han Jiawei, KAMBER M.数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2001.
[2] 王和勇,樊泓坤,姚正安,等.不平衡数据集的分类方法研究[J].计算机应用研究,2008,25(5):1301-1308.
[3] CHAWLA N V, BOWYER K B, HALL L Q, et al. SMOTE: Synthetic minority over-sampling technique[J].Journal of Artificial Intelligence Research, 2002(16):321-357.
[4] KUBAT M, MATWIN S. Addressing the curse of imbalanced training sets: one-sided selection[C]. Proceedings of the 14th International Conference on Machine Learning, San Francisco, 1997:179-186.
[5] VAPNIK V. The nature of statistical learning theory[M].New York: Springer-Verlag, 2000.
[6] 秦姣龙,王蔚.Bagging组合的不平衡数据分类方法[J].计算机工程,2011,37(14):178-182.
[7] 李明方,张化祥.针对不平衡数据的Bagging改进算法[J].计算机工程与应用,2013,49(2):40-42.
[8] HUANG G B, ZHOU H, DING X, et al. Extreme learning machine for regression and multiclass classification[J]. IEEE Trans. Syst. Man Cybern, 2012,42(2):513-529.
[9] HUANG G B. An insight into extreme learning machines random neurons, random features and kernels[J]. Cognitive Computation, 2014,6(3):376-390.
[10] BEZDEK J. Pattern recognition with fuzzy objec-tive function algorithms[M]. New York: Plenum Plenum Press,1981.
[11] 肖景春,张敏.基于减法聚类与模糊C-均值的模糊聚类的研究[J].计算机工程,2005,31(Z1):135-137.
[12] 林智勇,郝志峰,杨晓伟.若干评价准则对不平衡数据学习的影响[J].华南理工大学学报,2010,38(4):126-135.
[13] 杨明,尹军梅,吉银林.不平衡数据分类方法综述[J].南京师范大学学报:工程技术版,2008,8(4):7-12.
[14] BRADLEY A P. The use of the area under the ROC curve in the evaluation of machine learning algorithms[J].Pattern Recognition, 1997,30(7): 1145-1159.

