0 引言

    锂离子电池具有超长寿命、使用安全、大容量、绿色环保、无记忆效应、体积小、质量轻等其他动力电池无法比拟的优点，从而成为电动汽车动力电池的首选之一^[1-3]。由于电池的制作工艺、初始充电的状态不一致、散热条件不同、环境气温的变化等原因，都会导致电池的分散性^[4-5]，引起串联电池的充放电特性不同。因此，动力电池组在串联充放电过程中，为了使单节动力电池不过充、不过放，以延长动力电池的使用寿命，必须对单节动力电池电压等参数进行检测，并对单节电池的剩余容量（SOC）进行估计^[6]。

    动力电池的剩余容量的估计与电池的电压有很大关系。大量在电动汽车电池剩余电量估计上的研究都依赖于电池的开路电压^[7-8]。由于这些研究方法并没有考虑电化学电池的参数变化，使得估计的准确度取决于电池的健康状态(SOH)、寿命影响以及生产中的缺陷。加之，电池使用过程中开路电压并不容易获得，因而这些方法并不足够准确以至于结果可能对电池的正常充电和性能造成危害，这将造成电池热崩溃。还有一些方法则是依赖于电池的充放电状态电流或是电池的内部阻抗，而这些方法存在误差大、结果不可靠的问题。

    本文提出了一种基于脉冲响应[9]的电池端电压检测方法来预测锂离子电池端电压的方法，通过实验验证了该种检测方法的有效性和可靠性，为电池的剩余容量估计提供了一种有效的工具。

1 锂离子电池等效电路模型

    锂离子电池是一种可充电电池，一般使用锂合金金属氧化物为正极材料，如LiCoO₂、LiMnO₄等，石墨为负极材料，使用非水电解质。相比于其他类型的电池，锂离子电池保持电量的能力更好，在同样大小的电池中也更轻便，并且其不具有记忆效应，不必在充电前完全放电。所有的这些优点表明选取锂离子电池作为电动汽车的动力电池是一种很好的选择。

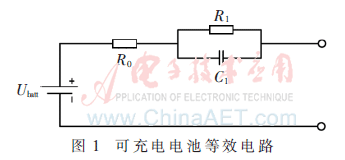
    锂离子电池的等效电路一般常采用Thevenin等效电路模型，如图1所示。其中，R₀为欧姆电阻，R₁、C₁分别为电池的极化内阻和极化电容，U_batt为电池的开路电压。该模型考虑了电池电压在充放电流激励下的突变性和渐变性特点，由R₀来等效模拟电压突变的电阻特性，由R₁和C₁组成惯性RC环节对应电压的渐变特性。此外，为使建模简化，不考虑温度和电流内阻等的影响。

2 脉冲响应思想及方法描述

2.1 脉冲响应思想

    函数f与函数g的卷积由f*g表示，其基本定义是某一在t时刻的函数与另一在t-ζ时刻的函数相乘的积分（整个域的独立变量，即时间），表达式如下：

    由于卷积是可交换的，所以首位函数的选取并不重要。

    由线性系统理论可知，对于任意的一个输入，线性时不变系统的输出均可由它的脉冲响应确定，表达式如下：

    其中，x[k]、h[k]和y[k]分别代表系统的输入、脉冲响应和输出。即系统的输入与它的脉冲响应的卷积将得到系统的输出。

    为了确定电池的脉冲响应，向电池施加一个电流脉冲并对电池的输出电压作检测，结果如图2所示。

    电池的脉冲响应可作为电池模型并取代电池来计算输出电压。将电池的脉冲响应与任意的输入电流作卷积，可计算得到输出电压：

    其中i[k]、h[k]和v[k]分别代表电池的端电流、脉冲响应和端电压。

2.2 ARMAX模型

    自回归移动平均模型(ARMAX)^[10-11]可以用数字形式来表示离散线性时不变系统的脉冲响应。对于单一输入/输出的系统(SISO)，给出了ARMAX的多项式模型结构：

    其中，y(t)代表在t时刻的输出，u(t)代表在t时刻的输入，e(t)是白噪声干扰，q^-1是反向移算子。并满足：

    其中，n、m和r分别是多项式的阶数，为估计出ARMAX模型需要先确定合适的模型阶数。针对指定的模型，采用电池的输入电流作为模型的输入u(t)，而利用多项式可计算出输出电压y(t)。

2.3 方法描述

    针对模拟锂离子电池模型，本文采用基于电池的脉冲响应方法，而电池的脉冲响应又取决于电池的剩余容量(SOC)。不同的SOC对应于不同的脉冲响应。必须注意的是在固有的脉冲当中电流脉冲的持续时间要远远小于系统中的最小时间常数。图3表示的是比克18650锂离子电池的SOC为80%时的脉冲响应。

    计算出不同SOC值所对应的电池脉冲响应并存储于查找表中，即电池的整个SOC的可取范围由单个i值所对应的特定脉冲响应h_i[k]进行分区。实验中，向电池施加一个输入电流，而电池产生的输出电压响应将对应于该特定电流。将电池的脉冲响应存储于查找表中，任意输入电流的端电压均可通过输入电流与查找表当中所存储的脉冲响应的卷积得到。因此就有，对于任意输入的i值，输出电压的求解式表达如下：

    然后，将由查表获得的脉冲响应而计算出的电压与实际所测量得到的输出电压作比较，确定出合适的与电池相关的脉冲响应。因为已知不同的SOC值对应于相应的脉冲响应，从而可以确定出电池的SOC。图4表示的是所提出方法的结构框图。

3 实验结果

    实验所用电池：比克18650锂离子电池，容量为2.2 Ah，标称电压为3.7 V，实验环境温度为25 ℃。图5和图6分别表示了SOC=75%和SOC=20%时的电池的脉冲响应。结果表明对于不同的SOC的电池其脉冲响应是不同的。

    利用Battery Design Studio仿真工具所得到的仿真结果对该方法进行验证。向18650锂离子电池模型施加一脉冲幅度为1 A、脉冲宽度为1 s的充电电流脉冲，对不同SOC的电池进行测试，由所获得的脉冲响应数据可知, 同一输入电流脉冲下，不同SOC的电池，其输出电压脉冲响应不同，数据表如表1所示。

    同时，对于同一SOC级而言，脉冲响应也会受到施加的电流脉冲幅度的影响。因而对不同的SOC级的电池选取不同的充电电流脉冲来估测其脉冲响应，其结果如表2所示。表2给出了SOC值分别为60%和80%时，输入电流脉冲宽度为1 s，脉冲幅度分别为0.5 A、1 A和1.5 A的电压响应数据表。

    根据已确定的电池的ARMAX模型，对SOC为100%的18650锂离子电池施加脉冲幅度为3.8 A、脉冲宽度为200 s的放电电流脉冲，图7所示为对应放电电流脉冲的电池的输出电压。

    利用图7的放电脉冲，在SOC为100%测试下电池的ARMAX模型的估计如下：

    表3为不同SOC情况下，分别对电池的ARMAX模型和软件模型施加脉冲幅度为1 A、脉冲宽度为1 s的输入充电电流脉冲的输出电压的对比。由表可知，两模型的输出电压误差较小且小于0.5%，充分验证了基于脉冲响应的这一检测方法的可靠性。

4 结语

    本文提出了一种基于脉冲响应的电池端电压在线检测方法，由ARMAX模型来真实反映电池的脉冲响应状态，根据电池的SOC不同其脉冲响应不同以及同一SOC的电池输入脉冲不同其脉冲响应不同来预测电池的端电压，仿真结果和实验结果充分验证了该方法的有效性和可靠性。利用该种方法为电池的剩余容量估计提供一种有效的工具，并且针对不同的电池类型，该方法也同样适用。

参考文献

[1] 卢杰祥.锂离子电池特性建模与SOC估算研究[D].广州华南理工大学，2012.

[2] 赵庆河.一种电动车用锂电池剩余容量检测系统[J].信息技术，2012(6)：205-207.

[3] 田晓辉，刁海南，范波，等.车用锂离子动力电池SOC的预测研究[J].电源技术，2010，34(1)：51-54.

[4] 李哲.纯电动汽车磷酸铁电池性能研究[D].北京：清华大学，2011.

[5] SHIN H C，PARK S B，JANG H，et al.Rate performance and structural change of Cr-doped LiFePO4/C during cycling[J].Electrochimica Acta，2008，53(27)：7946-7951.

[6] 李国进，董第永，陈双.磷酸铁锂电池的SOC预测[J].计算机仿真，2015，32(3)：163-168.

[7] SINKARAM C，RAJAKUMAR K，ASIRVADAM V.Modeling battery management system using the lithium-ion battery[C].Control System，Computing and Engineering (ICCSCE)，2012 IEEE International Conference on IEEE，2012：50-55.

[8] BOWKETT M，THANAPALAN K，STOCKLEY T，et al.Design and implementation of an optimal battery management system for hybrid electric vehicles[C].Automation and Computing(ICAC)，2013 19th International Conference on IEEE，2013：1-5.

[9] 郭永刚，许亮华，水小平.基于脉冲响应数据的armax法建模以及模态参数识别[J].地震工程与工程振动，2006，26(5)：167-171.

[10] 辛斌，白永强，陈杰.基于偏差消除最小二乘估计和Durbin方法的两阶段ARMAX参数辨识[J].自动化学报，2012，38(3)：491-496.

[11] 王宏伟，于双和.基于模糊ARMAX模型的模糊建模[J].控制理论与应用，2009，26(1)：85-88.