摘 要： 针对传统的滤波器设计方法效率低、方法复杂、不能满足高效高精度的需要等缺点，基于MATLAB研究了分别使用窗函数法和双线性变换法的FIR和IIR滤波器。将加入噪声的信号分别通过两种滤波器，滤除加入的噪声，对滤波前后的信号进行对比分析。通过仿真实验表明，FIR滤波器与IIR的Butterworth滤波器都能很好地克服传统滤波器的不足，通过语谱图直观地对比发现基于窗函数法设计FIR滤波器比双线性法设计的Butterworth滤波器能更好地达到预定的去噪效果。
0 引言
在噪音信号处理过程中，所处理的信号往往混有噪音，从接收到的信号中消除或减弱噪音是信号传输和处理中十分重要的问题[1-3]。常用去噪方法有图像去噪法、信号去噪法、小波去噪法等。郑毅贤利用压缩感知图像去噪法能够有效地保留较多的图像细节[4]；谢黎明等人设计出基于MATLAB的IIR数字滤波器，分析表明该 IIR滤波器具有良好的去噪性能[5]；张廷尉等人设计出基于MATLAB的Butterworth数字低通滤波器，并对一段音频信号进行滤波去噪处理，经过去噪后的音频信号听觉效果变得低沉[6]。数字滤波器分为2类：无限冲击响应（IIR）滤波器和有限冲击响应（FIR）滤波器。FIR滤波器具有稳定性好、精度高、积累误差小、易于计算机辅助设计等优点[7-8]，但存在计算量大的缺点。IIR滤波器具有结构简单、效率高、与模拟滤波器有对应关系、易于解析控制及计算机辅助设计等优点[9]，但稳定性较差，易产生溢出、噪声、误差。利用数字滤波器，可改变信号中所含频率分量的相对比例或滤除某些频率分量。
本文基于MATLAB分别使用窗函数法和双线性变换法设计FIR和IIR滤波器，将加噪信号分别通过两种滤波器滤除噪声，对滤波前后的信号进行对比分析。仿真实验表明，基于窗函数法的FIR滤波器去噪效果比双线性法设计的IIR滤波器好。
1 加噪处理
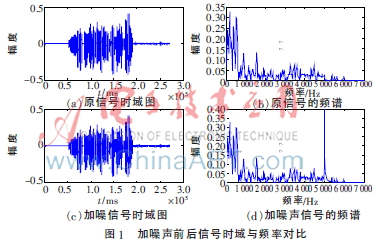
预先录制一段语音，内容为“基于MATLAB的语音信号处理及特性分析”，人声的频率范围为300 Hz~ 3 000 Hz，3 kHz以上的频率分量属于采集过程中由于设备和环境而引入的噪声。人声的频率范围低于3 kHz，且通过观察原信号的频谱可得，频率为5kHz的频率分量能量较小，因此选择加上频率为5 kHz的高频余弦噪声并且绘制叠加噪声之后的语音信号时域图形及频域图形，可以在视觉上与原始信号图形对比。使用subplot函数将加噪声前后的信号时域与频率图画在同一幅图上进行对比，如图1所示。与原始信号对比，加噪信号能量明显变大，且在频率为5 kHz的位置能量有了很大的增强。使用sound函数播放加噪语音信号，语音的背景出现尖锐鸣声，这是由加入的余弦噪声造成的，鸣声的尖锐程度取决于余弦噪声的频率，但如果频率过高，超过人耳的听力范围，就无法察觉加噪信号。余弦噪声是单一频率的、高频的，为了滤除噪声，只需要将噪音信号通过一个低通滤波器，就可将余弦噪声及录制过程中引入的噪声滤除。
2 窗函数法设计FIR滤波器
数字滤波器可以分为IIR数字滤波器和FIR数字滤波器。与IIR数字滤波器相比，FIR数字滤波器的实现是非递归的，稳定性好，精度高。更重要的是FIR数字滤波器在满足幅度响应要求的同时，可以获得严格的线性相位。然而，由于阶次较高，FIR滤波器的延迟也要比同样性能的IIR滤波器大得多。
窗函数法设计FIR滤波器，使用fir1函数，B=FIR1（N，WN，′FTYPE′，WINDOW）。其中：
（1）N为滤波器的阶数；
（2）WN为滤波器的截止频率，是一个0~1的数。如果WN是含有两个数的向量，则函数返回一个带通滤波器；
（3）FTYPE=′HIGH′时，设计的是高通滤波器，FTYPE=′STOP′时，设计的是带阻滤波器，无此参数时，默认为低通滤波器；
（4）WINDOW为指定窗函数，矩形窗为BOXCAR（N），汉宁窗为HANNING（N），海明窗为HAMMING（N），布莱克曼窗为BLACKMAN（N），凯撒窗为KAISER（N，BETA），无此参数时，默认为HAMMING窗。
窗口选用HAMMING窗，因为它给出比较小的过渡带，有较低的阶。其中滤波器长度N=133，通带截止频率为0.25π，阻带截止频率为0.3π，通带衰减0.027 8 dB，阻带衰减52 dB，幅度响应曲线如图2所示。
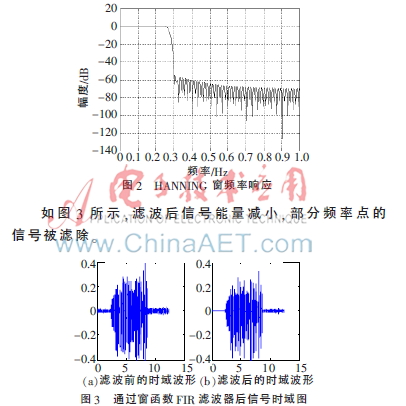
如图4所示，原信号频谱图中在6 kHz以下的频率均有信号的存在，但是人声的频率上限为3 kHz，判断 3 kHz以上的信号均是因设备和环境而引入的噪声，滤除余弦噪声时需一并滤除。由加噪声后的频谱图知在 5 kHz的频率点上出现一个峰值，这是通过加噪处理加入的噪声；由滤波后的频谱图知通过窗函数法设计的FIR滤波器后，频率高于3 kHz的信号被截止，低频的语音信息被保留下来。因设备、环境引入的3 kHz以上的噪声，以及加入的余弦噪声均被滤除，播放过滤后的语音信号，已经听不到尖锐的高频声音，证明噪声被成功滤除，原始信号基本被还原。
图5中，在原信号语谱图中5 kHz以下且从2 s~9 s时段范围内，信号颜色为红色，9 s~12 s间呈淡黄色；加噪后语谱图中5 kHz以下且从2 s~9 s这段范围内，信号颜色基本为红色，在滤波后的语谱图中3 kHz以下且2 s~9 s这段范围内颜色为红色。
将原信号、滤波前后信号的语谱图进行对比，其中代表加入余弦噪声的红色谱线滤波后变成蓝绿色，且 3 kHz以上的谱线基本为蓝绿色，甚至是蓝色。参照颜色条，蓝绿色、蓝色的谱线能量非常低，与3 kHz以下的红色谱线形成鲜明对比，可以直观地看到3 kHz以上的噪声信号被滤除。
3 双线性变换法设计Butterworth滤波器
Butterworth滤波器是IIR滤波器的一种，本文以Butterworth滤波器的设计进行说明。
在工程上常用的设计模拟滤波器方法分别是脉冲响应不变法和双线性变换法。
双线性变换法在实际中采用最为普遍，其设计准则是使数字滤波器的频率响应与参考模拟滤波器的频率响应相似。设计步骤如下：
（1）确定数字滤波器的性能指标。这些指标包括：通带、阻带临界频率wp、ws；通带内的最大衰减Rp；阻带内的最小衰减As；采样周期Ts。
（2）将模拟指标转换成数字指标，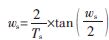
，
。
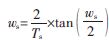（3）计算上述参数给出的滤波器阶数N和截止频率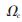
，从而求得低通原型的传递函数Ha（s）。
（4）将
，求得数字滤波器传递函数：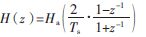
用双线性变换法设计数字Butterworth低通滤波器，采样频率为22 050 Hz，其中通带截止频率wp=0.20π，阻带截止频率ws=0.24π，通带内衰减Rp=1 dB，阻带内衰减As=15 dB。
Butterworth滤波器频率响应曲线如图6所示。
如图7所示，与通过FIR滤波器相似，滤波后信号时域波形幅度减小，能量减小，某些频率点信号被滤除。
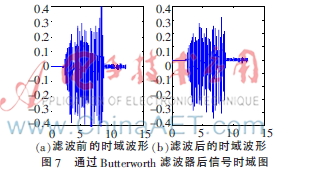
如图8（c）所示，频谱图上频率3 kHz以上的信号被截止。图9中，在原始信号语谱中5 kHz以下且在2 s~9 s时段范围内，信号颜色为红色，9 s~12 s间呈淡黄色；加噪后语谱图中5 kHz以下且2 s~9 s时段范围内，信号颜色基本为红色，在滤波后的语谱图中3 kHz以下且在2 s~9 s时段范围内颜色为红色。
语谱图上3 kHz的谱线基本为蓝绿色，但是在某些时刻，3 kHz附近一些谱线为黄色甚至红色。虽然两种类型的滤波器得出频谱图基本一样，但是通过语谱图直观地对比发现，相对于使用窗函数法设计的FIR滤波器，用双线性法设计的Butterworth滤波器稍微逊色一点。但如果从听觉感受上评价，两种滤波器都能成功滤掉尖锐的噪声，滤波效果都是相当不错的。
4 结论
利用MATLAB软件平台强大的运算功能，应用窗函数法和双线性变换法可快速有效地设计FIR和IIR滤波器，将加噪信号分别通过两种滤波器，滤除加入的噪声，对滤波前后的信号进行对比分析，仿真实验表明，基于窗函数法设计的FIR滤波器比双线性法设计的Butterworth滤波器能更好地达到预定的去噪效果。
参考文献
[1] 赵颖，刘祖深，李胜寅.基于MATLAB的FIR数字滤波器的方法设计[J].国外电子测量技术，2012，31（10）：35-37.
[2] 严慧，于继明.基于Matlab的IIR数字滤波器设计[J].软件导刊，2013，12（1）：110-113.
[3] 张萍.基于DSP的IIR低通数字滤波器的设计与实现[J].江南大学学报（自然科学版），2014，13（1）：67-79.
[4] 郑毅贤，江浩淼，金波，等.基于自适应压缩感知的图像去噪方法[J].通信技术，2013（3）：74-76.
[5] 谢黎明，郑锐.基于Matlab的IIR数字滤波器设计[J].机械与电子，2011（1）：28-30.
[6] 张廷尉，陈红，王磊.基于Matlab的巴特沃斯数字低通滤波器的设计[J].鞍山师范学院学报，2012，14（2）：13-15.
[7] 凌春丽，刘云飞，姜黎黎，等.二维滤波器分布式算法结构的改进与实现[J].中北大学学报（自然科学版），2012，33（2）：154-158.
[8] 李兰英，王志超,王峰,等.FIR数字滤波器设计与仿真[J].哈尔滨理工大学学报，2013，18（3）：36-41.
[9] 韩泽欣，杨雪松.基于Matlab的数字滤波器设计[J].甘肃科技，2013，29（5）：9-10.