摘 要： 有组织犯罪集团挖掘是目前数据挖掘技术研究的热点，利用共犯网络结构提出一种新的有组织犯罪集团挖掘的方法。该方法能从大型真实犯罪数据集获取有组织犯罪集团信息，提高了有组织犯罪集团检测效率。实验结果表明，该方法能分析出有组织犯罪集团特征演变轨迹，对挖掘有组织犯罪集团证据可行、有效。
关键词： 数据挖掘；共犯网络；有组织犯罪集团；检测效率
0 引言
共犯网络结构分析是理解有组织犯罪成因和干预策略影响的关键，即如何在共犯网络结构基础上对有组织犯罪集团证据进行挖掘[1]。本文抓住有组织犯罪集团检测计算方法的关键——共犯网络，利用小团体的扩展渗透法匹配犯罪集团中的某个单元，提出了共犯网络分析视角（Co-offending Networks Analysis Perspective，CNAP）算法，并在大型真实犯罪数据集进行实验。实验结果表明，在共犯网络结构分析上，该方法极大地提高了有组织犯罪分析计算速度，而且保持了较高的有效性。
1 概念
定义1 罪犯组
指3人以上为了实施一种或几种犯罪而组织起来的共同犯罪组织，定义模型中，C1t，C2t，…，Cnt指n个罪犯组在时间t的共犯网络。
定义2 有组织犯罪集团
在理论上[2]，有组织犯罪集团和犯罪集团的两个概念至少在3个基本方面不同：（1）组织规模和动机；（2）合作的时间间隔；（3）犯罪活动的类型。然而在实践中，有组织的犯罪集团和犯罪集团之间的区别并不总是清晰的，这也给研究带来了许多挑战。在以下模型中，用O1t，O2t，…，Omt表示在时间t共犯网络中有m个有组织犯罪集团。
2 有组织犯罪集团检测
2.1 罪犯组检测
该方法的第一步是建立K-结点的罪犯组网络，彼此共享至少k-1结点的相邻K-结点网络[3]。假设k=3，因为有组织犯罪集团至少有3个成员，每个组可能属于不同的独立社区但有共同交叉结点，因此该罪犯组既有重叠的成员还有普通成员。将这些成员分配到每个罪犯组形成内核K（Ci），内核是一个犯罪集团主要的成员，是完全参与该犯罪组活动。第二步，将邻居结点直接连接到内核添加到罪犯组，这些结点被称为外围，用 P（Ci）表示。
2.2 有组织犯罪集团检测
犯罪活动和犯罪行为是理解犯罪集团组织结构两个关键特征[4]。下面提出两个操作算子对犯罪活动和行为进行计算。
犯罪集团Ci在时间t犯罪行为表示为![A)]8YVKJHTB0`W@2AB$E64W.jpg](http://files.chinaaet.com/images/2016/02/23/6359185340910000002579066.jpg "A)]8YVKJHTB0`W@2AB$E64W.jpg")
（Ci），定义为：
其中，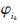
表示某个罪犯ik的严重程度，即犯罪集团Ci成员在t时刻的犯罪行为。
设i1，i2，…，in是Ci在时间t的犯罪成员，犯罪集团C在时间t1到时间t2的活动记为
，计算公式如下：
其中，|Rt1（Ci）|和|Rt2（Ci）|分别表示犯罪集团Ci在时刻t1和时刻t2共犯次数。
为了确定发现罪犯组是否被认为是有组织犯罪集团，必须同时考虑犯罪活动和犯罪行为，定义两个阈值：
表示犯罪活动和
表示犯罪行为。如果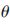
（Ci）>
，那么给定的犯罪集团C就是活动的犯罪集团A；如果
（Ci）>
，那么C就是一个严重犯罪集团。
2.3 有组织犯罪集团演化模型
这个模型需要确定原来的某个犯罪集团已经演变当前的某个犯罪集团。一个犯罪集团的一个周期会出现5个阶段：产生、分裂、合并、出现和终止[5]。为此，引入一个匹配的函数F：
其中，
表示一个犯罪组织集合，2
表示
的幂集。给定一个有组织犯罪集团Oit和有组织犯罪集团集合
t+1，如果F（Oit，g）得出集团Oit+1与Oit有最大的交集超过给定的阈值![{AWDTO2HL]2LLVSUN78HLCH.png](http://files.chinaaet.com/images/2016/02/23/6359185413131900009534935.png "{AWDTO2HL]2LLVSUN78HLCH.png")
，形式定义如下：
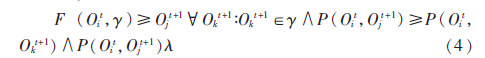
这里两个有组织犯罪集团O，O′∈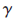
，P（O，O′）定义如下：
算法1 有组织犯罪集团检测
输入：
（1）犯罪事件数据集；
（2）Crime seriousness index（犯罪程度索引）；
（3）犯罪活动和犯罪行为的阈值：α，β。
输出：有组织犯罪集团O1t，O2t，…，Omt
（1）/*数据准备*/；
（2）扫描在[t1，t2]时间之间每个犯罪事件集；
（3）抽取共犯网络；
（4）检测犯罪组织C1t，C2t，…Cnt；
（5）对每个犯罪组织Cit∈Ct做第（6）步和（7）步；
（6）计算组织犯罪活动阈值
（7）计算组织犯罪行为阈值![}{WY{%046O[S[]8F34GI6]V.png](http://files.chinaaet.com/images/2016/02/23/6359185422055500004264902.png "}{WY{%046O[S[]8F34GI6]V.png")
（8）对满足阈值的犯罪组织标识为有可能组织犯罪集团；
（9）对每个犯罪组织候选集Oit，进行第（10）步；
（10）评估出犯罪组织物质利益；
（11）对有组织犯罪集团，O1t，O2t，…，Omt，应用演变跟踪模型。
3 实验结果
3.1 犯罪数据集
为了验证方法的有效性，实验数据采用加拿大不列颠哥伦比亚省arrest-data犯罪数据集[6]，该数据集记录了从2001-8-1至2006-7-31共5年的犯罪数据。
图1显示了活跃罪犯组的数量随着第1、2、3、4这4段时间观察到的区别。值得注意的是，随着时间的推移，活跃犯罪组的数量急剧下降。在a值较高时从一个时间段到下一个时间段连续活动明显可见，这一发现印证了犯罪组织的短期合作的理论[7]。
3.2 罪犯组演变
因为不知道第一步以前的历史时间和最后一次未来时间，在有限的可观测时间跨度里对罪犯组的整个生命周期进行量化工作非常困难[8]。
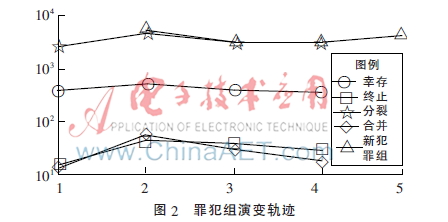
在5个不同时间段各罪犯组的演化轨迹统计如图2所示。匹配函数的阈值0.3适用于考虑幸存一组，值大于0.2和小于0.3分别适用于分裂和合并，组匹配阈值小于0.2被认为是终止罪犯组。总体而言（平均而言），所有罪犯群体大约14%幸存，但分裂和合并事件很少发生，不到犯罪组的1%。大约88%的罪犯组被认为是终止了，因为在接下来的时间并没有观察到他们的活动，所有组织中90%是新出现的犯罪组。
4 结论
为提高有组织犯罪集团证据计算效率，本文提出基于共犯网络结构分析技术。实验结果表明，虽然罪犯在犯罪集团中的合作是连续的，但大多数犯罪组织的活动不会持续很长时间。另外，活跃的犯罪组织通常有更多的外围，相比之下严重的犯罪组织外围成员偏少，这一发现表明，严重犯罪组织的运作主要来自他们的内核成员。在未来的工作中将探索有组织犯罪的组织结构，区分层次组织和分散组织，并分析这些结构演变轨迹。
参考文献
[1] MCGLOIN J M， NGUYEN H. The importance of studying co-offending networks for criminological theory and policy[C]. Proceedings of Third Annual Illicit Networks Workshop， Montréal， Québec， October 2011.
[2] KIM M S， HAN J W. A particle-and-density based evolutionary clustering method for dynamic networks[J]. Proceedings of Very Large Data Base Endowment， 2009， 2（1）： 622-633.
[8] KIM K， MCKAY R， MOON B R. Multiobjective evolutionary algorithms for dynamic social network clustering[C]. Proceedings of the 12th Conf.Genetic and Evolutionary Computation， 2010：1179-1186.
[3] SATULURI V， PARTHASARATHY S. Scalable graph clustering using stochastic flows： applications to community discovery[C]. KDD， Paris， France， 2009：737-746.
[4] INOKUCHI A， WASHIO T. Mining frequent graph sequence patterns induced by vertices[C]. Proceedings of the SIAM Int′1 Conference on Data Mining， 2010：466-477.
[5] MICHELLE G， NEWMAN M E J. Community structure in social and biological networks[J]. PNAS， 2002，99（12）：7821-7826.
[6] TAYEBI M A， GL?魧SSER U. Organized crime structures in co-offending networks[C]. Proceedings of International Conference on Social Computing and its Applications， Sydney， Australia， Dec. 2011.
[7] NGUYEN N P，DINH T N，Ying Xuan， et al. Adaptive algorithms for detecting community structure in dynamic social networks[C]. Shanghai： Proceedings of IEEE Infocom′11， 2011：2282-2290.
[8] BACKSTROM L， HUTTENLOCHER D， KLEINBERG J， et al. Group formation in large social networks： membership， growth and evolution[C]. Proceedings of the KDD， 2006： 44-54.