摘  要： 提出一种基于OFDM水声信道模型的信道自适应稀疏度估计方法。该方法利用小波分解估计得到信道初始稀疏度，结合已有的压缩感知自适应算法的思想确定算法迭代停止条件完成信道估计，解决实际运用中水声通信系统信道估计时稀疏度未知的问题。仿真实验结果表明，所提出的方法可精确重构估计信道信息，大大减少自适应算法的运行时间。

　　关键词： 压缩感知；水声信道估计；OFDM；自适应；小波分解

0 引言

　　水声通信过程中时延扩展和多普勒频移严重影响水声通信系统的通信性能，只有获得准确的信道状态信息，才能保证通信的性能，这使得信道估计成为水声通信系统中的关键技术。压缩感知理论突破了传统的信号采样方式，利用信号自身的稀疏特性，在采样的同时进行信号压缩，通过信号重构算法利用少量的采样信号可以精确恢复原信号。水声信道的稀疏性质使压缩感知理论可以应用到水声信道的估计问题。

　　由于水声信道的脉冲响应能量通常集中在少量的主要路径上，这样就使得信道响应系数大部分为零或接近于零[1]。近年来，国内外学者利用水声信道固有的稀疏特性提出了许多基于压缩感知的稀疏信道估计方法[2-3]，相对于传统的信道估计算法可以节约水声通信系统中宝贵的频率资源[4]。但这些算法需要已知信道的稀疏性质。本文提出利用小波分解估计得到信道初始稀疏度，并结合已有的压缩感知自适应算法的自适应思想，准确估计得到信道的状态信息。

1 水声稀疏信道估计方法

　　一个典型的OFDM水声通信系统如图1所示。

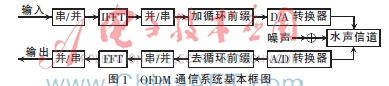
　　传统的OFDM系统的信道估计方法是基于导频辅助的信道估计方法，其过程就是在发送端信号适当位置插入导频，接收端用导频信号同时估计得到当前位置的信道信息，再利用内插、滤波等技术手段得到整个信道的信道信息[5]。但是由于通信信号中引入导频信号，占用信道的带宽，降低了整个系统频带利用率。

　　水声通信信道的稀疏特性符合压缩感知的使用前提，可以将水声信道估计问题看成稀疏信号的重构问题来解决。

　　假设OFDM水声通信系统的发射信号为X，接收信号为Y，那么整个通信系统可以简化为如下模型：

　　Y=XH+N（1）

　　其中H表示信道的状态矩阵，是稀疏的，而输入X和输出Y都已经知道，结合CS理论，就可以运用压缩感知的恢复算法估计得到H。

2 压缩感知及重建算法

　　压缩感知是一种可以用稀疏信号的压缩测量值来恢复原信号的新的采样理论[6]。

　　压缩感知的数学模型如下：

　　其中，是一个M×N维的感应矩阵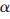，是一个N×1维的稀疏度为S的向量，R是一个M×1维的压缩信号向量，N为高斯白噪声。根据压缩感知原理可得，如果一个向量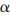是稀疏的或者近稀疏的，那么就可以设计一个矩阵通过对信号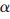的线性投影得到测量值R，这样就可以通过较少的M个测量值来恢复。

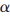　　以OMP算法和CoSaMP算法为例，传统的压缩感知重建算法对信号进行重建时都需要信号的稀疏度k作为先验信息输入，才能够完成信号的重构。然而，信号的稀疏度在实际通信过程中不容易得到，尤其是在水声通信系统中，水声信道时变空变的特性让水声信道中信号的稀疏度也在不停地变化，因此，有文献提出了自适应的重建算法，此类算法不需要稀疏度k作为先验信息输入就可以完成信号的重建。例如SAMP[7]算法就是一种典型的自适应的重建算法。

　　SAMP算法首先确定固定步长，算法迭代时对残差值r进行比较，残差r在迭代过程中总是越来越小，因此可动态地探测并逼近信号的实际稀疏度k。

　　自适应的压缩感知重建算法不需要稀疏度k作为先验信息输入，但算法的计算量很大，不易收敛，重建信号的时间较长，实际应用价值也大打折扣。

3 提出的方法

　　由上面介绍的压缩感知重构算法可以看出，传统的重构算法的终止条件都是根据稀疏度来确定的，可是在实际的水声通信系统中，多径信道的稀疏度是未知的，自适应的压缩感知重构算法虽然能够在信号稀疏度未知条件下对信号进行重构，但是这种自适应算法的计算量比较大，算法收敛比较困难。为了能够找到一种在稀疏度未知情况下对信号重建并且能够减小算法的计算复杂度的方法，本文提出的方法将重构恢复算法分为两部分，首先采用小波分解技术预先估计得到水声信道的稀疏性，再结合自适应的算法完成整个信道估计过程。

　　因为信号里包含了噪声，对信号做小波分解后，噪声主要集中到了高频分量中，即高频部分的小波系数里包含噪声能量，高频的小波系数称为细节系数。而对噪声的估计结果可以用下面的公式得到[8]：

　　其中，di是利用小波分解估计得到的在频域的细节系数。

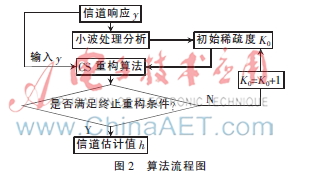
　　用估计得到的噪声能量作为一个阈值，用来确定信号中信号的能量集中的抽头个数，为了保证确定抽头个数的准确性，可以将阈值设得高些，只估计得出明显的路径数。用估计得到的路径数目作为初始稀疏度，最后根据自适应算法确定算法迭代的停止条件，完成整个信道信息的估计。整个算法流程如图2所示。

4 MATLAB实验结果及分析

　　为了说明本文提出的方法能够有效地重构出原始信号，将文中提出的信道估计方法结合贪心算法经过MATLAB仿真平台进行验证。

　　仿真采用OFDM信道模型，具体参数如表1所示。

　　实验比较了OMP和CoSaMP恢复算法在本文预测稀疏性方法下与已知稀疏度两种情况下的性能。仿真结果图3所示。

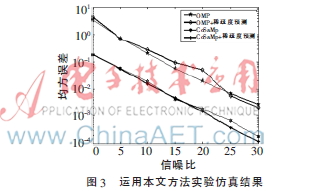
　　仿真实验的结果显示，随着信噪比的增加，OMP算法和CoSaMP算法的均方误差逐渐减小，由于CoSaMP算法具有较好的抗噪声性能，因此在本文提出的稀疏度自适应方法条件下，CoSaMP算法比OMP算法的性能更好。与已知稀疏度条件下的算法相比，二者之间的性能相差不大，证明了本文提出方法的有效性。

　　另外，本文还比较了在不同导频数目条件下，CoSaMP算法结合提出的方法与传统的最小二乘（Least Square，LS）方法的性能比较。本文对比选取导频数目分别为：16、32、48，结果如图4所示。

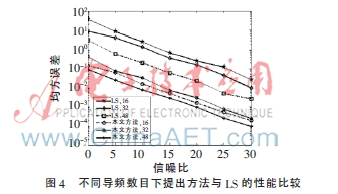
　　图4结果显示，传统LS信道估计算法随着导频数目的增加，其算法的性能越来越好，但结合本文提出方法的自适应压缩感知算法在不同导频数目下的性能都比LS算法要好。另外，自适应算法在不同导频数的性能基本差不多。因此，压缩感知理论可以利用较少的导频达到很好的性能。

　　压缩感知算法收敛速度快，这是在信号稀疏度已知的条件下达到的。而自适应的重构算法计算比较复杂，收敛时间较长。本文提出的方法能够大大减少自适应算法的计算量，能够更快地收敛，实现信号重构，这对压缩感知的实际应用是十分有意义的。本文提出的方法结合自适应算法的运行收敛时间与其他算法的比较如表2所示。

　　从表2可以看出各种算法在稀疏度已知情况和使用本文方法后的运行时间，通过对比可知，对于传统的重构算法而言，使用本文方法进行信道估计，虽然会增加算法的计算量，使重构算法收敛时间变长，但是对于自适应的算法来说，却可以减少算法的运行时间。传统的算法不适用于水声特殊的信道环境，自适应的算法的稀疏度自适应性具有实际的应用价值，而本文的方法可以加快自适应算法的收敛时间，有实际的使用价值。

5 结论

　　本文提出一种基于压缩感知的自适应稀疏度水声信道估计方法，该方法运用小波分解估计信道初始稀疏度，结合已有的自适应恢复算法完成整个信道估计算法，解决实际通信系统中信道稀疏度未知的问题。实验结果表明，该方法能够有效地恢复原信号，加快自适应算法的收敛。但是相对于直接输入稀疏度的算法而言，该方法程序运行的时间比较长，这是进一步需要改进的地方。此外，如何准确快速地估计信号的稀疏度也是需要进一步研究的内容。

参考文献

　　[1] STOJANOVIC M， PREISIG J. Underwater acousticcommunication channels： propagation modes and statistical characterization[J]. Communications Magazine， IEEE， 2009，47（1）：84-89.

　　[2] BERGER C R， ZHOU S， PREISIG J C， et al. Sparse channel estimation for multicarrier underwater acoustic communication： from subspace methods to compressed sensing[J]. IEEE Transactions on Signal Processing， 2010，58（3）： 1708-1721.

　　[3] 何雪云，宋荣方，周克琴.基于压缩感知的OFDM系统稀疏信道估计新方法研究[J].南京邮电大学学报（自然科学版），2010，30（2）：60-65.

　　[4] LAKSHMI K， MURALIKRISHNA P， SOMAN K P. Compressive estimation of UWA channels for OFDM transmission using iterative sparse reconstruction algorithms[C]. 2013 International Multi-Conference on Automation， Computing， Communication， Control and Compressed Sensing（iMac4s），  IEEE， 2013： 847-851.

　　[5] 殷敬伟.水声通信原理及信号处理技术[M].北京：国防工业出版社，2011.

　　[6] BERGER C R， Wang Zhaohui， Huang Jianzhong， et al. Application of compressive sensing to sparse channel estimation[J]. Communications Magazine， IEEE， 2010，48（11）：164-174.

　　[7] DO T T， GAN L， NGUYEN N， et al. Sparsity adaptive matching pursuit algorithm for practical compressed sensing[C]. 2008 42nd Asilomar Conference on Signals， Systems and Computers， IEEE， 2008：581-587.

　　[8] Wang Han， Huang Jianguo， He Chengbing， et al. An efficient sparse channel estimation method with predetermined sparsity[C]. TENCON 2013-2013 IEEE Region 10 Conference （31194）， IEEE， 2013：1-5.