摘要：提出了一种基于时空密度聚类的隐马尔科夫模型对时空序列进行预测的方法。时空序列与一般的时间序列相比，最主要的特征是其时空依赖性以及时空非平稳性。针对如何有效地预测不同尺度分布的时空序列的问题，本文采用基于时空密度聚类的隐马尔科夫模型，该模型不仅能分析时空序列在时间和空间上的相关性，而且可以通过时空序列的分段有效地去除噪声，提高模型预测的精度。本文采用该模型对药品冷藏库中的时空序列温度数据进行分析预测，并与其他预测模型比较，结果显示本文提出的方法更准确有效。

　　关键词：密度聚类；隐马尔科夫模型；时空序列预测

0引言

　　近年来国内外对时间序列的分析研究［1］取得了很多重要的研究成果，但是对时空序列的分析研究还比较少。时空序列是时间序列在空间上的扩展，是指在空间上有相关关系的多个时间序列的集合，时空序列数据是具有空间信息的时间序列数据集。

　　目前对时空序列数据［2］的建模与预测方法大致可以分为两类：基于时序的预测方法，如时空自回归移动平均模型(STARMA)、时空神经网络(STANN)、时空支持向量机(STSVM)［3］等；基于因果预测方法，如地理加权回归(GWR)［4］等。STARMA模型只适合对平稳时空序列进行预测，然而大多数时空序列在时间域和空间域上都显示着非平稳的特征；STANN模型和STSVM模型虽然预测效果较为不错，但是它们有一个共同点，即模型对历史样本的依赖程度非常大，而时空序列经常出现波动，错误的样本会严重影响预测的精度。GWR方法是一种局域空间分析的方法，展示了研究区域内部空间关系的变化，对研究区域整体趋势有一定的局限性。

　　本文提出一种基于时空密度聚类［5］的隐马尔科夫模型（Hidden Markov Model,HMM）［6］对时空序列进行预测。首先采用CP-PLR算法［7］对原始时空序列进行分段，然后采用基于时空密度的聚类方法对时空数据进行聚类，最后通过隐马尔科夫模型进行数据预测，将预测结果与其他模型的预测结果相比较，验证了该模型的高精度性、高有效性。

1问题建模

　　针对本文的情况，假设给定一个空间内的一个时空序列，其在二维空间内的分布情况如图1所示。

　　本文采用隐马尔科夫模型对时空序列进行预测，模型运行的原理是在原始时空序列中获得模型所需要的隐状态序列，而获得隐含状态的序列就需要先解决对原始时空序列的聚类问题。由上图可知，时空序列在空间内的分布不均匀，如果将时间与空间分别进行相似性的度量，不能很好地结合二者，而且聚类后的结果具有很大的偏差，这样将导致预测精度严重降低。

　　根据时空序列时间和空间上的邻近性，在时空聚类分析中，传统的距离度量准则难以直接用来描述时空实体间的相似性，本文需要采用特殊的时空聚类方法，该聚类方法在兼顾时空相关性的同时还能很好地对时空序列进行度量，而密度的概念对此是可以直接适用的。要得到基于时空密度聚类的隐马尔科夫模型，首先必须解决以下几个问题：（1）如何将原始带噪声的时空序列很好地分段而且达到去噪的目的；（2）如何将分段后的时空序列根据时空相关性进行聚类。

2算法架构

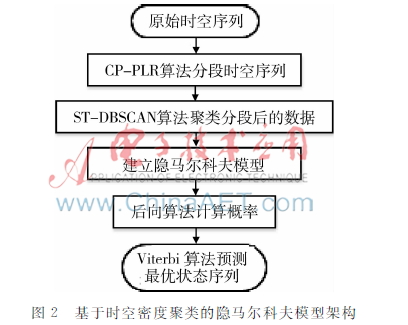
　　基于时空密度聚类的隐马尔科夫预测模型的整体架构如图2所示。首先采用分段算法将原始时空序列进行分段，然后采用STDBSCAN算法对分段数据聚类，利用聚类的结果建立隐马尔科夫模型，最后对时空序列进行状态预测。　

3时空序列的聚类

　　时空序列数据与一般的时间序列数据和空间数据相比，时空依赖性(或相关性)、时空异质性(或非平稳性)是其最主要的特征。时空数据是时间和空间的组合，空间数据和时间序列的一些性质在时空域中并不完全保持一致，例如在时间轴上信息是有明确的过去、现在和未来顺序的，这种特征在空间域上并不存在，但是时空域却继承了这种时空特性。

　　3.1时空序列的分段

　　本文采用一种基于转折点的PLR方法（CPPLR）进行时空序列的分段。首先通过搜索原始时空序列X={x1,x2,…xn}中的转折点，并将这些转折点用直线段连接起来,就得到了时空序列的一种分段线性表示，获得分段后的时空序列转折点的集合为S={xt1,xt2,…，xtN}，N为转折点的数量，tN=n，终点默认为转折点。CP-PLR方法能有效地发现原始序列中形态变化明显的关键点，识别并剔除序列中的噪声干扰，能有效地压缩数据,并保持较小的拟合误差。

　　时空序列数据聚类分析过程中,不仅需要考虑时空序列的空间邻近性，而且需要考虑在时间上体现的相似性。针对时空序列所具有时空相关性，为很好地对时空序列进行聚类，本文采用基于时空密度聚类中的STDBSCAN算法［8］。

　　时空密度聚类是空间密度聚类在时空域上的扩展，其采用密度作为实体间相似性的度量标准，将时空簇视为一系列被低密度区域（噪声）分割的高密度连通区域。2006年，Wang等人在DBSCAN算法［9］的基础上进一步考虑了时间维，发展了一种基于密度的时空聚类方法STDBSCAN，针对STDBSCAN算法需要过多输入参数的缺点，参考文献［10］中给出了经验设置方法。

　　3.2时空序列的聚类方法

　　STDBSCAN算法可以解决空间属性、非空间属性和时间属性的聚类问题。本文对分段后的数据集合S进行聚类，即当空间内的两个点同时满足空间邻近性与时间邻近性两个要求时则将两点归为一类［11］。聚类后的数据就可以用来建立隐马尔可夫模型。聚类公式为：

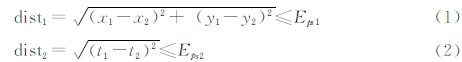
　　Eps1表示空间属性半径,Eps2表示非空间属性半径。存在两个点M(x1,y1,t1)和N(x2,y2,t2)，其中x,y代表空间属性，t代表非空间属性。当M和N同时满足式(1)和式(2)时，M和N点为Eps邻近。

　　3.3基于时空密度聚类的隐马尔科夫模型

　　隐马尔可夫模型 ［12］是以马尔科夫链为基础演化而来。模型可以表示为λ=(A,B,π)，其中状态转移概率矩阵A={aij}，aij表示t时刻从状态Si转移到状态Sj的概率；根据节点采集的原始数据计算出可观察符号的概率分布矩阵B={bik}；初始状态概率πi=P(q1=si)，它表示在初始时刻选择某个状态的概率。隐马尔科夫模型的基本组成如图3所示。

　　一个确定的隐马尔科夫模型可以产生观测序列O={o1,o2,…，oT}，ot表示在t时状态为Si的观察值。那么在隐马尔科夫模型和隐藏状态序列已知的情况下，隐藏状态序列和可观察状态序列O的联合概率为：

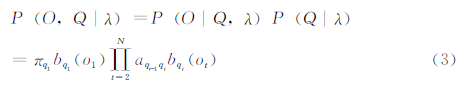
　　其中，P(O，Q|λ)为观察序列O的概率，P(Q|λ)为隐藏状态序列在此隐马尔科夫模型下的概率。由于式（3）在隐马尔科夫模型计算中计算量非常大，所以本文采用后向算法来解决概率计算的问题。根据以上两步确定的隐马尔科夫模型λ，定义在时刻t且状态为qi的前提下，从t+1到T的部分观测序列Ot+1,Ot+2,…,OT的概率为后向概率，记作：βt(i)=P(Ot+1，Ot+2,…,OT|st=qi,λ)，最终的概率公式为：

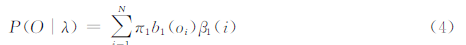
　　本文采用隐马尔科夫模型作为对时空序列进行预测的系统模型，通过聚类算法处理时空序列获得几个隐含状态，从而将时空序列预测问题转化为状态预测问题。

　　通过聚类算法聚类S序列，并将聚类看作K个隐状态，基于时空密度聚类就可以建立状态转移矩阵A。同时以分段后的序列S作为观测对象建立隐马尔科夫模型，由式（4）产生预测序列的概率。

　　最后采用维特比算法预测最优的状态序列：

　　输入：隐马尔科夫模型λ=（A,B,π）和观测序列S=xt1,xt2,…,xtN；输出：最优状态序列S*=x*t1,x*t2,…，x*tN。

4实验验证

　　利用基于密度聚类的隐马尔科夫模型对药品冷藏库内的温度进行预测，采用均方根误差来衡量模型预测的精度，并且对同一个时空序列采用时空神经网络(STANN)、地理加权回归(GWR)分别对其进行下一时刻温度的预测，实验中每隔15 min预测一次，然后计算均方根误差的值，最后将三个模型的误差值进行比较。衡量预测精度的均方根误差公式为：

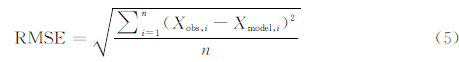
　　其中，Xmodel,i为下一时刻温度的观测值，Xobs,i为模型的预测值，n为预测的次数，均方根误差的值越小说明预测精度越高。图4为基于时空密度的隐马尔科夫模型对药品冷藏库内温度预测方法与STANN模型、GWR方法预测误差值的比较曲线图。

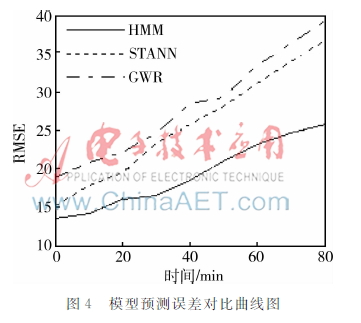
　　从图4中可以看出，本文提出的基于时空密度聚类的隐马尔科夫模型对时空序列的预测具有较高的精度，在进行多步预测之后，误差增长较小，而其他两种模型的预测精度要远低于基于时空密度聚类的隐马尔科夫模型对时空序列的预测，而且随着预测步数的增长，预测误差也越来越大。

5结束语

　　在隐马尔科夫预测模型的基础上，针对时空序列不同于时间序列的特性，本文提出了基于时空密度聚类的隐马尔科夫模型。首先根据时空密度聚类出隐马尔科夫模型所需的隐状态，然后采用隐马尔科夫模型对隐状态序列进行预测。经实验验证，该模型能够很好地预测时空序列，而且由于在处理原始时空序列的过程中能去除其中的噪声，因此预测精度较高。

参考文献

　　［1］ 章登义,欧阳黜霏,吴文李.针对时间序列多步预测的聚类隐马尔科夫模型［J］.电子学报,2014（12）:2359-2364.

　　［2］ Cao Liying, San Xiaohui, Zhao Yueling,et al. The application of the spatiotemporal data mining algorithm in maize yield prediction［J］. Mathematical and Computer Modelling,2013,7(1):507-513.

　　［3］ 王佳璆.时空序列数据分析和建模［D］.广州：中山大学,2008.

　　［4］ 刘美玲.时空地理加权回归模型的统计诊断［D］.西安：西安建筑科技大学,2013.

　　［5］ STRAUSS C, ROSA M B, STEPHANY S. Spatiotemporal clustering and density estimation of lightning data for the tracking of convective events［J］. Atmospheric Research,2013,8(1):98-102.

　　［6］ 彭子平,张严虎,潘露露.隐马尔科夫模型原理及其重要应用［C］.2008年中国信息技术与应用学术论坛,2008:138-139.

　　［7］ 方如果.基于相似性分析的时间序列数据挖掘算法研究［D］.杭州：浙江大学,2011.

　　［8］ 唐建波,邓敏,刘启亮.时空事件聚类分析方法研究［J］.地理信息世界,2013(1):38-45.