0 引言

    该方法作为解决非线性问题的有效手段得到了全面的关注和研究，它的原理是把输入信号映射到高维的特征空间中，在高维的特征空间里再进行线性运算^[1]，从而解决非线性问题。核方法不需要知道映射的具体形式，只需要确定变换后内积的核函数的形式。基于最小均方误差（LMS）算法的核最小均方误差（KLMS）算法已经被证明能够在有高斯噪声的环境下很好地解决非线性问题^[2]，而在实际应用中往往会存在着非高斯冲击噪声^[3]，因而KLMS算法的性能会受到很大的影响。在线性算法中，用对数作为代价函数的最小对数绝对差（LLAD）算法被用来解决这种存在非高斯噪声的问题^[4]。文献[4]中的实验结果表明， 最小对数绝对差（LLAD）算法和传统的最小均方误差（LMS）算法相比，前者具有很好的抗冲击干扰能力，但是LLAD算法仅仅适用于线性系统。本文将LLAD算法引入到核空间中，提出核最小对数绝对差（KLLAD）算法，以此来解决存在非高斯噪声的非线性问题，由于KLLAD算法以对数作为代价函数，能够降低测量误差e(i)对算法更新的影响，所以它在鲁棒性和收敛方面都有很好的表现。

1 KLMS和LLAD自适应滤波算法

1.1 KLMS算法

    Mercer核是一个连续、对称、正定的核函数κ：R^m×R^m→R^[5]，常用的核函数包括高斯核和多项式核，本文使用的高斯核定义如下：

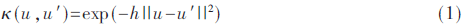
    其中h是核参数，根据Mercer的理论研究，任何核函数κ(u，u′)都可以通过映射φ以内积的形式把输入空间U映射到高维特征空间F（内积空间）中^[6]，其数学表达式如下 ：

    如果定义φ(u)=κ(u，·)，则特征中空间F本质上也是一个核再生希伯特空间，KLMS算法实质上就是在特征空间F中的线性LMS算法^[2]。首先，通过映射φ将输入信号u(i)映射到特征空间F中后变成φ(u(i))，定义φ(i)=φ(u(i))，然后对新的输入数列{φ(i)，d(i)}应用LMS算法可以得到：

    其中，e(i)是第i次的预测误差，η是步长，w(i)是对特征空间中对自适应滤波器抽头矢量的估计。由式(3)可以看出，KLMS算法本质上是在高纬特征空间中的线性LMS算法，是解决非线性问题的有效手段，有着非常广泛的应用。

1.2 LLAD算法

    在传统的LMS算法中，定义输入信号为u(i)，期望输出为d(i)，滤波器输出为y(i)，误差信号e(i)=d(i)-y(i)=d(i)-w(i)^Tu(i)，w(i)是自适应滤波器的抽头系数矢量，最常见的代价函数是E(e(i)²)，通过减少代价函数来逼近待辨识的系统，而在LLAD算法中应用对数作为代价函数^[4]：

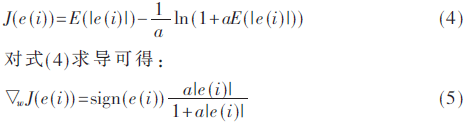
    当式（5）=0时，代价函数便取得最优解，其中a为设计的参数且a>0，因此LLAD算法的自适应滤波器的抽头矢量更新表达式变为：

其中μ为步长参数。

    分析式(6)可知，当e(i)很大时算法更新近似于符号（SA）算法，当e(i)很小时，算法更新近似于传统的LMS算法。因此LLAD算法综合了LMS和SA两种算法^[4]，与LMS算法相比具有很好的抗冲击噪声性能，与SA算法相比具有更好的收敛性能。

2 KLLAD自适应滤波算法

    最小对数绝对差（LLAD）算法虽然具有很好的抗冲击噪声性能和收敛性能，但其只适用于线性系统，并不能直接用来解决非线性问题，因此本文在LLAD算法的基础上提出KLLAD算法，在核空间中应用LLAD算法，把LLAD算法推广到核空间来解决非线性问题，并用系统辨识来验证其鲁棒性和收敛性能。

    首先，通过映射φ将输入信号u(i)映射到特征空间F中后变成φ(u(i))，定义φ(i)=φ(u(i))，然后对新的输入数列{φ(i)，d(i)}应用LLAD算法可以得到KLLAD算法，KLLAD算法第i次的预测误差:

    由式(4)可以得出KLLAD算法的代价函数为：

    如果或者 F(e(i))=0，则对数代价函数可以取得最优解，所以对数代价函数 J(e(i))的最优解与代价函数 F(e(i))的最优解是一致的^[4]。由于 F(e(i))=E(|e(i)|)，利用式(6)可以得出：

    综上所述，KLLAD算法本质上是在特征空间中的LLAD算法，所以其具有LLAD算法的鲁棒性。

3 实验仿真结果分析

    系统辨识是自适应滤波器的一个重要应用，本文用非线性系统辨识来验证KLLAD算法的性能，定义系统噪声由高斯噪声和非高斯冲击噪声线性组合而成，系统噪声混入期望信号对期望信号产生干扰，实验中分别用KLLAD、KLMS和LLAD三种算法来对该未知系统进行逼近，并对比三种算法的鲁棒性和收敛性。

    非线性系统由一个线性信道和一个非线性信道组合而成^[7]，其中线性信道选择为：H(z)=1+0.2z^-1，非线性信道为：y=x-0.9x²，其中x为线性信道的输出。定义非高斯冲击噪声表示为K_i A_i，K_i是一个伯努利过程且p(K_i=1)=p_r，A_i是零均值的高斯过程，系统噪声n(i)由一个方差为σ²的白高斯噪声和冲击噪声K_i A_i组成^[8，9]，在实验中KLLAD算法的参数设定为：核参数h=0.1，σ²=0.4，a=5^[4]，μ=0.1；KLMS算法中σ²=0.4，μ=0.05；LLAD算法中σ²=0.4，μ=0.01。三种算法的训练数据是1 000，测试数据是100，学习曲线取计算30次的平均值。三种算法的性能对比如图1、图2和图3所示。其中图1是没有非高斯冲击噪声的环境，即p_r=0；图2是存在5%的非高斯冲击噪声的情况（p_r=0.05，A_i=150）；图3是存在很大单点非高斯冲击噪声的情况（A₅₀₀=1 500）。

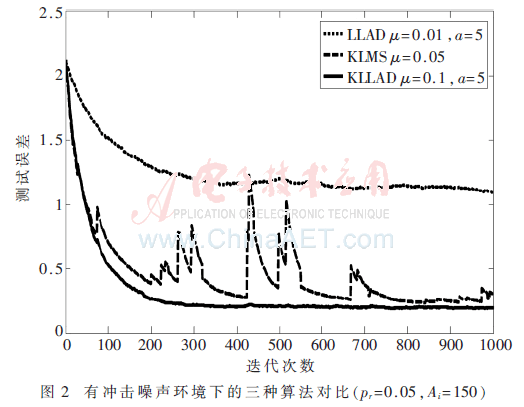
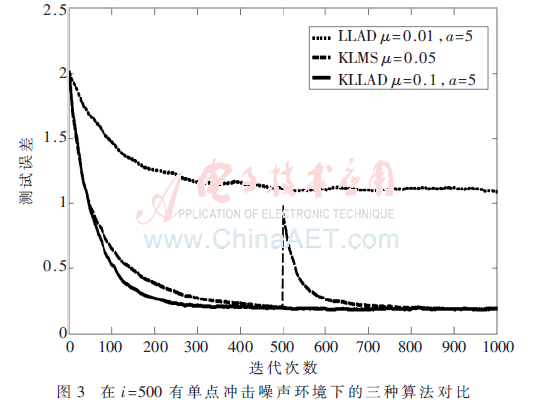
    从图1可以看出：在没有冲击噪声的环境下，KLLAD（μ=0.1）算法和KLMS算法（μ=0.05）具有相近的稳态误差，而且KLLAD算法收敛速度比KLMS要快；与LLAD算法（μ=0.01）相比，KLLAD算法的稳态误差要远远低于LLAD算法，由此也证明了LLAD算法不适用于非线性系统，表明了提出KLLAD算法的必要性。从图2可以看出：在存在非高斯冲击噪声的环境里，KLLAD算法与LLAD都有很好的鲁棒性，能够避免冲击噪声对算法更新迭代的影响，使算法具有稳定性；但是KLMS算法由于受到系统非高斯冲击噪声的影响，稳态误差波动较大，其收敛性能大大降低，KLLAD算法要优于KLMS算法。图3是在第500次迭代时出现一个很大的非高斯冲击噪声，从图中可以看出：在500次迭代时该冲击噪声对KLLAD和LLAD算法并无影响，而KLMS算法在i=500时出现了较大的波动，产生了较大的误差，在非高斯冲击噪声消失后，KLMS算法又会收敛于一个较低的稳态误差，其结果更进一步验证了KLLAD算法的鲁棒性和KLMS算法的局限性，在有非高斯冲击的环境下KLLAD算法要远远优于KLMS算法。

4 结论

    本文提出的核最小对数绝对差（KLLAD）算法是将最小绝对差(LLAD)算法与核方法相结合而形成的新的算法，由于KLLAD算法使用对数作为代价函数，有效降低了测量误差e(i)对算法更新迭代的影响^[4]，使算法更具稳定性，以此来解决存在非高斯冲击噪声的非线性问题，从系统辨识的实验仿真结果来看，在存在非高斯冲击噪声的环境里KLLAD算法与LLAD算法、KLMS算法相比，前者确实具有很好的鲁棒性和收敛性能。

参考文献

[1] LIU W，PRINCIPLE J C，HAYKIN S.Kernel adaptive filtering：a comprehensive introdtion[M].Hoboken，NJ，USA：Wiley，2010.

[2] LIU W，POKHAREL P P，PRINCIPLE J C.The kernel least-mean-square algorithm[J].IEEE Trans.Signal Process.，2008，56（2）：543-554.

[3] CHAMBERS J，AVLONITIS A.A robust mixed-norm adaptive filter algorithm[J].IEEE Signal Process.，1997，4(2)：46-48.

[4] SAYIN M O，VANLI N D，KOZAT S S.A novel family of adaptive filtering based on logarithmic cost[J].IEEE Trans.Signal Process.，2014，62(17)：4411-4424.

[5] ARONSZAJN N.Theory of reproducing kernels[J].Trans.Amer.Math，Soc.，1950，68(3)：337-404.

[6] BURGES C J C.A tutorial on support vecter machines for patten recognition[J].Data Min.Knowl.Disc.，1998，2(2)：121-167.

[7] MIAO Q Y，LI C G.Kernel least-mean mixed-norm algorithm[C].ACAI.Xiamen：IET，2012：1285-1288.

[8] TANRIKULU O，CHANBERS J A.Convergence and steadystate properties of the least-mean mixed-norm(LMMN) adaptive algorithm[J].Proc.IEE-Vis.，Image & Signal Process.，1996，143(3)：137-142.

[9] WALACH E，WIDROW B.The least mean fourth(LMF) adaptive algorithm and its family[J].IEEE Trans.Inform.Theory，1984，30(2)：275-283.