何旭1，杨韵怡1，林怡阳1，邹志强2,3，沈澍2,3

　　（1.南京邮电大学 贝尔英才学院，江苏 南京 210046；2.南京邮电大学 计算机学院，江苏 南京 210003；3.江苏省无线传感网高技术研究重点实验室，江苏 南京 210003）

       摘要：提出了一种基于压缩感知和双簇头交替的无线传感器网络分层路由算法CS-DC HA(Compressed Sensing-Double Cluster Head Alternation)。该算法对DCHS(Deterministic Clusterhead Selection)算法进行改进，利用压缩感知理论优化稀疏采样过程；采用双簇头交替方法进行路由选择，进而实现减低能耗；同时以贝叶斯算法进行稀疏信号重构。通过实验可以看出，相比于传统的无线传感器监测网络，CS-DCHA算法保证了在一定的信号重构精度条件下，能降低无线传感器网络的能耗并延长其生存时间。

　　关键词：无线传感器网络;分簇路由算法;压缩感知;贝叶斯恢复算法

0引言

　　无线传感器网络（Wireless Sensor Networks,WSNs）是集信息采集、传输、处理于一体的综合系统［1］。近年来，WSNs应用于许多领域，尤其是环境监测方面，如水域和森林地理信息采集、污染监测等方向［23］。

　　监测任务通常持续时间长且使用区域特殊，节点供能困难，故WSNs生命周期一般较短。而在工作过程中，数据通信耗能约占总耗能的90%［4］。因此，可从减少数据通信和能耗均匀分布两方面考虑WSNs路由算法的设计。

　　WSNs规模较大时，分簇路由能有效降低通信耗能［5］。DCHS作为一种分簇路由协议，兼顾了簇头选举和数据传输两个阶段的能量均衡问题［5］。但在选簇头和建簇过程中，簇头耗能较高，此时簇头已未必适合继续担任簇头，所以簇头选举时重新选出主副簇头，在数据传输阶段实现双簇头交替［6］（Double Cluster Head Alternation,DCHA）。

　　采样过程中，有些测量值（如水温和气压）在长时间大范围内才会变化，即能够进行稀疏表示。经稀疏表示后，节点所需的采样频率显著降低，从而降低能耗。近年来由美国科学院院士DONOHO D等人提出的压缩感知(Compressed sensing,CS)理论［7］很好地符合这一点。CS要求观测的数据只是原始信号的一个很小子集，可减少采样次数，降低系统能耗［8］。

　　针对监测对象存在时空稀疏性的WSNs，本文首先分析了CS理论用于WSNs采样压缩的过程；接着从减少数据通信量角度出发，给出了能量受限的WSNs应用CS理论采样的系统模型，提出相应的观测矩阵；最后，从能量均衡方面考虑，使用DCHS确保簇头能量充足，在此基础上采用DCHA方法，进一步降低簇头耗能，延长整个WSNs的生命周期。

1压缩感知理论

　　1.1基本原理

　　在标准CS框架中［7］，观测到的自然界的物理信号记为x∈RN，且在某个变换基上有稀疏表示即：

　　x=Ψα，αl0=K，KN(1)

　　其中，α为稀疏变换系数；K为变换系数中非零元个数。在实验中，采用离散余弦变换(Discrete Cosine Transform, DCT)来稀疏原始信号。

　　下面对信号进行某种随机采样，使得

　　y=Φx=ΦΨα，y∈RN，Φ∈RM×N(2)

　　其中，y为随机采样的线性测量值；Φ为观测矩阵；A=ΦΨ为感知矩阵。

　　根据y恢复出稀疏系数的估计值α。通用的恢复方法表达式为：

　　α=argminααl0，s.t.y=ΦΨα(3)

　　一般而言，l0问题（0-范数）属于NP-hard问题，目前很难由多项式法求解。有研究表明，可以把求解l0转化为求解l1,从而转化为线性规划问题［8］，再用多项式法求解，即

　　α=argminααl1，s.t.y=ΦΨα(4)

　　通过求解l1，得到与原问题相同的解。求出α后，再对α进行逆变换，即x=Ψα，从而得到最终的信号估计值。

　　CS的核心思想：以原始信号的可稀疏性，通过变换空间来描述信号。只需采集少数特殊的线性观测数据，通过求解一个优化问题从少量观测数据中恢复信号。传统编解码理论的框图如图1所示，CS理论的编解码框图如图2［9］所示。　

　　图1、图2反映了两者的区别。传统方法按照Nyquist采样定理完成采样后，再进行压缩编码，故CS采样得到的压缩数据的数据量远小于传统采样，大大降低了采样和通信的耗能。

　　1.2构建观测矩阵

　　CS主要由信号的稀疏表示、观测矩阵和重构算法构成。其中，建立观测矩阵是关键过程［10］。

　　DONOHO D提出了相关性判别理论: 观测矩阵Φ与稀疏基Ψ的不相干程度越高，稀疏信号的精确重构所需的观测数越少。DCHS结合CS后，簇的数量取决于观测向量的行数［11］，应为μ2klogN，即：簇头百分比为p=klogNN。其中，k为信号的稀疏度，N为局域内节点的个数,μ2为稀疏矩阵和观测矩阵的相干性。

　　CS常采用随机观测矩阵，这类矩阵元素往往独立同分布。测量矩阵和稀疏信号大多不相干，需重建的测量数小，但所需存储空间大且计算复杂度高。一般的分簇路由算法存在簇头通信和处理负担过重的缺点。因此，提出CS-DCHA，采用DCHS分簇,然后构造CS观测矩阵，系统模型如图3所示。其中，所有节点依据地理信息和通信距离划分簇。观测矩阵由各簇的观测向量组成，每簇的观测向量仅在本簇节点位置处非零。

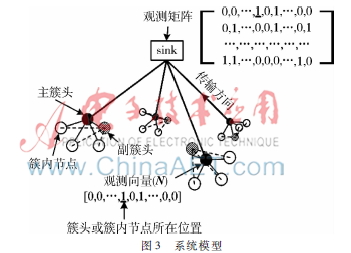
　　观测向量仅在簇头上存储，每簇的节点数也相对较少，对存储空间和计算复杂度的要求有所降低。

　　建立观测矩阵的具体过程如下［12］：在观测向量中本簇节点位置处置1，表示该节点属于当前簇。簇头封装观测向量与数据，一同发送给sink节点。sink节点从所有簇头中提取数据和观测向量，并将所有观测向量组合在一起形成观测矩阵Φ∈RM×N，其中Mμ2klogN［13］。这就是一“轮”中观测矩阵的建立过程。重复执行上述步骤，并形成新的观测矩阵。

2CS-DCHA算法

　　CS-DCHA算法主要包含两个阶段：成簇阶段和稳定阶段。成簇阶段又可分为选举簇头与形成簇；稳定阶段是WSNs正常工作阶段，此阶段采用双簇头交替。

　　2.1CS-DCHA算法的成簇阶段

　　在选簇头时，每个节点产生一个0~1随机数，若该随机数小于阈值，则该节点选为簇头。

　　阈值的计算公式为：

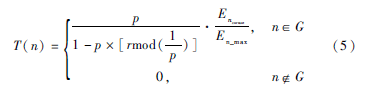
　　其中，p为簇头占节点总数的比例；r为目前的轮次；rmod(1/p)为本轮循环中当选过簇头的节点个数；Encurrent为节点当前能量；En_max为节点初始能量；G为在近1/p轮中未担任簇头的节点集合。在选举簇头时，将能耗比例较低的节点优先选为簇头。

　　簇形成时，要考虑两点要素：簇头间的负载平衡和簇能量消耗总和最小。节点当选簇头后，全域广播该消息，其他节点接收到由多个簇头广播的消息，分别计算到这些临时簇头的距离，加入通信代价最小的簇头所在网络，向当前簇头发送剩余能量与地理位置等信息，从而形成簇。

　　选举簇头与形成簇的效果如图4所示。sink节点、簇头、簇内节点构成一个两跳网络。sink节点负责全局的数据融合；簇头负责区域内的数据转发和计算处理；簇内节点负责信息感知。

　　WSNs能耗模型采用自由空间模型与多径衰减模型［6］。当通信距离大于阈值d0，发送数据所需能量正比于距离的4次方，反之正比于距离的平方。发送方发送k bit数据消耗的能量由发射电路损耗与功率放大损耗两个部分构成，可表示为

　　ET（i）=kEelec+kεfsd2,d<d0

　　kEelec+kεmpd4,d≥d0（6）

　　接收k bit数据所需的能量为：

　　ER(i)=kEelec(7)

　　其中，Eelec是收发单位数据消耗的能量，而阈值为：

　　其中，εfs和εmp是两种情况下功率放大器消耗的能量比例系数。

　　2.2CS-DCHA算法的稳定阶段

　　在稳定阶段，首先解决双簇头选举问题。在簇形成后，重选主、副簇头。

　　在成簇过程中，原簇头已获得所有成员节点相关信息，用集中式算法来选举簇头。计算节点竞争力［6］:

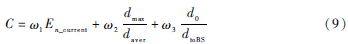
　　定义簇头选举的能量阈值Eelect为发送和接收50个数据包的能量消耗，若节点能量小于Eelect，则不参加竞选。定义簇内备选节点的竞争力为C;En_current为备选节点的剩余能量;dmax为备选节点到簇内其他节点的最大距离;daver为备选节点到簇内其他节点的平均距离,计算公式如式（11）所示；dtoBS为备选节点到基站的距离；d0为无线通信能耗模型中的距离阈值；ω1、ω2、ω3为权重系数，且：

　　其中，dto_node_i为备选节点到簇内第i个节点的距离，N为簇内节点总数。

　　则新的簇头选举公式为：

　　I=max0<i<N（Ci）(12)

　　求解出式(12)的最优解与次优解。

　　选举簇头时，备选节点距基站越近、剩余能量越大、到其他节点的平均距离越小，其竞争力越强。原簇头遍历所有成员节点，选取C值最大和次大的节点为主、副簇头。

　　选举结果如图5所示。与图4不同的是，在这个两跳网络中，黄、绿线分别代表主、副簇头交替与sink节点通信，而簇内部结构不变。

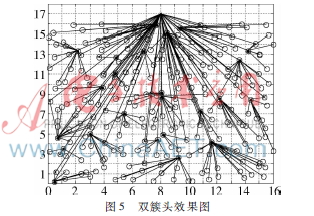
　　在稳定阶段的交替机制中，对Nslot个时隙周期进行操作。时隙周期总数由式（13）求得［6］：

　　其中，T为每轮数据传输阶段的时间，Tslot为时隙周期。设m个时隙周期为一组，将Nslot个时隙周期分为H组，且

　　当H为奇数时，主簇头工作，副簇头退化为普通节点；当H是偶数时，反之。如此交替，节点将数据发送到当值簇头，簇头将数据发送给sink节点，大幅推迟簇头的死亡时间。

　　式（14）中，m为唤醒因子。若m为1，则主副簇头轮换频繁，会耗费额外能量用于通信模块的频繁唤醒；若m太大，副簇头工作时主簇头需要较长的睡眠时间，主簇头对簇的动态管理(如更换簇头、新节点加入等) 会受到影响。因此，应根据实际情况来灵活设置m值。

　　综上所述，CSDCHA的算法流程如下：

　　CSDCHA在成簇后，以主副簇头的剩余能量为迭代的循环条件，存活节点数为迭代的终止条件，循环完成双簇头选举、交替采样传输的工作。

3仿真结果

　　本文使用MATLAB对CSDCHA进行验证。仿真场景为：N=256个传感器节点均匀分布在160 m×160 m的正方形区域内，基站位于区域外，坐标为(80，170)。CS理论和分层路由结合，观测矩阵的维数M≥4k［8］，假设k=10，则成为簇头的最佳比例p≈0.15。仿真结束条件为存活节点数小于满足CS采样的最低需求。

　　仿真过程中，实现了数据处理、簇的划分、簇头选举、观测矩阵建立与数据传输以及数据压缩与恢复的全过程。其中，重点观察节点的生命周期和恢复精度。

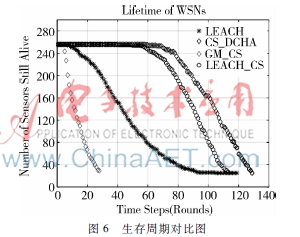
　　生存周期方面，将CSDCHA、经典LEACH、CS结合LEACH（记为LEACH_CS）以及CS结合高斯随机矩阵（记为GM_CS）进行对比，如图6所示。由图6可看出：GM_CS很快就有大量节点死亡，说明了采用分簇路由算法的必要性；LEACH_CS和LEACH相比，节点的生存时间有了很大的提升，说明CS在节省耗能方面的优越性；CS-DCHA和LEACH_CS相比，在第一个节点死亡时间上更有优势，这是因为在分簇的基础上，采用双簇头轮换传输，能量消耗更为分散，耗能更均匀。

　　恢复方面，采用BCS算法［8］。对稀疏系数进行BCS估计，求出原始信号的估计值，部分恢复结果如图7所示。经测算，误差率为0.003 8，恢复时间为0.045 s，误差在允许范围内。　

4结论

　　本文提出了一种基于双簇头交替和CS理论的WSNs路由算法——CSDCHA算法，CSDCHA可以提高WSNs网络的生命周期，并降低能量损耗。仿真结果证明了算法的可行性和有效性，且在网络生命周期方面优于经典的LEACH路由算法和采用高斯随机矩阵的CS方法。但该算法还存在一些不足，如分簇的过程中没有考虑簇的大小均匀分布；观测矩阵仅实现了从簇头传输到sink节点数据的稀疏表示，簇内采集数据过程并未应用CS理论。这些问题都需继续研究。

参考文献

　　［1］ 李建中，高宏. 无线传感器网络的研究进展［J］.计算机研究与发展,2008,45(1):115.

　　［2］  Liu Yunhao, He Yuan, Li Mo, et al. Does wireless sensor network scale? A measurement study on GreenOrbs［J］. IEEE Transactions on Parallel Distributed Systems,2013,24(10):19831993.

　　［3］ 胡娇,孙坚,王晓薇,等.基于WSNs水环境云端监测系统研究［J］.微型机与应用,2015,34 (11):6063.

　　［4］ 王泉,张纳温,张金成.压缩感知在无线传感器网络数据采集中的应用［J］.传感技术学报,2014,27(11):15621567.