0 引言

    在脑机接口中，人们在想象单侧手运动时，对侧相应初级感觉运动皮层区的脑电信号幅值降低，这种现象称为事件相关去同步(Event-Related Desynchronization，ERD)；同侧脑电信号幅值升高，称为事件相关同步(Event-Related Synchronization，ERS)^[1]。研究表明，在想象左/右手运动时，大脑感觉皮层的μ节律和β节律出现一定变化，并遵循ERD/ERS规律。为此，利用ERD/ERS现象进行脑电信号的特征提取与分类成为BCI研究的关键环节。

    在特征提取方面，LMD是一种新的自适应非平稳信号处理方法，能够从原始信号中分离出纯调频信号和包络信号，将其相乘便可以得到具有瞬时物理意义的PF分量^[2]。目前，很多学者对基于LMD的运动想象信号进行了研究。但是该方法在应用时存在端点效应问题，使得信号产生畸变，分解过程中可能会造成信号两端端点发散，导致信号在重构时丢失部分原有特征^[3]。为了降低这种端点效应的影响，本文采用改进LMD算法进行特征提取。

    改进LMD分解后的PF分量依次是高频到低频的时间序列，而样本熵能衡量时间序列中产生新模式概率的大小，具有较好的抗噪和抗干扰能力，对丢失数据不敏感^[4]。故用样本熵对PF分量进行量化，可提高特征提取准确率。

1 改进的LMD算法

1.1 算法介绍

    本文利用相似波形加权平均的端点延拓法来改善其端点效应的影响，以左端点为例，设原始信号为x(t)，具体算法如下^[5]：

    (1)x(t₀)为起点，向右取x(t)的曲线段，长度为w(t)，并有且有一个极值点和一个过零点；

    (2)设w(t)右端点是过零点，记为x(t_n)，则其中间点 x(t_m)=(x(t₀)+x(t_n))/2。以x(t_m)为参考点，沿时间轴t向右平移子波w(t)，若存在某一点x(t_i)与x(t_m)重合时，取以x(t_i)为中点并与w(t)等长子波，记为w_i(t)。计算w_i(t)与w(t)的波形匹配度m_i，并存储该波形匹配度m_i与w_i(t)的前一小段数据波（取其长度为0.1 l），将这些长度为0.1 l的左邻数据波记为v₁(t)，v₂(t)，…，v_k(t)，并得到如下数据对集合[v，m]={(v(t)，m)|(v1(t)，m₁)，(v₂(t)，m₂)…(v_k(t)，m_k)}：

    (3)当集合[v，m]为空时，表明原始信号波形不规则，不进行延拓，转步骤(5)；

    (4)当集合[v，m]不空时，将求得的波形匹配度按降序排列，得到 [v′，m′]。计算[v′，m′]中前n个数据对所有子波的加权平均值，得到平均波 v_a，并用v_a延拓信号左端点；

    (5)延拓结束。

    同理可对信号右端点进行延拓。

1.2 PF分量选择

    目前研究表明，人在想象左/右手运动时，其大脑运动感觉皮层的μ节律(8～12 Hz)和β节律(14～25 Hz)会出现一定变化^[6]。脑电信号经过改进LMD分解成一系列PF分量之和，选出包含特征频率多的PF分量作为分类输入信号，以此提高特征提取的效率和精度。本文通过以下方法选出包含大部分μ节律和β节律的PF分量，具体步骤如下：

    (1)通过改进LMD方法将脑电信号分解为PF分量和，求取各个PF分量对应的瞬时频率F(t，f)，然后计算各个PF分量中8～25 Hz频带能量，如式(1)所示。

其中F₁，F₂为所取频率的上下限，即分别为8 Hz和25 Hz；T₁，T₂为所取得特征时间的上下限；i=1，2，…，N，N为信号分解的PF分量个数。

    (2)根据式(1)中结果，求取各个分量中8～25 Hz频带能量所占总能量的比例，得出该频段能量的分布情况，最后选出该频段能量分布较多的PF分量：

1.3 特征时间段选择

    在运动想象信号研究中，其ERD/ERS现象不能持续贯穿于整个信号时长，如果把整个时长的运动想象信号都作为研究对象，可能会包含许多噪声信息，影响提取效率和精度。故本文通过选取特征频段能量差异最大的时间段，找出ERD/ERS现象明显的运动想象信号，具体步骤如下：

    (1)将C3，C4导联的运动想象信号分别经过改进LMD算法分解，得到两组PF分量和；

    (2)用1.2节中介绍的方法选出特征频段所占比例较大的PF分量，并计算选取分量的瞬时频率；

    (3)计算所选取PF分量中滑动时间窗口长度为m秒的特征频段8～25 Hz能量，并规定滑动步长为n秒。

    (4)计算C3，C4对应时间窗内的能量差，将能量差最大时所对应的时间段作为本文特征选择最佳时间段。

2 样本熵

    设时间序列为x(1)，x(2)，…，x(N)，样本熵具体计算过程如下^[7]：

    (1)将上述序列按顺序组成m维矢量：

3 SVM分类

    将左右手想象运动识别看作二分类问题，用支持向量机建立模型。将数据分为训练集和测试集。采用10-fold交叉验证方法进行度量，并求取其分类准确率。

    支持向量机是一种有监督学习算法，该算法首先将特征向量映射到一个高维空间，并在空间中依据训练数据标签分布建立一个超平面集合，再从此集合中选择使得分类间隔最大的一个作为分界面，使得测试数据产生错误分类的概率更小[8]。SVM不但可以提高泛化性能，还可以解决高维和非线性问题，并避免局部极小值。

4 实验分析

4.1 数据介绍

    实验数据来自于BCI 2003竞赛数据^[9]。实验中通过光标移动来模拟左右手运动的思维过程。电极位置和时序图如图1所示。在9 s测试时长中，前2 s试验者处于放松状态，第2 s时系统发出一个声音信号提示试验者测试即将开始。这时显示屏出现一个“+”字，持续1 s。第3 s时，“+”字变为左右箭头，同时要求试验者按照左右箭头的提示想象左右手运动。

    整个实验分为280组，训练数据和测试数据各140组，分为左手和右手两个类别。信号采样频率128 Hz，包含C3、Cz、C4三个导联，Cz为参考导联。

4.2 实验结果

    本实验利用改进LMD算法对脑电信号进行分解，因受试者在第3 s时开始进行想象运动，到第9 s结束，故本文选取3～9 s内不同时间段进行分析。本文以C3 导联作为分析对象， 图2为C3导联在3～9 s想象运动时改进LMD分解示意图，其中X(t)为原始信号。图3为各个PF分量对应的瞬时频率图。

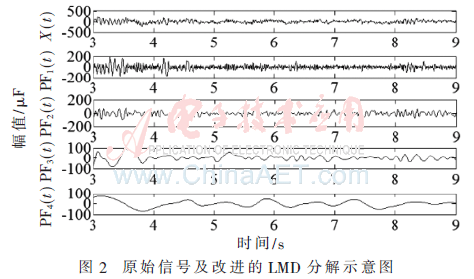
    从图3中可以看出第4个PF分量所包含的频率基本在5 Hz以下，故本文只选取前3个PF分量作为研究对象。随机选取140组左右手想象信号进行改进LMD分解，得到各分量中特征频率（8～25 Hz）所占比，对该140组所占比求平均值，得到特征频率（8～25 Hz）分布情况（见图4）。可知C3、C4导联信号的特征频率成分主要分布在PF2和PF3中，故本文只选取PF2和PF3作为后续特征时间选择的研究对象。在选择最优特征时间段时，采用的滑动时间窗为2 s，滑动步长为1 s，表1为传统LMD和改进LMD特征提取方法在各个时间段的分类结果。

    从表中发现，传统LMD和改进LMD均在4～6 s时间段提取的特征分类效果最好。故实验中选取4～6 s的想象信号作为分类数据。本文以改进LMD算法为例，先将4～6 s脑电信号分为一系列PF分量之和，然后将PF2和PF3的样本熵作为特征向量进行左右手想象运动的识别。图5(a)和图5(b)分别为想象左右手运动的样本熵，从中可知想象左手运动时，C3导联的样本熵值大于C4导联的样本熵值；想象右手运动时， C3导联的样本熵于C4导联。这与ERD/ERS现象完全符合，从而验证了该方法的有效性。

4.3 实验比较

    随机选择140组数据作为训练集，剩余为测试集。按照上述方法，将PF2和PF3的样本熵作为SVM输入特征进行训练，然后对测试集进行测试，最后将改进LMD传统LMD算法进行比较，结果如图6所示，其中a表示传统LMD算法，b表示传统LMD和样本熵，c表示改进LMD，d表示改进LMD和样本熵。

    由图6可知，改进LMD算法比传统LMD识别率提高大约4个百分点，样本熵可以提高分类准确率，改进LMD算法和样本熵的结合使得分类准确率达到最高，进而表明本文方法的可行性。

5 结 论

    本文提出基于改进LMD运动想象信号的判定方法，将PF2和PF3的样本熵作为SVM的输入向量进行识别。通过和传统LMD算法的分类效果进行对比，结果表明本文提出的方法能够有效对左右手运动想象信号进行分类，并获得较高的识别准确率。

参考文献

[1] PFURTSCHELLER G，NEUPER C.Future prospects of ERD/ERS in the context of brain-computer interface(BCI) developments[J].Progress in Brain Research，2006，159(1)：433-437.

[2] SMITH J S.The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society Interface，2006，2(5)：443-54.

[3] 赵娜.HHT经验模式分解的周期延拓方法[J].计算机仿真，2008，25(12)：346-350.

[4] 刘慧，和卫星，陈晓平.生物时间序列的近似熵和样本熵方法比较[J].仪器仪表学报，2004，25(S1)：806-807.

[5] 朱晓军，吕士钦，王延菲，等.改进的LMD算法及其在EEG信号特征提取中的应用[J].太原理工大学学报，2012，43(3)：339-343.

[6] 贡平.运动想象脑电信号特征提取研究[D].重庆：重庆大学，2014.

[7] RICHMAN J S，MOORMAN J R.Physiological time-series analysis using approximate entropy and sample entropy[J].American Journal of Physiology Heart & Circulatory Physiology，2000，278(6)：H2039-H2049.

[8] DURBBA S S，KING R L，YOUNAN N H.Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer[J].Remote Sensing of Environment，2007，107(1)：348-361.

[9] BLANKERTZ B.The BCI Competition 2003：progress and perspectives in detection and discrimination of EEG singletrials[J].IEEE Trans.Biomed.Eng.，2004，51(6)：1044-1051.