洋洋,陈小惠
(南京邮电大学 自动化学院,江苏 南京 210023)
摘要:针对人体血压无创检测问题,提出了一种基于心电信号(Electrocardiogram,ECG)与光电容积脉搏波(Photoplethysmograph,PPG)的血压测量算法。通过脉搏波传递时间(Plusewave Transit Time,PTT)计算出收缩压;将弹性腔模型与脉搏波特征K值模型相结合,计算人体舒张压。实验中,对采集到的心电信号和指尖脉搏信号进行数字滤波,采用自适应特征提取方法对信号波形进行准确地分析计算,实现血压的无创连续监测,且计算结果与标准仪器测量结果相比平均误差小于5 mmHg。
关键词:光电容积脉搏波;脉搏波传导时间;弹性腔模型;特征K值
0引言
血压是人体极为重要的生理参数,分为收缩压和舒张压两部分,能够直观反映出人体心血管功能状态。在临床医学上常用的血压测量方法主要分为有创检测和无创检测[1]。有创血压检测技术主要使用在心脏以及其他重大手术中,优点在于实时性好、准确性高,缺点则是对人体有一定伤害且不适于日常检测。在日常检测中,一般使用无创血压检测技术,常见的方法有动脉张力测定法和脉搏波波速法[2]。动脉张力测定法是根据传感器与动脉血液中的压力成正比,换算得到收缩压和舒张压,虽然换算简单,但是该方法需要借助袖带充气来完成,受外界因素影响较大,无法连续测量。脉搏波波速法则是根据动脉血传递的速度来换算血压,人体的各个部位都能进行检测。与动脉张力法相比,脉搏波波速法测量简便,准确性较高,同时具有对血压进行长时间连续监测的特点,因此该方法具有广泛的应用前景。
本文以波速法为理论基础,前端采集使用型号为HKG07B的光电脉搏传感器和自主研发的心电模块。首先对采集的心电脉搏信号预处理,采用自适应特征提取方法,计算出脉搏波传递时间,推算PTT与收缩压回归分析方程。利用弹性腔模型和脉搏波特征K值准确地计算出舒张压,实现血压的连续无创检测。
1基本原理
1.1信号测量原理
脉搏波波速法等同于测量同一距离内脉搏波传导时间,通常情况下使用一路ECG信号和一路PPG信号来测量。
脏在每个心动周期中,由起搏点、心房、心室相继兴奋伴随着生物电变化,通过心电描记从体表引出多种形式的电位变化图形,得到图1所示心电图。

在进行无创血压测量时,血管中血液容积的变化通过PPG信号来表现。当一束特定波长的光照射到手指上时,光电接收器接收反射或透射的光,接收的光的强弱反映了指端血液成分对光吸收的多少,再对光电脉搏波中的交流成分描记,即可得到如图2所示的PPG信号[3]。

1.2收缩压测量原理
当血压较高时,动脉血管壁相对紧张收缩,使脉搏波传递加快;当血压较低时,动脉血管壁变得松弛,脉搏波传递减慢。脉搏波传递速度与血管弹性之间的关系可以使用莫恩斯科特威公式表示[45]:

其中,v为脉搏波传递速度,g为重力加速度,E为血管壁的弹性模量,a为血管壁厚度,ρ为血流密度,D是平衡状态下血管壁内径。血管壁弹性模量与血管壁压力成指数关系:
E=E0·eγ·Ps(2)
其中,E0是压力为零时的弹性模量,Ps为血管壁压力,将此定义为收缩压,γ为血管特征量[6],数值一般在0.016~0.018 mmHg-1。
脉搏波传导时间是指脉搏波通过动脉树从一点传递到另外一点所用的时间,记为PTT,那么脉搏波的传播速度可以表示为:

式(3)中,S是脉搏波传递的距离。
将式(3)和式(2)代入式(1)中,整理得:
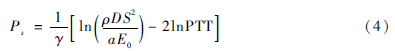
假如忽略血压变化时动脉内径大小和血管壁厚度的改变,式(4)中右边首项可以看成一个常量,再对PTT求导可得:

由式(6)可知,收缩压的变化与脉搏波传递时间PTT呈线性关系,因此也可简写为:
Ps=a·PTT+b(7)
针对同一个被测对象,在一段时间内,a、b的值为常量。本文把ECG信号的R波峰值点作为PTT的起始点,脉搏波的波峰作为PTT的终点(图3所示),通过测量多组PTT值,结合听诊法得到的收缩压进行线性回归就可以标定出a和b,继而实现收缩压的连续测量。

1.3舒张压测量原理
舒张压的测量与收缩压的测量有所不同,舒张压与脉搏波的传递时间并没有明显的线性关系。为了进一步分析舒张压与脉搏波之间的关系,引入血管的弹性腔模型[7],如图4所示。

其中,qin为血液单位时间的流入量,而qout为血液单位时间的流出量,V为血管容积,P为主动脉内的压力, R为血管的外周阻力,C为动脉顺应性。
根据该模型可以得到舒张压和收缩压之间的关系:

式中,Td为脉搏波的下降沿舒张期时间,可以通过脉搏波数据计算得到。则求舒张压的未知量就剩血管外周阻力R和顺应性C。
外周阻力和顺应性的测量需要借助复杂的医疗仪器。为了降低测量成本,本文结合罗志昌[8]等人提出的脉搏特征K值理论,建立外周阻力和顺应性关于特征K值与周期T的关系方程,记为fK,T,则式(8)可表示为:

特征K值与心搏输出量、外周阻力、顺应性等都有密切关系,是心血管疾病检测的一个重要生理指标,因此在临床上有重要的应用价值。根据脉搏波波型面积变化将脉搏波特征量K值定义为:

式中Pm为平均动脉压,其值为一个心动周期中脉搏压力P(t)的平均值,Ps,Pd分别为收缩压和舒张压(图5所示)。
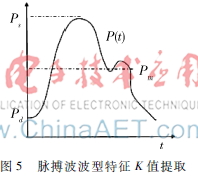
在实际计算中,将PPG信号的波峰作为Ps,波谷作为Pd,周期内信号的平均幅值作为Pm,即可计算出特征值K。通过分析数据发现,被测对象的RC值与KT线性相关,得到fK,T的线性方程:
fK,T=mKT+n(11)
与收缩压的标定方法类似,针对同一个被测对象,在一段时间内,m与n的值为常量。
2信号处理和分析
2.1ECG信号处理
人体的心电信号由一系列的特殊波形组合而成,主要包括P波、QRS波、T波以及以一定概率出现的U波,其中T波出现概率最大且影响最大。为了找到PTT的起始点,即R波波峰位置,需要去除T波干扰。本文采用一阶差分的方法来进行处理[9],具体方法如下:
假设心电信号为数组x(n),对数组x(n)进行差分运算,得到一阶差分数组y1(n):

将原始数组和差分后数组使用MATLAB进行仿真,其效果如图6所示。原始ECG信号经过一阶差分后,基本消除了T波,R波峰值更加明显,便于后续特征点检测。

2.2PPG信号处理
脉搏信号提取时伴随较大的随机性干扰,信号毛刺较多,采用滑动平均滤波的方法可以有效降低干扰对整个脉搏波波型的影响。滑动平均滤波方法相对简单,既可以在消除噪声方面当作低通滤波器使用,又可以起到类似高通滤波器减缓基线漂移的作用。
假设平均点数为m,则平均得到的点y(n)的表达式为:
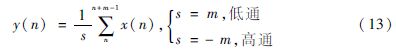
式(13)中,s表示滑动平均系数,n表示数据点的位置,x表示滑动平均前原始数值。
滑动平均点数m的选取与波型峰值间距和采样频率有关,理论上要求满足如下关系:
m=峰值间隔时间/采样周期
但在实际使用中,信号采集频率高,峰值间隔与采样周期比值较大,可能会导致滑动平均点数m过大,细小特征因平滑而消失。为了保证算法的准确性,在实验中只要确保滤波以后的波型在各个波段相对平滑,毛刺噪声较少即可。本文中使用m=4的四点平滑滤波,其滤波效果如图7所示。

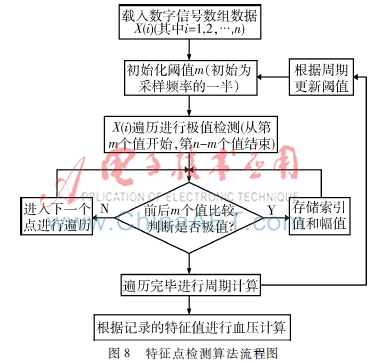
2.3自适应特征点检测算法
得到处理过的信号数据后,需进行特征提取,提取对象主要包括:ECG信号的R波峰值、PPG信号波峰和波谷。其中,ECG信号的R波峰值为周期的极大值,但PPG信号周期内有多个极大值。因此,本文采用一种自适应周期阈值的方法来检测特征点,确保检测出的极值点均为周期内最大值或者最小值,方法流程如图8。
3实验结果与分析
为检验算法的准确性,选4名年龄均为23~30周岁的测试者(分别用A,B,C,D表示)进行测试,测试过程分两步,首先测试得到被测者的各项回归方程系数。在此过程中,分别同步采集20组测试者不同状态下的PPG、ECG数据,计算出PTT、K等参数,采用OMRON电子血压计进行拟合,计算出收缩压的线性方程和被测对象的RC值与KT的线性关系方程。第二步,通过标定数据,对被测对象进行血压连续监测,与电子血压计进行比对,验证其准确性。
图9、图10是以被测者A为例,对收缩压线性拟合和RC与KT相关性拟合示意图。
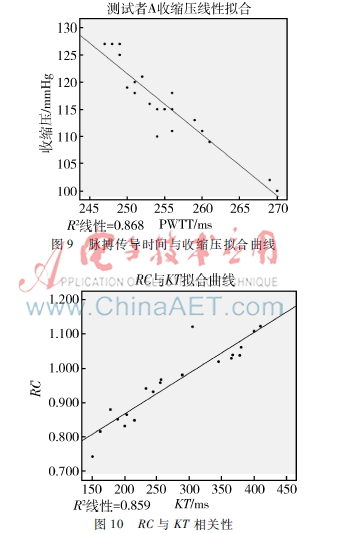
由图9、10可知,对收缩压和脉搏传导时间、RC值与KT进行曲线拟合,其拟合优度R2均大于0.85,说明具有较强的线性关系。因此,可以通过该线性关系,得出测试者相关标定系数,然后展开连续血压监测。
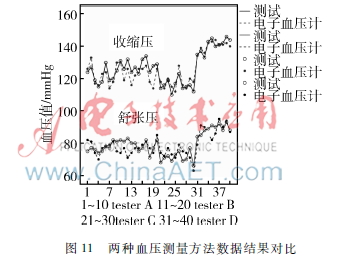
图11展示了A、B、C、D四位测试者采用两种血压测量方法测量各10组数据的对比,从图中可以看出收缩压和舒张压的两条折线整体走势一致,具有很好的一致性。
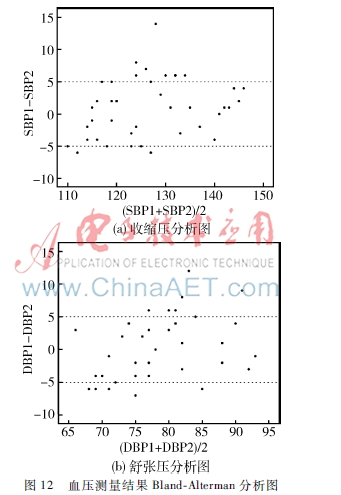
为了更加准确地验证测量方法的一致性,采用BlandAlterman方法[10]来进行验证。验证结果如图12所示,其中横坐标表示测量血压的平均值,纵坐标表示测量血压的差值。上下两条虚线代表5%的相对误差。从图中可以看出,两者之间的血压差值主要集中在±5%这个区域,两者之间的平均差值小于5 mmHg,本文方法与袖带式电子血压计的测量方法具有良好的一致性,可以作为无创连续测量血压的一种。
4结论
本文提出一种利用PPG与ECG信号准确测量血压的算法,该方法采用自适应特征提取两路信号的特征点,利用已有的波速法测量收缩压,将脉搏波的特征K值与弹性腔模型结合测量舒张压,通过与袖带式电子血压计测量结果比对,平均偏差小于美国医疗促进协会建议的5 mmHg,验证了该方法的可行性,为无创连续血压测量提供了新的方法。
参考文献
[1] 廖容,彭锐.无创血压监测方法的研究进展[J].护理学报,2010,17(11):2022.
[2] 凌振宝,张铭,熊文激,等.基于脉搏波传导时间的无袖带血压测量仪设计[J].电子测量与仪器学报,2012,12(10): 10801085.
[3] 李顶立.基于脉搏波的无创连续血压测量方法研究[D].杭州:浙江大学,2008.
[4] ALLEN J.Photoplethysmography and its application inclinical physiological measurement[J].Physiological Measurement, 2007,28(1):139.
[5] 张爱华,王亮. 基于时变图像序列的脉搏信息提取[J].仪器仪表学报,2007,5(11):820825.

