0 引言

    海表面电磁散射问题的研究在微波遥感、环境监测及海上目标识别等领域中有重要意义和价值。以往的研究通常把海面近似为简单的线性模型，但实际海浪的非线性特征会对海面的散射回波产生重要影响。

    目前，国内外很多学者对时变非线性海面的电磁散射问题展开了大量研究。文献[1]将海面高度和潜在的速度矢量表示成一对规范的哈密顿函数，提出了“改进的线性模型”。文献[2]提出了尖波模型，其在海面电磁散射特性的研究中得到了广泛应用。文献[3]提出小斜率近似模型，它构造出满足互易性的幂级数展开式。文献[4]通过引入海浪的二阶谱来反映波面的不对称性，研究了非高斯表面分布的海面的后向散射系数。

    本文在线性海面建模的基础上，引入尖波模型进行修正，得到非线性海浪的形态特征及统计特性。采用小斜率近似法研究了两种海面模型在不同条件下的电磁散射问题并模拟出微波段的回波多普勒谱。结果直观地反映了海面的非线性特征对微波段雷达回波的影响。

1 线性与非线性海面建模

1.1 线性海面建模

    海浪谱反映了海浪的能量在空间频率上的分布，本文采用Pierson-Moskowitz谱，其表达式为：

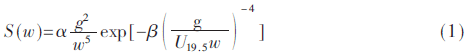
式中，α=8.1×10^-3，β=0.74， w为海浪角频率，U_19.5是海面上方19.5 m处的风速，g为重力加速度。

    根据线性波浪理论，某一时刻的波面位移为一系列不同振幅、频率及初始相位的余弦波的叠加。本文采用双叠加法来建立线性海面模型，可得到波面位移为：

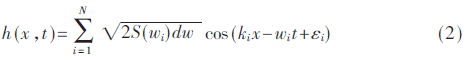
其中， x表示海面离散点的位置， t为时间， N是频率上的离散点数，w_i为角频率，k_i为波数，ε_i取0~2π内分布的随机相位。

1.2 非线性海面建模

    由于海浪的非线性作用，实际海面的形态以及统计参量与简单的线性海面模型不同，而这种非线性特征会对微波段的电磁散射产生重要影响。在各种非线性理论分析中，尖波模型(Choppy Wave Model，CWM)有便于计算的解析形式。该模型对t时刻线性海浪的波面位移进行希尔伯特变换，计算得到海面水平方向位移的增量：

2 电磁散射计算

    小斜率近似方法(Small Slope Approximation，SSA)由VORONOVICH A提出^[5]，其综合了基尔霍夫近似方法和微扰法，适合计算具有复合尺度粗糙度的海面散射问题。故本文采用一阶小斜率近似方法。

    微波段电磁波入射到长度为L的海面z=h(x，t)上，时变海面的散射几何模型如图1所示。入射波矢量为K_i，散射波矢量为K_s，θ_i和θ_s分别为入射角和散射角。

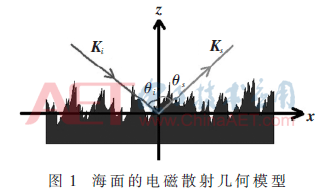
    根据图1中的几何关系，入射波矢量和散射波矢量可表示如下：

式中，k₀和q_i分别为入射波矢量投影到x轴和z轴的分量，k₁和q_s分别为散射波矢量投影到x轴和z轴的分量。

    由于仿真的海面长度有限，可能会在掠入射时产生较强的边缘绕射现象，导致后向散射系数的计算出现偏差。为了消除这种影响，本文采用锥形平面波作为入射场，其表达式如下。其中，k_i为入射电磁波波数，θ_i为入射角，g是锥形波的波束宽度因子。

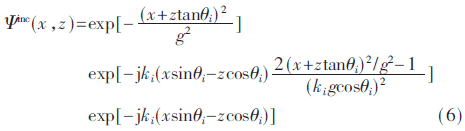
    根据SSA中散射振幅的不变性可以推导得到散射振幅的表达式为：

式中，P^inc为入射波的功率，B(k₀，k)为根据极化方式取值的一阶散射系数矩阵[6]。将海水当作理想导体对其进行简化，得到不同的极化方式可表示如下^[7]。其中，B_vv表示垂直极化方式，B_HH表示水平极化方式。

    多普勒谱可以由散射振幅S(k₀，k₁，t)推导得到：

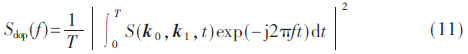
3 数值结果分析

3.1 线性与非线性海面的统计特性对比

    图2表示某一时刻线性和非线性海面的波面位移的对比。U₁₀=10 m/s，海面长度取200 m。取T=0.5 s时刻，横轴是海面的水平距离，纵轴表示波面位移。分析图2可以看出，非线性海浪是波谷相对较平缓而波峰较陡峭的非对称曲线。这与斯托克斯波理论相符合，是非线性海浪的一个重要表现特征。

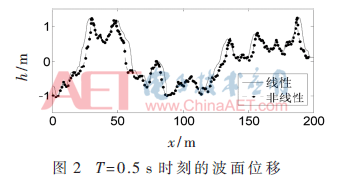
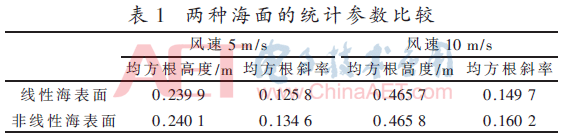
    表1是取不同风速时线性海浪和非线性海浪高度的均方根及斜率的均方根的对比。分析下表可知，随着风速增加，海面的波面位移变大，斜率也增大，说明海面的粗糙度变大。并且两者的均方根高度差别不大，但是非线性海浪的均方根斜率明显比线性海面略大。

    海面大尺度的斜率分布反映了海面的粗糙程度，而海面的电磁散射会受其影响。图3中的(a)和(b)分别给出了取T=0.5 s时刻图2中两种海面斜率的概率密度函数（Probability Density Function，PDF）和累积分布函数（Cumulative Distribution Function，CDF）。通过比较可知，线性海浪的斜率分布是高斯的，而非线性海浪的斜率分布与高斯分布有偏差。并且线性海面的斜率集中在较小值，分布较为平均，而尖波模型得到的非线性海面更容易出现特别大和特别小的斜率。

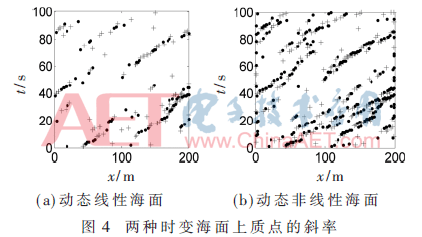
    为了便于观察时变线性和非线性海面上离散点的斜率随时间的变化趋势，可以把斜率超过0.3的质点用点标示（·）出来，斜率低于-0.3的质点用加号（+）标示。如图4所示，时间取100 s，其他仿真参数同上。横轴表示海面的水平距离，纵轴表示海面斜率随时间的变化。由图可知，非线性海面的斜率取值变化更大。相较于线性海面，动态非线性海面上具有较大斜率的质点数量有所增加，而且斜率较小的质点数量也明显更多。

3.2 多普勒谱对比分析

    入射电磁波频率取f=2.85 GHz，海面上方10 m处风速取5 m/s。海面长度L取200 m，入射角设为60°，入射锥形波的波束宽度因子g取L/6，后向散射取θ_s=-θ_i，用水平极化方式。时变海面的时间间隔取0.007 8(1/128) s，时间离散点数设为512，计算这4 s内时变海面的电磁散射，多普勒谱的频率分辨率为0.125 Hz。图5表示基于时变线性海面模型与尖波模型计算得到的多普勒谱。从下图可以看出，非线性海面的回波多普勒谱的谱宽稍大一些，可能因为考虑了海面的非线性效应后，海面波浪的运动速度变快。

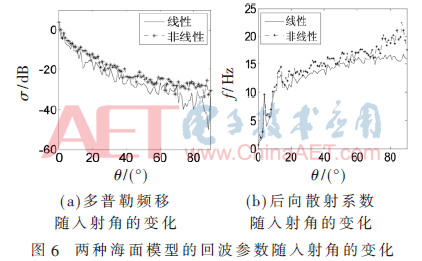
    入射角取0~90°，其他仿真条件同上，海面散射计算的样本数为100。从图6(a)可知，当电磁波近似垂直入射时，海面的镜面散射机制起主导作用，产生的回波功率较大，因此后向散射系数也较大，并且两者的后向散射系数没有区别。当入射角变大时，布拉格共振散射变强，镜面散射减弱，回波功率变小，因此后向散射系数变小，并且非线性海面的后向散射系数略大。观察图6(b)可知，对于两种不同的海面模型，入射角较小时，海面主要是镜面散射，多普勒频移很小；随着入射角变大，海面的布拉格共振散射变强，频移快速增加；而当入射角增大至掠入射时，频移增加的趋势变慢，并且非线性海面的频移较大。

4 基于仿真数据的海浪反演算法验证

4.1 多普勒谱建模

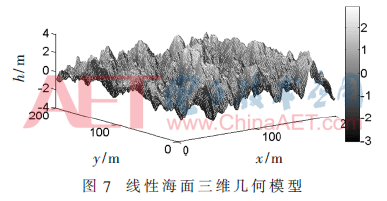
    取t=0.5 s时刻，十米风速取10 m/s，风向角设为0°，海面长度取200 m，距离取200 m。x轴为海面水平长度，y轴为海面距离，z轴为海表面高度起伏。图7给出了基于双叠加法生成的线性海面三维几何模型。

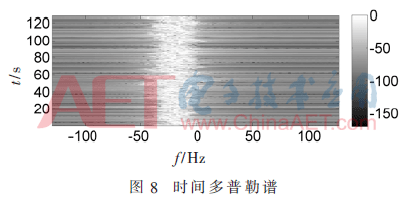
    入射波频率设为2.85 GHz，入射角取0°，用水平极化方式，其他条件同上。以0.003 9 s的时间间隔让图7生成一系列动态海面，每0.5 s（即128个时间点）构成一个多普勒谱，时间长度取128 s，由连续的动态海面生成256个多普勒谱样本。图8为128 s内得到的256个时间多普勒谱。横轴为频率，纵轴为时间。再根据本文的算法生成非线性海面的回波多普勒谱。

4.2 基于建模数据的海浪反演算法验证

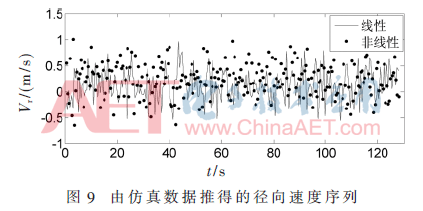
    根据经典的功率谱估计方法求得多普勒谱的中心频率，再由多普勒谱频移计算得到径向速度序列和速度谱。从建模得到的线性和非线性多普勒谱中求得的速度序列如图9所示，该速度序列的时间分辨率为0.5 s，共256个数据点，总时长为128 s，由图可知，速度序列呈现出很好的海浪起伏特征。

    采用海浪反演算法由径向速度谱推导得到海浪谱，并对其进行海浪参数提取。图10为根据海浪反演算法提取的海浪谱，由图可知，非线性海面建模计算出的回波多普勒谱反演误差较小，与实测数值更接近。

5 结语

    本文在时变线性海面和CWM非线性海面建模的基础上，对比了线性海面模型和非线性海面模型的统计特性，所建立的海面模型基本反映了海况的变化特征。采用一阶小斜率近似方法分析了微波电磁波与海表面的电磁散射问题，然后通过仿真得到了微波雷达的回波多普勒谱，表现了海面的非线性效应对回波多普勒频谱的影响。通过对仿真数据进行海浪反演算法的验证，证实了该仿真模型的有效性。结果表明，进行了非线性修正的海面模型包含了更多海面几何结构的信息，且其电磁散射特性与实际海况的结果更加吻合。仿真得到的多普勒谱信噪比高，不受海浪破碎以及存在目标等因素影响。该算法真实反映了海面非线性特征对微波段回波多普勒谱的影响，其结论有助于分析实测数据中非线性效应对海浪参数反演结果的影响，具有重要的指导意义。

参考文献

[1] CREAMER D B，HENYEY F，SCHULT R，et al.Improved linear representation of ocean surface waves[J].Journal of Fluid Mechanics，1989，20(5)：135-161.

[2] NOUGUIER F，GU?魪RIN C，CHAPRON B.“Choppy wave” model for nonlinear gravity waves[J].Journal of Geophysical Research Oceans，2009，114(C9)：C09012-C09027.

[3] VORONOVICH A.Small-Slope approximation for electro-magnetic wave scattering at a rough interface of two dielectric half-spaces[J].Waves in Random Media，1994，4(3)：337-367.

[4] 侯海平，张本涛，陈标.基于二阶谱的海面微波散射特性仿真[J].青岛大学学报：自然科学版，2006(2)：24-27.

[5] VORONOVICH A.Wave scattering from rough surfaces[J].Springer Berlin，2012，89(2)：529-541.

[6] 刘伟.二维粗糙地海面极化电磁散射的相关问题研究[D].西安：西安电子科技大学，2013.

[7] VORONOVICH A.Small-slope approximation for electro magnetic wave scattering at a rough interface of two dielectric half-spaces[J].Waves in Random Media，1994，4(3)：337-367.