朴红艳1，刘  斌2，王承民3，李宏仲2，刘  涌4，衣  涛3

　　(1.国网上海市电力公司电力科学研究院，上海200437；2.上海电力学院 电气工程学院，上海200090；3.上海交通大学，上海200240；4.上海博英信息科技有限公司，上海 200240）

　　摘  要： 以储能电站、分布式电源和充电站等智能设备接入系统的配电网为研究对象，从全社会的角度出发，分别建立了典型智能设备的成本效益模型。分析了几种设备同时接入系统后配网的综合经济效益，并结合算例对比了智能设备安装在配网的负荷侧和电源侧系统的经济性。结果表明，智能设备安装在负荷侧时经济性较佳。

　　关键词： 智能设备；储能电站；分布式电源；充电站；经济效益分析

0 引言

　　随着经济的快速发展和智能电网技术的进步，各种智能设备在现代电网中发挥着越来越重要的作用。分布式电源、电动汽车和储能系统作为我国智能电网战略的重要组成部分，逐渐被应用于削峰填谷、备用、改善电能质量、提高新能源供电稳定性以及解决资源短缺和环境污染等方面[4-6]。

　　储能电站、分布式电源和充电站等智能设备接入系统会产生良好的经济效益和社会效益。然而各种智能设备的投入使用也需要大量的资金支持，智能设备的接入是否具有经济性，这取决于其经济效益是否可观。对多种智能设备接入系统后配电网进行成本效益分析，不仅可以为投资决策提供科学依据，而且对各种智能设备本身技术和电网建设的发展具有重要意义。

　　文献[7-8]分析了蓄电池储能装置在低储高发套利、延缓电网扩建和降低输电阻塞三方面的价值。文献[9]对蓄电池储能装置在削峰、功率平衡和调节负荷三方面的价值及投资成本进行了建模分析。文献[10]较为全面地考虑了钠硫电池储能装置在延缓电网建设、提供备用、低储高发套利等方面的效益，并建立了其成本效益模型。文献[11]则依据典型日负荷曲线分析了配电网中蓄电池储能系统（BESS）在减少电网扩建容量和降低总网损等5个方面的效益，并与其投资成本和运行维护成本共同建立了综合价值评估模型，使用结合罚函数的粒子群优化算法进行求解，通过算例验证了蓄电池的经济性。文献[12]基于分时电价，建立了充电变功率工况下的充电站经济运行模型，通过遗传智能优化算法合理安排电池组的开始充电时间，从而实现充电站的经济运行。文献[13]从电动车的使用成本、电网资源利用率、土地利用率、节能减排及国家能源安全等角度分析了建设充电站潜在的社会、经济和环境保护等方面的综合效益。文献[14]对基于总费用和考虑变压器过载运行的两种充电站变压器选择方法进行了对比，从而确定合理地变压器配置容量。文献[15]从经济性、可靠性和安全性三个方面建立了综合指标评价体系，利用层次分析法(AHP)对分布式电源并网后对电网产生的影响进行了综合评价。文献[16]研究了分布式电源作为削峰资源时所产生的各类经济效益，并建立了电价效益、线损效益及减排效益3种评估模型。文献[17]建立了不同运营模式下光伏发电并网的全寿命周期成本效益模型。文献[18]分析了分布式电源在降低网损、延缓输配电建设、提高供电可靠性、环境效益、减少购电支出、改善气候等方面的效益，并建立了其效益量化评估模型。

　　以上对蓄电池储能装置、充电站和分布式电源进行价值评估的文献中，只是单纯地针对某一种智能设备接入电网后对其经济效益的影响，缺乏各种智能设备完善的经济评价模型，没有体现出智能装置的安装位置对系统综合效益的影响。本文在综合考虑各种智能设备的全寿命周期成本和效益的基础上，通过算例对多种智能设备分别同时接入系统的负荷侧和电源侧的配电网经济效益进行了估算及对比。

1 多种智能设备经济效益模型研究

　　1.1 储能电站的技术经济模型

　　随着智能电网的发展，大量的分布式电源接入智能配用电系统，城市地区电能需求与新增传输通道的矛盾越来越大，储能技术的重要性日益提高。储能技术已被视为电网运行过程中的重要组成部分。电力系统在引入储能环节后，可以有效地实现需求侧管理，消除昼夜峰谷差，平衡负荷，不仅可以有效地利用电力设备，降低供电成本，还可以促进可再生能源的利用，也可以作为提高系统运行稳定性、调整频率、补偿负荷波动的一种手段。储能技术的应用必将在智能配用电系统中发挥重要作用，并将带来重大变革。目前具有代表性的、技术比较成熟的储能蓄电池技术主要有：铅酸蓄电池、镍镉电池、镍氢电池、锂电池、钠硫电池、液流电池（包括钒电池、锌溴电池）。

　　1.1.1 成本模型

　　(1)投资成本

　　储能电站的投资成本主要包括：规划设计成本、物资采购成本以及工程建设成本。

　　C1=CA Wmax+Cp Pmax(1)

　　其中，CA为单位储能的费用(万元/MW·h)；Cp为电力传输系统以及能量转换控制系统单位功率建造费用(万元/MW)； Pmax、 Wmax分别为储能电站的最大功率(MW)和其储存的最大电能(MW·h)。

　　(2)运行维护成本

　　储能电站的运行维护成本包括运行成本和检修维护成本。

　　C2=(Cy+Cw) Pmax(2)

　　其中Cy、Cw分别为能量存储系统的单位运行费用和单位维护费用(万元/MW)。

　　1.1.2 效益模型

　　(1)减少电网扩建容量

　　通过在配电网中安装BESS，可以使储能站在用电低谷时对蓄电池进行充电，提高电网的负载率，而在用电高峰时，将储存的电能释放到电网中，实现部分负荷就地供电，减少配电网中传输的功率，从而使配电网所需扩建容量减少。所以它在减少电网扩建容量方面的收益等值到每年的现值E1可以表示为：

　　其中，Cd为配电网的单位造价(万元/MW)；?姿d为配电设备的固定资产折旧率；?浊为储能装置的储能效率，包括并网设备的损耗和蓄电池的充放电损耗；Pmax为储能系统长期最大充放电功率，即额定功率。

　　(2)减少电网网损费用

　　储能系统在负荷低谷充电、负荷高峰放电，从而实现削峰填谷，拉平负荷曲线，提高负荷率。研究表明：储能系统在拉平负荷曲线的过程中，能有效地减少系统的总网损。则储能装置的安装所减少的电网网损费用为：

　　荷峰期电网网损节约费用：

　　在储能电站的整个寿命周期中，系统在减少电网网损费用方面的收益为：

　　E2=Wh0+Wl1(6)

　　其中，h0、hi分别为安装储能电站前后荷峰期间的网损率，l0、li分别为安装储能电站前后荷谷期间的网损率；th、tl分别为荷峰、荷谷时间（h）；eh、el分别为峰、谷电价(万元/ MW·h)；N为储能电站的寿命。

　　(3)低储高发套利

　　在峰谷电价下，储能装置在负荷低谷、电价较低时充电，而在负荷高峰、电价较高时放电，在这个低价储电、高价卖出的过程中，实现其显性经济收益的年值E3可表示为：

　　(4)新能源并网备用容量

　　由于新能源发电的随机性会给电网带来冲击，需要电网中配备更多的备用容量来应对新能源发电的波动，储能电站可以快速调节其消耗/发出的功率，可以更好地替代常规电源作为新能源发电的备用容量。为方便计算，将储能装置理想化为均匀充放电，则在充放电期间，其剩余电量在0～Pmax T之间的概率分布为均匀分布，其储存电量期望值为0.5Pmax T，即储能装置可用于调节系统功率的电量期望值为0.5Pmax T。所以有：

　　E4=0.5Pmax Tes(8)

　　其中，es为备用容量的价格(万元/MW·a)；T为储能装置以功率Pmax充电的持续时间（h）。

　　(5)减少缺电成本

　　储能装置带来的可靠性效益难以直接定性评估，但储能电站安装于配电站中，可以在停电时作为应急电源为部分重要用户继续供电，减少该配电站的用户停电损失。为便于衡量和计算，可将缺电成本用由于电力供给不足或中断引起用户缺电、停电而造成的经济损失来表示。

　　E5=0.5Pmax T(1-As)RIEA(9)

　　其中，As为配电站供电可靠度，RIEA为用户停电损失评价率(万元/MW·h)。

　　综合以上分析，储能电站的价值评估模型如下：

　　Es=E1+E2+E3+E4+E5-C1-C2(10)

　　1.2 分布式电源的技术经济模型

　　分布式电源大量接入配用电系统是智能配用电系统区别于传统配用电系统的主要特征之一。发展分布式电源是推进能源生产和利用方式变革，合理控制能源消费总量的重要举措。分布式电源规模较小、布局分散、就近利用、清洁高效，是对传统能源生产和利用方式的重大变革。分布式电源包含多种类型，我国近中期分布式电源的发展重点是分布式光伏、分布式天然气及风能。

　　1.2.1 成本模型

　　(1)固定成本

　　C1=CDi Pmax(11)

　　其中，CDi为分布式电源的购买和安装费用(万元/MW)，Pmax为分布式电源的最大功率(MW)。

　　(2)运行维护成本

　　C2=Cm CDi Pmax(12)

　　其中，Cm为运行维护成本占投资成本的百分比。

　　1.2.2 效益模型

　　DG的效益模型主要体现在环境效益和减少网损效益两个方面。长距离的输电传输不可避免地会产生线损，其损失的程度主要取决于输电线长短以及输电路径的阻塞情况，在用电高峰时期，线损甚至达到 20%。DG在靠近负荷的地方或负荷端接入，在一定程度上能够减少线损。研究表明，系统大小与接入分布式电源的数量和位置相关。当负荷需求较大时， DG的运行能够减少系统线损，而当负荷需求较小时，运行 DG反而会增加线损。

　　减少网损效益El可按照储能电站减少网损效益的公式计算得到，其环境效益即相比于普通电源所减少的环境成本。

　　综合以上分析，分布式电源的价值评估模型如下：

　　Ed=Ee+El-C1-C2(14)

　　1.3 充电站的技术经济模型

　　电动汽车具有显著的节能减排和环保优势，推广应用电动汽车对于保障国家能源安全、实现经济社会可持续发展具有重要意义。随着智能电网的逐步建设以及电动汽车保有量的大幅提高，充换电设施的基础性地位更为突出和重要，其对电网以及电力用户都将产生多方面的影响。因此，分析智能配用电系统中的电动汽车充换电站技术经济特性具有重要意义。

　　1.3.1 成本模型

　　(1)固定成本

　　固定成本主要是充电站的建设成本，它包括配变等基础设备的固定投资成本Cc1、土地使用成本Cc2和充电站整个寿命周期内的人力成本Cc3。

　　其中，Cc0为配变等基础设备的固定单位投资成本(万元/MW)，Pmax为充电站的最大功率（MW），r为贴现率，i为货币膨胀率，N为充电站的寿命年限；S0为单位土地使用成本（万元/h），S1为单位人力成本（万元/年）。

　　(2)运行维护成本

　　Cm=Cm0 Pmax(18)

　　Cm0为充电站的单位运行维护成本（万元/MW）。

　　1.3.2 效益模型

　　(1)充换电收益

　　充换电收益与购电成本对应，是充换电站向电动汽车用户出售电力所获得的收益：

　　E1=365Pmax T(eh-el)N(19)

　　T为充电桩以功率Pmax充电的持续时间（h）。

　　(2)节能减排收益

　　电动汽车的普及将减小传统燃油汽车的需求，从而减少汽车的尾气排放，实现良好的经济效益和环境效益。

　　E2=365TNd Ld(cc Kds+cK+cco Kdco+ccN KdcN+cK)

　　(20)

　　其中，Nd为充换电站在T时间段内的电动汽车数量，Ld为每辆电动汽车每次充电后的平均行驶距离（km），cc、cco、ccN、c分别为煤、CO2、CO、CN化合物和NOx的排放价格(元/kg)；Kds为单量电动汽车的平均节煤系数(kg/km)，Kdco、KdcN、K分别为其对应污染物的减排系数（kg/100km）。

　　综合以上分析，充换电站的价值评估模型如下：

　　Ec=E1+E2-Cc1-Cc2-Cc3-Cm(21)

2 算例分析

　　为了对包括储能电站、充电站、分布式电源多种智能设备接入系统的配电网进行经济效益分析，并对比典型智能设备安装在配网的电源侧和负荷侧两种不同位置时对其经济性的影响，在一配网的负荷侧和电源侧分别安装智能设备并使用上述经济效益模型对其进行经济效益分析。

　　2.1 算例描述

　　该配网是某区域的一条10 kV配电线路，该条线路有62个配变，最长供电半径达到4 km；10 kV线路采用电缆与架空混合接线，其中母线出线端多以电缆为主；10 kV架空线主干线的截面积为铝芯240 mm2、185 mm2、150 mm2；10 kV电缆线路主干线的截面积为400 mm2、240 mm2。供电面积较大，节点较多，有两块重负荷区域，分别为：节点23、25处和节点24处。该配网系统的日负荷曲线如图1所示。

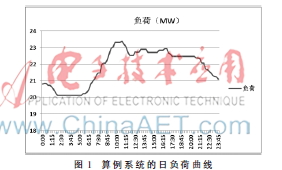
　　由图1可以看出，在一天中，从上午8：45到晚上21:45大概为高峰负荷阶段，凌晨0:00至上午8：00大约为负荷低谷时期。所以根据该配网系统的日负荷曲线，取峰时间13 h，谷时间为8 h。

　　表1～表3分别为经济效益分析中用到的储能电站、分布式电源和充电站的相关参数。

　　2.2 综合效益分析及对比

　　2.2.1 在负荷侧配置智能设备

　　在负荷侧的节点23处安装容量为0.3 MW的蓄电池储能装置，在节点24处安装容量为1 MW的分布式电源并在节点25处配置容量为0.4 MW的充电站。荷峰期智能设备作为电源给负荷提供电能，荷谷期则作为负荷从电网吸收电能，从而实现优化负荷曲线，提高设备利用率以及降低网损等功能。根据上述负荷曲线分析，荷峰时间为13 h，取峰电价为0.088万元/MWh；荷谷时间为8 h，谷电价为0.0408万元/MWh。通过仿真计算得到在负荷侧配置智能设备后该算例系统的综合经济效益为4 501.8万元。

　　2.2.2 在电源侧配置智能设备

　　在靠近电源侧的节点2处安装容量为0.3 MW的储能电站，在节点3处安装容量为1 MW的分布式电源并在节点4处配置容量为0.4 MW的充电站。各种智能装置的成本效益分析同负荷侧，其收益的不同主要在于减少网损费用这一项。通过仿真计算得到在负荷侧配置智能设备后该算例系统的综合经济效益为3 966万元。

　　所以，储能装置安装于配网的不同位置时，会对与网络计算有关的效益组成部分——减少电网网损费用和减少缺电成本方面产生影响。

3 结论

　　本文比较全面地考虑了储能电站、分布式电源和充电站多方面的效益和相应的全寿命周期成本组成，并建立了三者的经济效益模型。以此为基础结合算例的日负荷变化，对多种智能设备同时接入系统的配电网进行了经济效益分析。通过对在负荷侧和电源侧分别安装多种智能设备后的配网进行仿真计算和对比可知，在配网中安装储能设备具有一定的经济性。当智能设备的安装位置变化时，对降低网损带来的收益影响最大，而且这部分收益是体现在智能设备的整个寿命周期中。综上，从经济性的角度出发，将储能设备安装于负荷侧比电源侧的效果更好，这主要是因为将储能装置安装于负荷侧，可以有效降低线路的传输容量，从而有效地降低网损。

参考文献

　　[1] 王志群，朱守真，周双喜，等.分布式发电对配电网电压分布的影响[J].电力系统自动化，2004，28(16)：56-60.

　　[2] 江泽民.对中国能源问题的思考[J].上海交通大学学报，2008，42（3）：345-359.

　　[3] BOULANGER A G，CHU A C，MAXX S，et al.VEHICLE electrification：status and issue[J].Proceedings of the IEEE，2011，99(6)：1116-1138.

　　[4] BHARGAVA B，DISHAW G.Application of an energy source power system stabilizer on the 10MW battery energy storage system at Chino substation[J].IEEE Trans on PowerSystems，1998，13(1)：145-151.

　　[5] BILLINTON R B.Impacts of energy storage on power system reliability performance[C].Canadian Conference on Electrical and Computer Engineering.Saskatchewan，Canada，2005：494-497.

　　[6] JEWELL W T.Electric industry infrastructure for sustainability：climate change and energy storage[C].IEEE Power Engi- neering Society General Meeting.Tampa，USA，2007.

　　[7] Leou Rongceng.An economic analysis model for the energystorage systems in a deregulated market[C].IEEE Interna-tional Conference on Sustainable Energy Technologies，2008. ICSET 2008.Singapore:[s.n.]，2008：744-749.

　　[8] REDRRODT R C，ANDERSON M D，KLUCZNY R M. Economic models for battery energy storage:improvements for existing methods[J].IEEE Trans on Power Systems，1990，5(4)：659-665.

　　[9] OUDALOV A，CHARTOUNI D，OHLER C，et al.Value analysis of battery energy storage applications in power systems[C].2006 IEEE PES Power Systems Conference and Exposition，2006.PSCE’06.Atalanta，GA，USA：[s.n.]，2006：2206-2211.

　　[10] KAZEMPOUR S J，MOGHADDAM M P.Economic viabilityof NaS battery plant in a competitive electricity market[C].2009 International Conference on Clean Electrical Power.Capri，Italy：[s.n.]，2009：453-459.

　　[11] 颜志敏，王承民，郑健，等.配电网中蓄电池储能系统的价值评估模型[J].电力自动化设备，2013，33(2)：57-61.

　　[12] 张帝，姜久春，张维戈，等.基于遗传算法的电动汽车换电站经济运行[J].电网技术，2013，37(8)：2101-2107.

　　[13] 居勇.建设电动汽车充电站的约束条件及综合效益分析[J].华东电力，2011，39(4)：0547-0550.

　　[14] 葛文捷，黄梅，张维戈.电动汽车充电站经济运行分析[J].电工技术学报，2013，28(2)：15-21.

　　[15] 柳睿，杨镜非，程浩忠，等.分布式电源并网的综合评价[J].电力系统及其自动化学报，2013，25(1)：34-39.

　　[16] 曾鸣，田廓，李娜，等.分布式发电经济效益分析及其评估模型[J].电网技术，2010，34(8)：129-133.

　　[17] 苏剑，周莉梅，李蕊.分布式光伏发电并网的成本/效益分析[J].中国电机工程学报，2013，33(34)：50-56.

　　[18] 李德泉，徐建政，杨硕.分布式发电效益分析及其量化模型[J].电力系统保护与控制，2012，40(14)：147-151.