0 引言

    随着现代战争作战环境的不断变化和电子对抗技术的不断发展，战场上多需防止敌机从低空突防，这就要求防空武器系统必须具有良好的低空性能，能够使拦截导弹在沿低空飞行并接近目标的过程中不会因地、海平面的散射杂波干扰而失效^[1]。为此，伪码引信应运而生。此种体制引信具有较好的距离截止特性和较强的抗干扰能力^[2-3]，其安全高度可低至几米，大大提高了导弹的低空性能，是导弹无线电引信的重要发展方向之一。伪码调相引信正是其中的典型代表，它利用伪码类似随机信号的相关特性工作，具有很强的抗干扰能力^[4]。常规干扰方法对付该引信存在着困难且被动的难题。为此，本文提出了一种多时延灵巧假目标干扰方法。

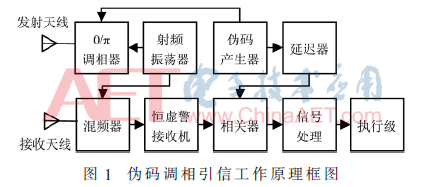
1 伪码调相引信的工作原理

    码调相引信工作原理^[5]如下：伪码产生器产生的两路伪码信号，一路进入调相器对载频振荡器产生的高频载波进行0/π调相，调制后的信号由发射天线向外辐射；另一路伪码信号经过预定延迟作为本地参考码进入相关器。发射信号遇到目标后返回，经接收天线与来自定向耦合器的本振信号进行混频，输出视频信号。视频信号放大后进入恒虚警接收机，由恒虚警接收机进行归一化处理后进入相关器，与本地参考码(即本地延时伪码信号)进行相关处理，输出含伪码自相关函数的相关信号，该信号经幅度检波和信息处理后，输出启动脉冲，触发执行级产生引爆信号。其工作原理框图如图1所示。

    伪码调相引信采用m序列伪码工作，m序列的表达式为：

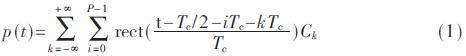
    利用式(1)所描述的伪码波形将高频连续波载波0/π调相后输出，其发射信号可表示为：

式中，A_t为发射信号幅度，p(t)为伪码波形，f_c为射频频载波频率。

    若不考虑干扰，且假设弹目距离为R，则反射回来的回波信号可表示为：

    设伪码延迟器的延迟时间为τ_d，其大小与引信作用距离有关，延迟器输出信号为：

    将式(4)和式(5)所示的两个信号在相关器中进行相关可以得到归一化相关输出为：

式中如果参数选择不合适，cos(2πf_dt)因子对相关器的输出会有较大影响。因此在伪码引信参数设计时，一般选择伪码周期Tr满足：f_dT_r<<1，通常至少有f_dT_r<1/4^[6]，如此，使得多普勒信号幅度在一个伪码周期内基本保持不变。这种情况下，式(6)中的cos(2πf_dt)可以移到积分号外，则：

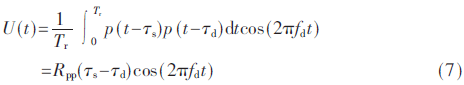
其中，R_pp(τ_s-τ_d)为伪码的自相关函数。当τ_s=τ_d时，R_pp(τ_s-τ_d)取得最大值，此时多普勒信号幅度最大，相关器输出也最大，其中，τ_s=2(L-Vt)/c，L为回波信号达到引信接收灵敏度时的弹目距离，V为弹目相对速度。相关后的信号进入检波器，当检波器的输出信号幅度大于或等于归一化比较电平时，比较器输出启动脉冲，触发执行级产生引爆信号。

2 基于卷积调制的多时延灵巧假目标干扰

    根据对伪码引信的工作原理分析可知，若要干扰信号对伪码引信形成有效的干扰，必须使干扰信号在时域和频域上都与目标回波信号具有较大的重叠或遮盖。同时考虑到干扰信号必须要能通过引信的相关处理环节，因此，干扰信号还需要与引信本地延迟信号同相或基本同相。基于此，本文设计了多时延灵巧干扰信号。

2.1 多时延灵巧假目标干扰信号的数学模型

    设引信发射信号为s(t)，构造干扰信号使得干扰信号为：

    伪码引信通过与本地延迟码的相关处理实现回波中频信号的匹配滤波过程，相关器实际上可以看作频域的匹配滤波器，其冲击响应可以表示为h(t)=s*(t₀-t)，“*”表示取共轭，t₀是使h(t)输出信噪比最大的时延值，也就是本地码的时延。J(t)通过相关器的输出J₀(t)为：

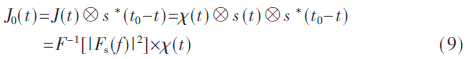
式中，F^-1[|F_s(f)|²]为s(t)的点散布函数，F_s(f)为其频谱。

    对于伪码调相引信而言，不考虑多普勒信号的影响，输入信号的点散布函数为其自相关函数，因此相关器输出可表示为：

    从式(9)、式(10)中可以看出，时域卷积干扰信号经过相关处理后的输出信号由参与卷积的视频干扰信号χ(t)确定，干扰信号可以获得相关处理增益。如果χ(t)为噪声干扰信号，那么卷积调制的干扰信号就能在更小的干扰功率下获得较好干扰效果。

    首先先对χ(t)进行采样得到χ_T(t)，然后把发射信号s(t)通过冲激响应为χ_T(t)的系统得到卷积调制灵巧干扰信号。设采样周期为T，则χ(t)的理想采样信号可以表示为：

    取χ(n)=An表示不同距离的假目标信号的幅度起伏，N为假目标个数，T取为引信发射信号码元宽度。

    综上所述，所构造的干扰信号将时域上造成覆盖真实回波信号多个时域假目标信号，因此，称这种干扰信号为多时延灵巧假目标干扰信号。该信号所产生的假目标在时域上相干的，且信号在频域上与目标信号具有相似的频谱结构；此种干扰在伪码引信相关输出中最多只能造成一个有效相关主瓣峰值，对引信形成欺骗干扰。

2.2 多时延灵巧假目标干扰信号的数字实现算法

    对于经过采样的目标信号，将模拟卷积调制器中的多抽头延迟线用FIFO存储器来代替就可实现如式(17)所示的多时延灵巧假目标干扰信号。这种方法产生的干扰信号相对于输入信号存在一定的固有延时，延时量决定于数字处理器完成N次乘法和1次累加运算的速度。通常可将视频噪声干扰χ(n)和一定长度的信号s(k)的数据事先在干扰设备中存储，然后可以在卷积调制中应用矩阵运算。当χ(n)与s(k)具有相同的长度分别为N和M时，卷积调制输出序列长度为Nh+M-1(h=T/T′)，因此需要先将χ(n)与s(k)以后补零方式延长至长度为Nh+M-1的序列。

    为了提高卷积计算的运算速度，可利用快速卷积算法对延拓后的序列χ′(n)与s′(k)进行FFT变换,并构成乘积序列：

式中，F[]为傅里叶变换算子，然后对序列Y(k)作傅里叶逆变换得到卷积序列y(k)。这种方法虽然看起来计算步骤增多，但由于FFT算法具有极高的效率，从而使得该算法比时域直接卷积计算的速度更快。设计一种采用频域乘积调制算法生成多时延灵巧噪声的算法，其算法示意图如图2所示，具体实现算法如下：

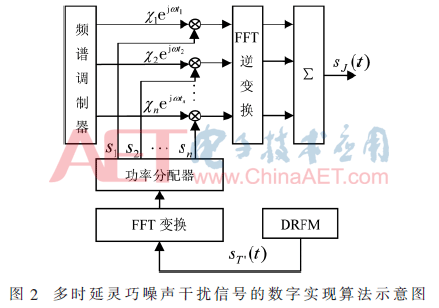
    (1)选取长度为N的噪声序列{χ(n)；0≤n≤N-1}，并将其傅里叶变换后得序列{F[χ(n)]；0≤n≤N-1}；

    (2)对信号采用补零方法使M=2N-1后，得到信号{s(m)；0≤m≤2N-1}，将其傅里叶后分为N个长度为2N-1的序列{F[sl(n)]；0≤l≤N-1，0≤n≤2N-1}；

    (3)应用矩阵算法计算序列F[χ(n)]与F[s_l(n)]的乘积，将得到的N个长度为2N-1的序列{F[y_l(k)]；0≤l≤N-1，0≤k≤2N-2}进行傅里叶逆变换得N个长度为2N-1的序列{y_l(k)；0≤l≤h-1，0≤k≤2N-1}；

    (4)按向量加法运算规则对N个新序列{y_l(k)；0≤l≤N-1，0≤k≤2N-1}进行连加得到输出序列{y(k)；0≤k≤Nh+M-1}。

3 干扰效果仿真及影响因素分析

    多时延灵巧假目标干扰信号是用视频噪声序列卷积调制干扰机存储的引信发射信号生成的，干扰信号的中心频率总是对准引信发射信号的中心频率。干扰机对引信发射信号的数字化采样间隔又是固定的，因此，生成多延时灵巧假目标干扰信号需要考虑两个参数的影响，即噪声采样间隔T和噪声序列的点数N。

    考虑到基于卷积调制的灵巧干扰信号是转发调制后的引信发射信号，与引信发射信号具有较强的相干性，对3种伪码引信具有一致的干扰效果，因此本文只选取伪码调相引信进行分析，其他两种引信与此相似不再分述。下面采用仿真的方法具体分析上述两参数对干扰效果的影响。

    首先考虑卷积噪声序列的点数N，即生成假目标的个数，对干扰效果的影响。仿真参数设置如下：伪码调相引信码元宽度T_c=50 ns，伪码序列长度P=31，载波频率f₀=1 GHz。假设此时对伪码码元宽度Tc的测量是严格精确的，即对视频噪声的采样间隔等于伪码码元宽度，即T=T_c。分别仿真相同干扰功率下N=10、20、30三种情况，仿真结果如图3所示。

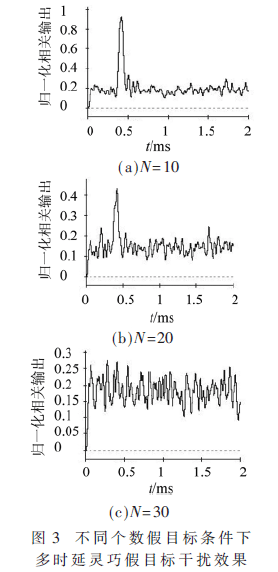
    由图3可以看出，当N=10时，引信自相关输出主旁瓣比约为10.7 dB，可对引信相关检测造成欺骗性干扰；当N=3l时，引信自相关输出主旁瓣比约为0 dB，已难以对伪码引信造成欺骗性干扰。

    再来考虑噪声采样间隔的大小对干扰效果的影响。由上节多时延灵巧假目标干扰信号数字实现方法可知，噪声采样间隔控制的是干扰信号的延时量的大小，也就是所生成的假目标之间的距离间隔。因此，噪声采样间隔的大小将会对一次卷积干扰成功概率产生一定影响。对采样间隔T与伪码码元宽度Tc在误差范围为±20%进行仿真，对干扰成功概率做蒙特卡洛分析，仿真参数设置同上，仿真结果如图4所示。

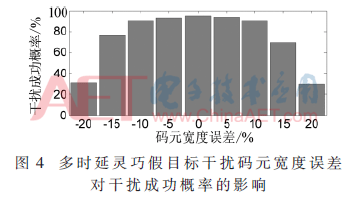
    由图4可知，当采样间隔T与伪码码元宽度T_c误差范围为±10%时，干扰成功概率仍有[90%，95%]的置信区间；当采样间隔T与伪码码元宽度T_c误差达到±20%时，干扰成功概率只有30%左右。

4 结论

    本文通过研究多时延灵巧假目标干扰对伪码调相引信的干扰机理、干扰效果和干扰效能，得出如下结论：

    (1)基于卷积调制的多时延灵巧假目标干扰能对伪码调相引信造成较强的欺骗性干扰；

    (2)影响多时延灵巧假目标干扰对伪码调相引信干扰效果的因素主要有噪声采样间隔T和采样点数N；当采样间隔N与伪码引信码元宽度误差小于±10%时，干扰成功概率可达[90%，95%]的置信区间。

参考文献

[1] 崔屹.国外机载电子对抗设备手册[M].北京：航空工业出版社，1989.

[2] 许凤凯，栗苹.伪码无线电引信干扰机理研究[D].北京：北京理工大学，2011.

[3] 涂友超，曹心缘，鲁犀，等.伪码调相与正弦调频复合调制脉冲串引信压制性噪声调频干扰效果分析[J].信阳师范学院学报：自然科学版，2015，28(2)：163-167.

[4] 何丹娜，张天骐，高丽，等.二次调频-伪码调相复合信号的伪码盲估计[J].电子技术应用，2013，39(5)：100-103.

[5] 隋鉴，李国林，王凌.基于噪声卷积的灵巧噪声伪码调相引信干扰[J].系统工程与电子技术，2014(10)：1924-1928.

[6] 黄光明.伪码体制引信信号特征参数提取及干扰技术研究[D].南京：南京理工大学，2005.

[7] QIU J.Research on essential signification of smart noise jamming[J].Journal of Naval Aeronautical and Astronautical University，2011，26(5)：481-484.