0 引言

    大规模MIMO(Large-scale MIMO)又称Massive MIMO，最早由美国贝尔实验室的MARZETTA T L提出^[1]，该技术在基站配置数十根甚至上百根天线，以获得更大的空间自由度。文献[1-4]研究表明，当天线数目趋于无穷大时，瑞利衰落和加性高斯白噪声等负面影响可以忽略不计，数据传输速率能得到极大提高。大规模天线阵列既带来了性能增益，也带来了前所未有的挑战，如传输方案设计、迅速增加的硬件复杂度和计算量等。大规模MIMO系统中低复杂度、有效的接收算法是该技术从理论到实现的关键。

    近年来，统计学中的一些方法，如基于蒙特卡罗仿真的MCMC检测算法^[5-8]被引入到MIMO系统中，它利用已知符号的后验条件概率来迭代地求出下一个符号的后验条件概率，最后得到发送矢量的后验概率。MCMC方法的性能主要取决于采样点数量和迭代次数，与待估计变量维数无关，可以避免算法复杂度随天线数和调制阶数呈指数级增长的问题。传统的MCMC算法需要经过足够次数的采样后，马尔可夫链才能趋于平衡分布。另外，在高信噪比条件下容易出现“陷入”问题(stalling problem)^[7]，即采样“陷入”某一固定状态，采样状态减少，导致后验概率估计误差。针对上述问题，本文采用超松弛迭代的方法构造马尔可夫链，选择合适的松弛因子加快马氏链的收敛速度。仿真结果表明，该算法提高了系统检测性能，降低了运算复杂度。

1 系统模型

    本文研究的大规模MIMO系统由一个天线数为N的基站和K个单天线用户构成，K≤N，考虑该系统的上行链路，基站端的接收向量表示为：

其中x为K个用户的信号发送向量，x=[x₁，x₂，…，x_K]^T；H为N×K维信道矩阵；n是均值为零、协方差N₀I_N的加性高斯白噪声，n=[n₁，n₂，…，n_N]^T。

    最大似然(Maximum Likelihood，ML)检测是MIMO系统的最优检测算法，通过遍历所有可能的发送信号组合，寻求最优的检测值，即：

式中(χ)^K表示发送向量x的全部可能取值。随着收发天线数及调制阶数的增加，ML算法搜索空间呈指数级增长，实际难以实现。

2 大规模MIMO信号检测算法

    大规模MIMO基站天线数量可能达到几百根以上，传统MIMO的一些准最大似然方法(如基于QR分解的QRM-MLD算法和球形译码(SD)算法)在这里难以采用。探索大规模MIMO系统中高性能、低复杂度的信号检测算法是要解决的主要问题。文献[9]将MCMC方法引入大规模MIMO，并获得了较好的性能。

2.1 MCMC算法

    MCMC检测通过统计抽样获得发送符号矢量，用统计方法估计各符号的后验概率，其性能和运算量与发送信号的维数无关，只取决于采样点数量和迭代次数。

    MIMO系统中，多维信号的联合概率分布如下：

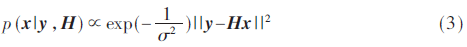
    MCMC算法从条件分布p(x|y，H)中抽取样值x，形成马尔可夫链。MIMO系统中马尔可夫链状态数随x的维数呈指数增加，为了降低采样复杂度，采用Gibbs采样构造马尔可夫链。Gibbs采样^[10]是一种基于条件分布的迭代采样方法，它利用已知符号的后验条件概率迭代地求出下一符号的后验条件概率，最后得到发送信号矢量的后验概率。第t+1次迭代中第k个符号的Gibbs采样过程如下：

2.2 MCMC改进算法

    传统MCMC算法需要经过足够多次迭代才能收敛至平衡分布，提高马尔可夫链收敛速度能够降低检测算法的计算复杂度^[11]，这对大规模MIMO系统尤为重要。因此考虑用超松弛迭代方法(Successive Over-Relaxation，SOR)^[12]来提高马尔可夫链收敛速度。

    将MIMO迭代检测器看作一个随机线性系统，考虑基本线性系统模型如下式：

其中，M=H^HH，b=H^Hy。当K取值很大时，M矩阵求逆运算复杂度很高，考虑采用迭代方法来求解^[13]，由于M是对称矩阵，有：

其中，D是对角矩阵，L是严格下三角矩阵。由Jacobi迭代得到第t+1次迭代的解x^(t+1)：

    超松弛迭代法(Successive Over-Relaxation，SOR)引入了松弛因子ω，以加快迭代矩阵的收敛速度，令：

其中，w=-H^Hn，是均值为零、协方差N₀H^HH的加性高斯白噪声。因此可以由以下分布得到采样值：

    SOR-MCMC检测算法实现过程如下：

    (1)输入接收向量y、信道H、迭代次数T；

    (2)随机产生初始向量x⁽⁰⁾；

    (3)while t<T do

    (4)for k=1：K

    (5){由式(16)、(15)计算由SOR迭代获得的采样点}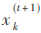

    (6)由获得的采样值，进行对数似然比（LLR）计算，并进行软判决。

2.3 算法复杂度分析

    由上面的分析可知，MCMC算法的复杂度主要集中在由迭代采样构造马氏链，可以先不考虑预条件矩阵处理，即计算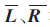和b的运算量。由式(6)可知，传统MCMC算法获得采样值的复杂度为O(N||)，完成一次迭代的复杂度为O(KN||)；而由式(15)，SOR-MCMC中获得采样值的复杂度仅为O(||)，完成一次迭代复杂度为O(K||)。当迭代次数增加时，SOR-MCMC复杂度比MCMC算法低更多，特别适用于大规模MIMO系统。

3 仿真结果及分析

    接下来分析上述算法在不同天线方案、不同调制方式下的检测性能。大规模MIMO系统上行链路收发天线数分别为N和K，记为K×N，令收发天线比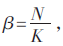要求K≤N。为了便于比较算法性能，采用单用户匹配滤波器检测（MFD）算法近似最佳的MLD算法，即只考虑单个用户发送数据，利用MF方法恢复发送信号。

    首先考虑SOR-MCMC算法中松弛因子ω对误码率(BER)性能的影响。采用4QAM调制，K=16，信噪比SNR=10 dB时，迭代次数T取20，基站天线数分别为8/16/32的仿真结果如图1。可以看到，β较小时，ω对误码率的影响更明显。β较大时，由于天线分集增益，检测性能得到了提高。ω=1.4时，SOR-MCMC算法检测性能最好，后面的仿真中都取该值；ω=1即传统MCMC算法。

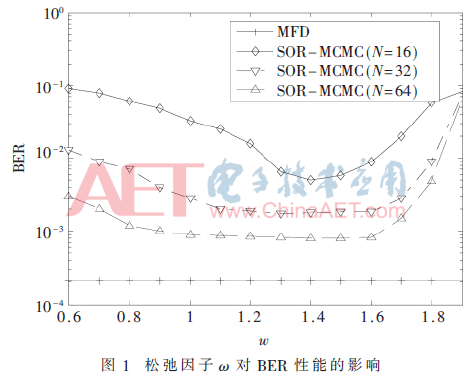
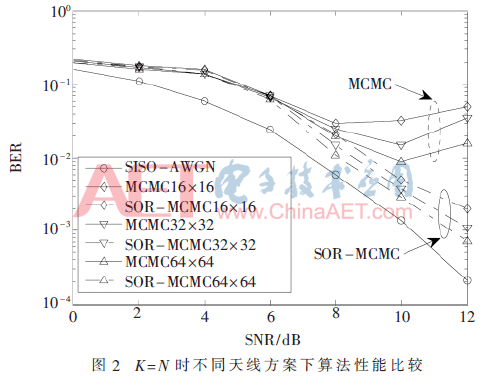
    图2是收发天线数相同时，不同天线配置下几种算法的性能比较，采用4QAM调制，ω=1.4，T=20。由图可知，随着天线数的增加，MCMC和SOR-MCMC算法的性能都有提高，体现了大规模MIMO的特性。高信噪比时，传统MCMC算法由于陷入问题影响了检测性能，而SOR-MCMC算法克服了这个问题。在16×16/32×32/64×64等几种天线配置下，SOR-MCMC的性能都优于传统MCMC方法，且随着信噪比的增加，不断逼近单用户的MFD算法。

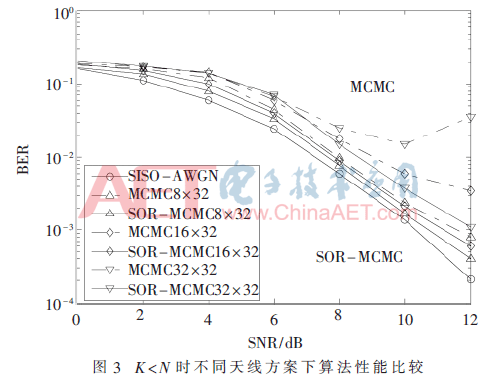
    大规模MIMO的实际应用中，基站天线数一般远大于用户数，下面考虑收发天线数不相等时的算法性能。基站天线数N=32、用户数K分别为8/16/32时各算法性能如图3，仍采用4QAM调制，ω=1.4，T=20。在图3所示的几种天线配置下，SOR-MCMC的性能都优于传统MCMC方法，还解决了传统MCMC方法高信噪比时的陷入问题。β较大时，SOR-MCMC算法性能随着SNR的增大不断逼近MFD。由图3可知，在天线配置为8×32时，SOR-MCMC算法误码率达到10^-3所需的信噪比与MFD相比只相差0.4 dB。

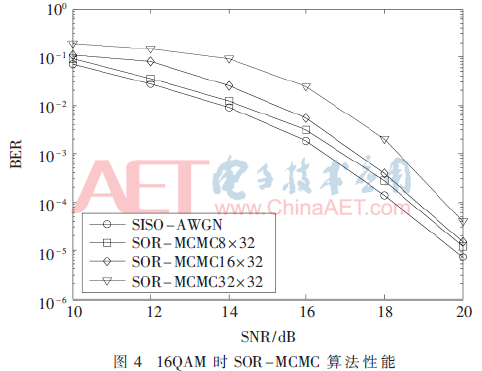
    采用16QAM调制，其余参数不变，SOR-MCMC算法性能仿真结果如图4。可以看到，随着信噪比的增加，SOR-MCMC算法检测性能逼近MFD，即该算法在高阶调制下仍然有效。

4 结论

    本文主要研究大规模MIMO中低复杂度、有效的信号检测技术。MCMC算法因复杂度有限获得较大关注，但传统MCMC算法需要经过多次采样才能趋于平衡分布，且在高信噪比时性能不佳。本文提出了一种改进的MCMC算法，通过超松弛迭代获得Gibbs采样，构造平衡分布为目标分布的马氏链，通过选择合适的松弛因子加快马氏链的收敛速度。仿真结果证明，该算法在不同天线方案、不同调制阶数下，均能获得优于传统MCMC算法的性能，同时计算量更低，非常适用于大规模MIMO系统。

参考文献

[1] MARZETTA T L.Noncooperative cellular wireless with unlimited numbers of base station antennas[J].IEEE Trans.Wireless Commun.，2010，9(11)：3590-3600.

[2] HOYDIS J，BRINK S T，DEBBAH M.Massive MIMO in the UL/DL of cellular networks: How many antennas do we need?[J].IEEE Journal on Selected Areas in Communications，2013，21(2)：160-171.

[3] RUSEK F，PERSSON D，LAU B K，et al.Scaling up MIMO：opportunities and challenges with very large arrays[J].Signal Processing Magazine，2013，30(1)：40-60.

[4] LARSSON E G，TUFVESSON F，EDFORS O，et al.Massive MIMO for next generation wireless systems[J].IEEE Commun.Magazine，2014，52(2)：186-195.

[5] CHEN R，LIU J S，WANG X D.Convergence analyses and comparisons of Markov Chain Monte Carlo algorithms in digital communications[J].IEEE Trans.on Signal Processing，2002，50(2)：255-270.

[6] DOUCET A，WANG X D.Monte carlo methods for signal processing[J].IEEE Signal Processing Magazine，2005，22(6)：152-170.

[7] BEHROUZ F B，ZHU H D，SHI Z N.Markov chain monte carlo algorithms for CDMA and MIMO communication systems[J].IEEE Trans.On Signal Processing，2006，54(5)：1896-1909.

[8] STEPHEN A L，BEHROUZ F B.Implementation of a markov chain monte carlo based Multiuser/MIMO detector [J].IEEE Trans.on Circuits and Systems，2009，56(1)：246-255.

[9] KUMAR A，CHANDRASEKARAN S，CHOCKALINGAM A，et al.Near-optimal large-MIMO detection using randomized MCMC and randomized search algorithms[C].IEEE ICC，2011：1–5.

[10] SPALL J C.Estimation via markov chain monte carlo[J].IEEE Control Systems Magazine，2003，23(2)：34-45.

[11] HASSIBI B，HANSEN M，DIMAKIS A G，et al.Optimized markov chain monte carlo for signal detection in MIMO systems：an analysis of the stationary distribution and mixing time[J].IEEE Trans.Signal Processing，2014，62(17)：4436-4450.

[12] AXELSSON O.Iterative solution methods[M].Cambridge University Press，1994.

[13] GRANT A，SCHLEGEL C.Convergence of linear interference cancellation multiuser receivers[J].IEEE Trans.Commun.，2001，49(10)：1824-1834.