黄雄波

　　（佛山职业技术学院 电子信息系，广东 佛山 528137）

　　摘要：由于自相关函数刻画了时序数据在不同时刻取值的线性相关程度，故其在时序数据的统计分析中得到了广泛的应用。讨论了基于FFT变换的自相关函数计算原理，结合非平稳时序数据的辨识需求，基于自相关函数理论对趋势和周期成份的分离次序以及残留序列的随机类型识别等问题进行了深入分析，进一步提出了一种改进的非平稳时序数据的辨识算法。实验验证了改进算法的合理性和有效性。

　　关键词： 自相关函数； FFT变换；非平稳时序数据；系统辨识

0引言

　　在工程、经济、自然和社会科学等很多领域中，被考查对象在其历史的演变过程中，其相关的物理量常常以一系列随时间而变化的数据序列而被人们记载，这种序列通称为时间序列或时序数据 ［13］。事实上，由于受到诸多偶然因素的影响，时序数据很难用一个精确的数学表达式来描述，但由于它们大都具有统计规律的特性，因此，可以通过对时序数据的辨识和建模，进而达到认识事物、掌握其内在变化规律的目的［46］。

　　一般地说，事物在演变过程中往往具有某种趋势或周期规律的特性，故在现实中所获得的时序数据也就具有非平稳的特点，即序列的均值(一阶矩)为非常数且自相关函数(二阶矩)与起始时间有关［78］。由于非平稳时序数据具有时变的统计结构，故其辨识和建模的过程比平稳时序数据要复杂得多，目前比较有效的做法是［913］：首先从原始序列中分离出趋势和周期成份并分别对它们进行辨识，然后对残留的平稳随机序列建立相应的AR、MA或ARMA模型。本文基于自相关函数的理论，对诸如趋势和周期成份的分离次序以及残留序列的随机类型识别等问题进行了分析，在此基础上，提出一种改进的非平稳时序数据的辨识算法，实验证明改进算法是有效的。

1问题描述

　　1.1时序数据的自相关函数

　　设样本长度为n的非平稳时序数据{y(t),t=0,1,…,n－1}在相邻p时刻的数据取值分别为yt和yt+p，则yt的p阶样本自相关函数的估算值r^(p)可用式(1)进行计算：

　　自相关函数是时序数据的二阶统计特性，它表征了序列数据项之间的依赖程度及趋势的变化情况，据此，可以利用自相关函数的上述性质来识别序列的趋势和周期成份的显著性及它们之间的关联信息等。

　　1.2基于FFT变换的自相关函数计算

　　利用式(1)计算r^(p)时，若序列的样本长度n比较大，则所需要的运算量也随之增加，为了提高运算速度，可以利用快速傅里叶变换(Fast Fourier Transformation，FFT)算法来实现对r^(p)的快速运算［14］。

　　对r^(p)施行Fourier变换，由式(1)有：

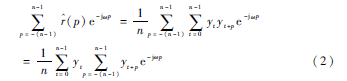
　　为了能用离散傅里叶变换(Discrete Fourier Transform，DFT)来计算式(2)的线性卷积运算，故需要对时序数据y(t)补充n位零数值，得y′(t)，即：

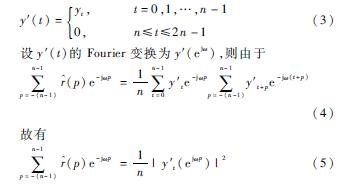
　　综合式(2)~式(5)可知，基于FFT变换的自相关函数的计算流程为：(1)对y(t)补充n位零数值，得y′(t)；(2) 对y′(t)做DFT变换，得到y′(m)；(3) 对1n|y′(m)|2做逆DFT变换，得到r^′(p)；(4)对r^′(p)中0~n的点进行整体右移n位，得到r^(p)。

2非平稳时序数据的辨识改进

　　2.1自相关函数在非平稳时序数据的辨识应用

　　非平稳时序数据y(t)的辨识模型如式(6)所示:

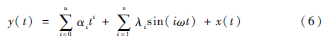
　　其中，∑ui=0αiti是趋势成份，由一个u阶的多项式进行辨识，αi为多项式的各阶次的辨识参数；∑vi=1λisin(iωt)是周期成份，ω为基波角频率，λi为各谐波的幅值；x(t)为残留的平稳随机序列。

　　2.1.1趋势和周期成份的分离

　　对于既有趋势又有周期影响的非平稳时序数据而言，当趋势成份很强时，则其趋势特点表现突出，甚至会把周期特点淹没掉；而当周期成份很强，其趋势特点也有可能显现不出来。 据此，有必要在现有的非平稳时序数据辨识算法的基础上，根据趋势和周期成份在序列中的轻重地位进行依次分离和辨识。

　　对于趋势成份明显的时序数据，由于紧邻的数据项具有相同的取值方向，故其自相关函数的前3~4阶通常会出现正数且具有大于2n的特点；而当序列存在周期长度为L的数据成份时，则由于各个周期内相关位置的数据具有同时为大或同时为小的特点，故其L,2L,…,int(nL)L(int()为取整函数)等各阶次的自相关函数均为正值。依照上述规则，可以通过计算各阶次的自相关函数来判别待辨识的非平稳时序数据是否存在着趋势和周期成份，当仅发现趋势时，则首先分离趋势成份，然后再对残留序列进行周期识别；反之，当仅发现周期时，则首先分离周期成份，然后再对残留序列进行趋势识别；而当趋势和周期同时显著时，则应从原始序列中同时分离这两种数据成份。

　　以趋势和周期成份同时显著为例，其基于最小二乘法的分离过程如下：

　　为满足arg mine=∑nt=0|y(t)－f(t)|2，依最小二乘法有：

　　

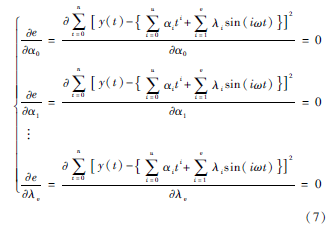
　　求解式(7)的线性方程组［15］，便可得到趋势和周期成份同时显著时的辨识参数向量［α0,α1,…,αu,λ1,λ2,…,λv］T。

　　2.1.2残留序列的平稳性判别及辨识

　　通常，非平稳时序数据y(t)在去掉趋势和周期成份的影响后，其残留序列x(t)可能是一个分段局部平稳、整体平稳或完全随机型的序列，故在残留序列x(t)的辨识之前还应进行随机类型的识别。完全随机型序列其各阶次的自相关函数具有零值的特点；而分段局部平稳或整体平稳的随机型序列在平稳范围内其数据项之间是允许存在自相关的，但数据项xt和xt+p的相关性会随着间隔项p的增大而减少。在工程应用中，若某序列的各阶次的自相关函数满足式(8)，则可把该序列视为平稳时序数据［16］。

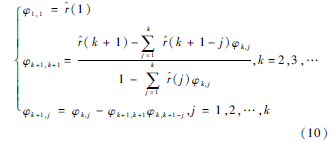
　　式(8)中，符号“&&”为逻辑与运算，“int( )”为取整函数，该逻辑表达式描述了序列的自相关函数的绝对值在1~2阶次时均大于2n，但其后便衰减至－2n,2n区间内。

　　由于完全随机型序列不包含任何形式的模型，故无需对它进行任何的处理；而平稳随机序列则可以采用式(9)的AR模型进行建模：

　　x(t)=φ1xt－1+φ2xt－2+…+φkxt－k+un(9)

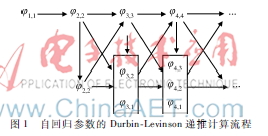
　　式(9)中，［φ1,φ2,…,φk］T为自回归参数向量，un是均值为零、方差为σ2的正态分布白噪声。自回归参数向量［φ1,φ2,…,φk］T可用式(10)的DurbinLevinson递推公式求得，而递推的具体计算流程则如图1所示。

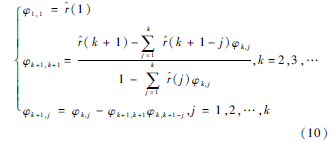
　　对于分段局部平稳的残留序列而言，在辨识之前还应完成各段平稳子序列的划分，即需要确定平稳子序列的段数及各段之间的分割点。根据平稳时序数据的自相关函数特征，可得到如下平稳子序列的分割方法：以1个数据项为步长自左至右地搜索分割点，若新增数据项后的子序列其自相关函数仍满足式(8)中的逻辑表达式，则合并该新增数据项并继续向右搜索；否则以该新增数据项为分割点，新建另一平稳子序列并继续向右搜索；重复上述过程直至遍历整个残留序列为止。完成平稳子序列的划分后，便可根据式(10)中的递推公式求得它们各自的辨识参数向量。

　　2.2非平稳时序数据的辨识改进算法

　　综上所述，可设计如下的非平稳时序数据的辨识改进算法。

　　算法：基于自相关函数的非平稳时序数据的辨识算法。

　　输入：样本长度为n的非平稳时间数据y(t)。

　　输出：趋势成份的辨识参数向量［α0,α1,…,αu］T，周期成份的辨识参数向量［λ1,λ2,…,λv］T，随机成份的辨识参数向量［φ1,φ2,…,φk］T。

　　步骤1设计相关的公用函数模块。

　　模块1依照上述的式(2)～式(5)编写序列的FFT自相关函数计算模块。

　　模块2编写趋势成份显著的识别模块，具体的识别流程为：

　　if((r^(1)>(2/sqrt(n)))&&(r^(2)>(2/sqrt(n)))&&(r^(3)>(2/sqrt(n))))

　　{

　　标识趋势成份显著；

　　}

　　模块3编写周期成份显著的标识模块，具体的识别流程为：

　　for(L=2;L<=int(2/n);L++)

　　{//遍历搜索显著的周期成份

　　if((r^(L)>0)&&(r^(2*L)>0)&&…&&(r^(int(n/L)*L)>0))

　　{

　　标识周期成份显著；

　　}

　　}

　　模块4线性方程组(系数矩阵A=［aij］∈Rn×n)的GaussSeidel迭代求解模块，其迭代求解公式为：

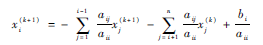
　　步骤2从非平稳时序数据中分离趋势和周期成份。

　　(1)调用公用模块1计算y(t)的r^(1)、r^(2)、…、r^(2n)等各阶次的自相关函数；

　　(2)调用公用模块2和模块3进行趋势和周期成份的识别；

　　(3)对(2)的识别结果进行处理，分“仅趋势成份显著”、“仅周期成份显著”、“趋势和周期成份同时显著”、“趋势和周期均不显著”4种情况；

　　case1://限于篇幅，这里只给出“仅趋势成份显著”的处理流程

　　{

　　(1)基于最小二乘法计算趋势成份显著时y(t)所对应的线性方程组的系数矩阵A；

　　(2)调用公用模块4求得趋势成份的辨识参数向量［α0,α1,…,αu］T；

　　(3)计算残留序列，x(t)=y(t)－∑ui=0αiti－1；

　　(4)调用公用模块1计算残留序列x(t)的r^(1)、r^(2)、…、r^(2n)等各阶次的自相关函数；

　　(5)调用公用模块3对残留序列x(t)进行周期成份的识别；

　　(6)对残留序列x(t)的周期成份识别结果进行处理：

　　if(残留序列x(t)的周期成份显著)

　　{

　　①基于最小二乘法计算周期成份显著时x(t)所对应的线性方程组的系数矩阵A；

　　②调用公用模块4求得周期成份的辨识参数向量［λ1,λ2,…,λv］T；

　　③更新残留序列，x(t)=x(t)－∑vi=1λi(siniωt)；

　　}

　　④转步骤3；

　　}

　　步骤3对残留序列x(t)进行辨识。

　　(1)遍历残留序列x(t)，完成各局部平稳子序列的划分；

　　for(i=0;i<n;i++)

　　{

　　sl=i－d［m］;

　　//计算当前子序列的序列长度，d［m］为第m段平稳子序列的起点位置

　　if(sl>=min)

　　{

　　if((r^(1)==0)&&(r^(2)==0)&&…&&(r^(int(2/sl))==0))

　　{

　　标识当前子序列为完全随机型序列；

　　}

　　else

　　{

　　if((abs(r^(1))>(2/sqrt(sl)))&&(abs(r^(2))>(2/sqrt(sl)))&&…&&(abs(r^(3))<(2/sqrt(sl)))&&…&&(abs(r^(int(2/n)))<(2/sqrt(sl))))

　　{

　　标识当前的第m段子序列为局部平稳子序列；

　　}

　　else//第i项数据为分割点

　　{

　　m++;//局部平稳子序列的段数增1；

　　d［m］=i;//保存第m段局部平稳子序列的分割点；

　　(2)对平稳序列的辨识参数向量进行估计：

　　for(i=0;i<m;i++)//m为(1)确定的局部平稳子序列的段数

　　{

　　while(abs(φi_kk)>(2/sqrt(n)))

　　//取显著性水平α=0.05，若|φi_kk|<2n成立，则认为k阶自相关函数等于0；

　　{

　　利用式(10)对第i段局部平稳子序列的辨识参数向量［φi_1，φi_2，…，φi_k］T进行递推计算；

　　}

　　步骤4输出趋势成份、周期成份及随机成份的辨识参数向量，算法结束。

3实验及结果分析

　　为了验证上述算法的合理性及有效性，这里将分别对趋势成份显著、周期成份显著、残留序列为分段局部平稳的非平稳时序数据进行相关的辨识实验。实验的硬件环境为惠普ProDesk 490 G2 MT商用台式机(CPU:i5-45704×3.2 GHz;内存:4 GB DDR3 1600)，软件环境及开发工具为Windows 8.1+Microsoft Visual C++2010。实验的主要目的是考察改进算法与现有算法之间的辨识精度及计算效能。

　　3.1实验设计

　　不失一般性，实验所用的非平稳时序数据约定满足如下假设：(1)趋势成份为二次多项式α0+α1t+α2t2,且α1α0和α1α2成立，即以直线趋势成份为主；(2)周期成份为一次谐波λ1sinωt；(3)序列的样本长度n=200。

　　分别利用改进算法和现有算法进行如下实验：

　　实验1：趋势成份显著的非平稳时序数据的辨识，所选的数据模型如式(11):

　　y(t)=3t+0.011t2+0.3sin0.785t－0.28y(t－1)(11)

　　实验2：周期成份显著的非平稳时序数据的辨识，所选的数据模型如式（12）：

　　y(t)=0.4t+0.001t2+200sin0.785t－0.28y(t－1)(12)

　　实验3：残留序列为分段局部平稳的非平稳时序数据的辨识，所选的数据模型如式（13）：

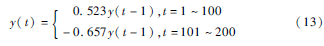
　　3.2实验结果与讨论

　　为了能全面考察改进算法与现有算法的辨识精度，这里引入了均方标准误差(Root Mean Squared Error，RMSE)和平均绝对百分误差(Mean Absolute Percentage Error，MAPE)共两个性能评价标准，具体定义如式(14)和式(15)所示。

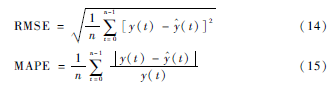
　　式(14)和式(15)中，y(t)为原始序列，y^(t)为辨识序列，n为序列的样本长度。

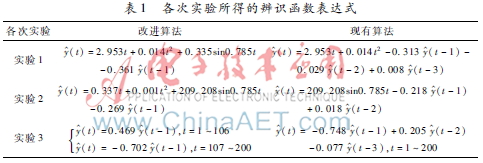
　　实验1~实验3的辨识结果如表1、表2及图2~图4所示。其中，表1为辨识序列的函数表达式，表2为辨识性能的具体数值，而图2~图4则是各次实验的辨识拟合曲线。

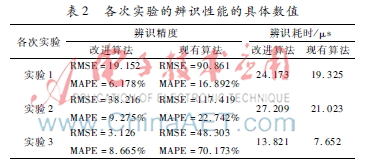
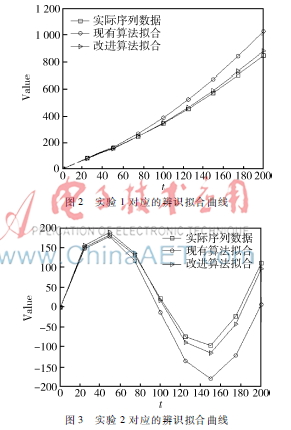
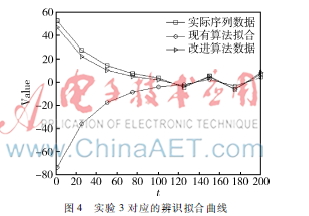
　　从表1的辨识函数表达式易知，对于趋势或周期成份显著的非平稳时序数据而言，由于现有算法没有按照一定的次序进行分离，故不显著的数据成份未能有效地被识别，进而导致了残留随机序列存在一定的偏差。在表2中，根据辨识性能的具体数值可发现，改进算法在增加了一定的计算耗时后其辨识精度有了显著的提高。从图4的辨识拟合曲线则不难发现，现有算法对分段局部平稳序列的辨识效果较差，究其原因是因为用了平稳随机模型来对整体不平稳的序列进行辨识，故不仅存在较大的辨识误差而且辨识序列的模型阶数也出现了增加；而改进算法虽然花费了相当的计算耗时，但能从根本上保证辨识精度。综上所述，本文提出的改进算法对非平稳时序数据具有良好的辨识性能。

4结论

　　本文提出了一种非平稳时序数据的辨识改进算法，由于对趋势和周期成份的分离次序以及残留序列的随机类型识别等细节问题均作了相应的处理，故改进算法的辨识性能有了明显的提升。下一步的主要工作是引入自相关函数的并行快速变换运算，同时研究更为有效的平稳子序列划分方法，以便进一步提升改进算法的计算效能。

参考文献

　　［1］ (德)盖哈德·克西盖斯纳，(德)约根·沃特斯，(德)乌沃·哈斯勒.现代时间序列分析导论［M］.张延群，刘晓飞，译.北京: 中国人民大学出版社,2015．

　　［2］ (美)汉密尔顿.时间序列分析［M］．夏晓华,译.北京:中国人民大学出版社，2015．

　　［3］ 张鹏.飞行数据的时间序列分析方法及其应用［M］.北京:国防工业出版社,2013．

　　［4］ 赵雪岩，李卫华.系统建模与仿真［M］.北京:国防工业出版社,2015．

　　［5］ 萧德云.系统辨识理论及应用［M］.北京:清华大学出版社,2014．

　　［6］ 黄介武.线性与广义线性模型中参数估计的一些研究［D］.重庆: 重庆大学,2014．

　　［7］ 杨继生.非平稳综列数据分析：理论与应用［M］.北京:中国社会科学出版社,2010．

　　［8］ 王宏禹，邱天爽，陈哲.非平稳随机信号分析与处理(第2版)［M］．北京:国防工业出版社,2008．

　　［9］ 黄雄波.时序数据趋势项的分段拟合［J］．计算机系统应用，2015，24(2):174179．

　　［10］ 黄雄波.多周期时序数据的傅氏级数拟合算法［J］．计算机系统应用，2015，24(7):142148．

　　［11］ 黄雄波.时序数据的周期模式发现算法的递推改进［J］．计算机技术与发展，2016，26(2):4751．

　　［12］ MAHESWARAN R, KHOSA R.Wavelet volterra coupled models for forecasting of nonlinear and nonstationary time series［J］．Neurocomputing, 2015,  149(Part B, 3):10741084.

　　［13］ SPIRIDONAKOS M D, FASSOIS S D. Nonstationary random vibration modelling and analysis via functional series timedependent ARMA (FSTARMA) modelsA critical survey［J］．Mechanical Systems and Signal Processing, 2014, 47(12):175224.