文献标识码： A
DOI：10.16157/j.issn.0258-7998.2016.06.030
中文引用格式： 朱晓梅，黄莹，包亚萍，等. 非高斯噪声环境下基于RLS的稀疏信道估计算法[J].电子技术应用，2016，42(6)：109-112.
英文引用格式： Zhu Xiaomei，Huang Ying，Bao Yaping，et al. Recursive least square based sparse channel estimation under non-Gaussian noise background[J].Application of Electronic Technique，2016，42(6)：109-112.
0 引言
为了挖掘无线通信信道的稀疏结构特性，已经提出了各种稀疏LMS信道估计算法[1-3]、稀疏LMF信道估计算法[4-6]以及稀疏LMS/F信道估计算法[7-9]。由于这些算法都是基于LMS、LMF以及LMS/F的误差标准函数，因此相对应的算法会保持相同的收敛速度。实际上，跟这些算法相比，标准RLS算法具有更快的收敛速度[10]。为了尽可能地提高实际无线通信系统中的快速稀疏信道估计能力，发展稀疏RLS信道估计算法是一个潜在的解决方案。通过引入零吸引稀疏约束函数[1]以及近似零范数稀疏约束函数[11]，提出两种自适应稀疏信道估计算法：零吸引RLS（RLS using zero-attracting，RLS-ZA）和零范数RLS（RLS using L0-norm，RLS-L0）信道估计算法。
本文提出两种适合非高斯噪声环境的稀疏RLS信道估计算法。首先，该算法具有比稀疏LMS信道估计算法更简单的计算复杂度。另外，该算法利用了多径信道具有的稀疏特性，提高信道估计性能。最后，通过计算机仿真验证，在不同形状参数的非高斯噪声环境下，该算法都具有较好的信道估计性能以及收敛速度。
1 系统模型和广义高斯噪声模型
1.1 系统模型
假设系统是一个宽带无线通信系统的自适应信号模型，输入为一个长度为N的训练信号序列，在加性非高斯噪声w(n)的干扰下，接收信号y(n)可以表示为：
1.2 广义高斯分布模型
式(1)中的w(n)指的是非高斯加性噪声，在本文中采用的是GGD模型。GGD模型是当前认知无线电网络中三种常用的非高斯噪声模型之一，另外两种分别是高斯混合分布模型和对称α稳定分布模型。
GGD模型的主要思想是保留形如高斯噪声的指数型衰减，通过改变指数参数来获得不同程度的衰减速率，从而模拟实际中不同类型的噪声。GGD在拟合非高斯噪声方面有重要的应用，Chen和G.Gonzalez-Farias等提出GGD可以很好地拟合大气噪声和脉冲噪声[12，13]。
广义高斯分布的概率密度函数为[14]：
实际环境中，非高斯噪声的大样本规模比高斯噪声的高，即非高斯噪声概率密度函数的衰减速率比高斯噪声的低。因此非高斯模型的一个重要特征是比高斯噪声具有更厚重的拖尾。
GGD的密度函数曲线如图1。通过改变α值，可得到不同形状的拖尾，当α>2时，拖尾比高斯的衰减快；当0<α<2时，拖尾比高斯的衰减慢，拖尾较厚重，能够拟合实际非高斯噪声。
2 标准RLS和稀疏RLS信道估计算法
2.1 标准RLS估计算法
先介绍一种标准RLS信道估计算法，代价函数可以写成：
通过式(11)可以看出，标准RLS信道估计算法不能挖掘信道的结构信息。为了有效地挖掘信道结构信息和提高信道估计性能，有必要发展稀疏RLS信道估计算法。
2.2 稀疏RLS估计算法
其中γ表示一个非负的正则化参数，主要用于均衡信道估计误差和稀疏信道的可挖掘稀疏度。通常情况下，针对不同稀疏信道，为了最大限度地挖掘信道的稀疏结构信息，选取γ参数的大小可能会不一样。因此，在实际通信系统中的稀疏信道估计，合理地选取γ也是有效提高自适应稀疏信道估计性能的重要步骤。根据代价函数式(13)，并利用式(8)～(10)，可以推导出稀疏RLS信道估计算法的升级方程为：
3 实验仿真
3.1 仿真环境
该文主要通过改变背景噪声的形状参数(α)，仿真RLS-L0/RLS-ZA和标准RLS，比较其性能。为了达到尽可能平均的信道估计性能，采用1 000次蒙特卡罗仿真次数。仿真环境采用典型的宽带无线通信系统。信号传输带宽为60 MHz，载波中心频率为2.1 GHz。最大信号传输时延为1.06 μs。最大信道时延长度N=128，非零抽头系数个数K=8。为了评估信道的估计性能，均方偏差标准定义为：
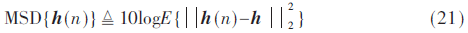
其中E(·)表示数学期望算子。针对实际的信道矢量w，信道抽头系数满足随机高斯分布且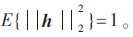
接收信噪比定义为
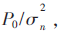其中P0表示接收信号功率，
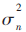表示噪声方差。
3.2 稀疏信道估计性能与形状参数?琢之间的关系
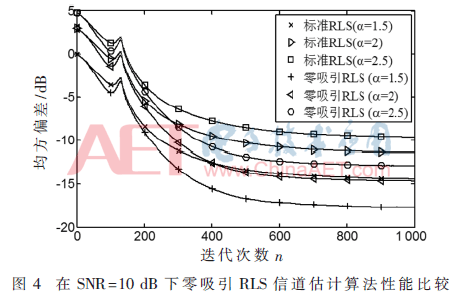
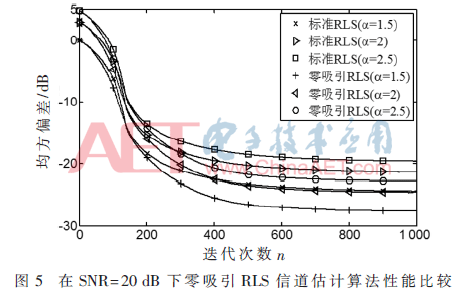
针对3种不同的形状参数，α∈{1.5，2，2.5}，信道稀疏度K=8，遗忘因子λ=0.995，在信噪比分别为10 dB和20 dB的情况下，图2和图3评估RLS-ZA算法的信道估计性能，图4和图5评估RLS-L0算法的信道估计性能。从图2~图5可以看出，针对不同的形状参数，稀疏RLS算法可以达到不同的信道估计性能。本文提出的两种稀疏RLS算法的估计性能都优于标准RLS算法，且形状参数越小，信道估计性能越好。
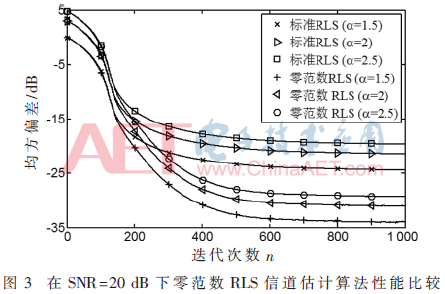
观察图2和图3可得到：形状参数α一致时零范数RLS曲线在标准RLS的下方，说明零范数RLS算法估计性能优于标准RLS；以图2中α=1.5的两条曲线为例，当迭代次数从400增加到800时，两条曲线的差值从1.7 dB上升到3.5 dB左右。随着迭代次数的增加，零范数RLS相较于标准RLS的估计性能优势愈发明显；图3的曲线相较于图2更加平滑且纵坐标数值更小，说明算法在20 dB信噪比的环境下性能更优。
观察图4和图5可得到：α一致时零吸引RLS算法估计性能优于标准RLS；随着迭代次数的增加，零吸引RLS相较于标准RLS的估计性能优势愈发明显；算法在20 dB环境下性能更优。
再分别对比同一信噪比下的图2和图4、图3和图5可以得到，随着迭代次数的增加，同一形状参数α下的零范数RLS算法的信道估计性能比零吸引RLS更好。
4 结论
本文提出一种适合非高斯噪声环境的基于递归最小二乘法的快速稀疏信道估计算法。首先，建立广义高斯噪声(GGD)模型，并在标准RLS算法的基础上引入稀疏约束函数从而提出稀疏RLS算法(RLS-L0和RLS-ZA)。并通过计算机仿真实验验证了这两种算法适合非高斯噪声环境。实验主要研究了提出稀疏RLS算法的信道估计性能与噪声形状参数之间的关系。通过该实验发现，本文提出的算法可以估计出不同形状参数下的广义非高斯噪声信道性能，且形状参数越小，信道估计性能越好。
参考文献
[1] CHEN Y，GU Y，HERO A O.Sparse LMS for system identification[C].Acoustics：Speech and Signal Processing，2009：3125-3128.
[2] GUI G，PENG W，ADACHI F.Improved adaptive sparse channel estimation based on the least mean square algorithm[C].In Wireless Communications and Networking Conference(WCNC)，2013.
[3] TAHERI O，VOROBYOV S.Sparse channel estimation with L P-norm and reweighted L 1-norm penalized least mean squares[C].Acoustics：Speech and Signal Processing(ICASSP)，2011.
[4] GUI G，MEHBODNIYA A，ADACHI F.Adaptive sparse channel estimation using re-weighted zero-attracting normalized least mean fourth[C].In Communications in China(ICCC)，2013.
[5] GUI G，XU L，ADACHI F.Extra gain: Improved sparse channel estimation using reweighted l1-norm penalized LMS/F algorithm[C].China：ICCC，2014.
[6] GUI G，XU L，ADACHI F.RZA-NLMF algorithm-based adaptive sparse sensing for realizing compressive sensing[J].EURASIP Journal on Advances in Signal Processing，2014(1)：1-10.
[7] GUI G，ADACHI F.Sparse least mean fourth filter with zero-attracting l1-norm constraint[C].In Information，Communications and Signal Processing(ICICS)，2013.
[8] GUI G，MEHBODNIYA A，ADACHI F.Sparse LMS/F algorithms with application to adaptive system identification[C].Wireless Communications and Mobile Computing，2013.
[9] GUI G，MEHBODNIYA A，ADACHI F.Least mean square/fourth algorithm for adaptive sparse channel estimation[C].In Personal Indoor and Mobile Radio Communications(PIMRC)，2013.
[10] EKSIOGLU E M.Group sparse RLS algorithms[J]. International Journal of Adaptive Control and Signal Processing，2014，28(12)：1398-1412.
[11] GU Y，JIN J，MEI S.l_0 Norm constraint LMS algorithm for sparse system identification[J].IEEE Signal Processing Letters，2009，16(9)：774-777.
[12] CHEN Y，BEAULIEU N C.Novel low-complexity estimators for the shape parameter of the generalized Gaussian distribution[J].Vehicular Technology，2009，58(4)：2067-2071.
[13] GONZALEZ-FARIAS G，MOLINA J，RODRIGUEZ-DAGNINO R M.Efficiency of the approximated shape parameter estimator in the generalized gaussian distribution[J].Vehicular Technology，2009，58(8)：4214-4223.
[14] ZAHABI S J，TADAION A.Local spectrum sensing in non-Gaussian noise[C].In Telecommunications(ICT)，2010 IEEE 17th International Conference on，2010.