0 引言

    近些年，电力线通信已经成为一个热门的研究话题。然而，高质量的信号在这样一个有强噪声干扰、衰减和多径效应的系统中传输是一个挑战。所以在接收端对信号进行去噪处理是十分必要的。在信号接收端，对接收信号进行分析时，总要提取一些特征值来表征这些信号。所以对信号特征值的提取是识别信号类型的关键。

    目前，信号识别可以分为类间识别和类内识别。类间识别指的是识别不同类型的调制信号，例如ASK、PSK、FSK等信号的识别；类内识别指的是识别同一类信号中的不同调制进制的信号，例如2PSK、4PSK、8PSK。在类内识别方面，HO K C等人^[1]使用小波变换方法成功识别出了BPSK和4PSK信号；POLYDOROS A和KIM K^[2]提出了最大似然比调制识别器，它成功地识别了BPSK和QPSK信号。在类间识别方面，KANNAN R和RAVI D S^[3]使用离散小波变换成功识别出DPSK、PSK和MSK；HAZZA A^[4]等人提出基于特征的方法成功识别出FSK、ASK、PSK、QAM等信号，但是所设计的识别器计算量比较大。

    在识别PLC信号方面，本文采用的是统计模式识别方法^[5-6]，这种方法计算量比较小，容易求解。本文针对文献[1]所提出的识别器模型，改进并设计了一种算法简单、计算量较小的信号识别器。在低信噪比的情况下，识别效果也是比较理想的。基于近似实际的电力线通信信道的仿真结果和比较试验显示出本文所改进和设计的识别器的有效性。

1 信号模型

    设r(t)为接收到的信号的复数模型：

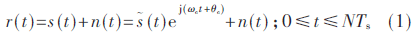
其中s(t)是调制信号的复数形式，n(t)是电力线信道的背景噪声，ω_c是载波频率，θ_c是载波相位。

    对于多进制信号(MQAM、MPSK、MFSK、MASK)的表达式，许多文献已经给出，而本文采用是文献[7]给出的。

2 噪声模型

    实际电力线的噪声包括两部分：背景噪声和脉冲噪声^[8-9]。本文的背景噪声采用概率密度服从Nakagami-m分布的模型来表示^[10-12]。文献[13]验证了PLC系统中的该噪声模型的可行性。本文只研究背景噪声，并且忽略频率衰减性对PLC系统的影响。背景噪声的特征向量(X)服从Nakagami-m分布，其概率密度函数为：

其中，Γ(*)是伽马函数，

Ω是背景噪声的平均功率，定义为这里E[*]表示期望，m是Nakagami-m的参数，即形状因子，表示衰减的严重程度。m=E[X²]/E[(X²-E[X²])2]≥0.5。图1为Ω=2、m=2下的背景噪声仿真图。

3 Haar小波变换的特征

    对于任意函数s(t)∈L²(R)的连续小波变换的定义为：

    Haar小波是紧支集的标准正交小波，并且Haar小波变换也是很容易计算的。所以本文采用Haar小波函数，它的定义表达式可参见文献[14]。

    为了数值计算，式(3)中的积分要用求和代替。令t=kT=k，b=nT=n，于是连续小波变换(CWT)变成：

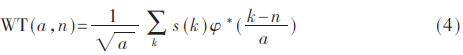
    为了计算方便，假设码元周期是抽样时间的整数倍。表1给出了QAM、ASK、PSK、FSK 4种信号的Haar小波变换，文献[1]给出了PSK、FSK推导过程。

    从表1可以看出，4类信号的小波变换系数幅值是只与尺度a、载频ω_c有关，与n无关的常数。当在单尺度条件下MASK信号小波系数幅度阶梯层数应为该信号的幅度层数M；MFSK信号的小波系数幅度阶梯层数应为该信号的载频层数M；MQAM信号的码元变化引起信号幅度或相位发生变化时，小波变换系数幅度也跟着发生变化，所以MQAM的Haar小波变换系数幅度值为多阶梯并且有许多峰值的函数；MPSK信号的小波系数幅度值随相位的变化而变化，当有相位变化时就会出现峰值，所以MPSK的小波变换系数幅值只有一层。通过信号的小波变换系数幅值的层数可以判断调制信号的进制。所以本文设置两个层数门限N1和N2，它们分别为3和6，当层数大于等于N2时判为八进制调制，大于N1且小于N2时判为四进制调制，小于等于N1时就判为二进制调制。

4 识别器的设计

4.1 特征提取

    通过表1各信号小波变换系数幅值表达式可知，对于MFSK、MASK和16QAM信号，当码元的幅度、频率发生变化时，这些信号的小波变换系数的幅度上也会变化，所以很难从小波变换系数幅度特征值来区分这三类信号。通过已知的知识，MASK和16QAM调制信号波形有幅度、相位以及振幅包络的变化；而MPSK调制信号的波形只有相位的变化，振幅包络是恒定的。为了判别信号的振幅包络是否恒定，本文提取数字调制信号的幅度方差σ²，其定义为：

    设定门限TH1、TH2，当σ²>TH1时判为MASK，当TH1>σ²>TH2时判为16QAM，当σ²<TH2时判为MFSK或MPSK。MFSK的小波变换系数幅度为阶梯波，而MPSK小波系数幅度通过中值滤波后为一直流电平，这两类信号小波系数幅度方差有着明显区别，本文设定一门限TH3，当σ²>TH3时判为MFSK，当σ²<TH3时判为MPSK。表2就是通过该方法计算出的幅值方差。

    从表2中可以看出，调制信号的幅度方差σ²能很好地区分出振幅是否变化的信号，并且服从Nakagami分布的背景噪声对信号幅度方差σ²影响不是很大，在低信噪比下信号区分度还是比较理想的。根据TH1、TH2这两个门限能够有效地识别出三类信号：MASK，16QAM和MFSK、MPSK。

    为了识别MFSK和MPSK信号，需要进一步对这两类信号进行处理。在文献[15]中已经对峰度作了详细的介绍。峰度可以使参数保持信号原有的分布特征，在低信噪比的情况下可以减小了孤立采样点所带来的影响。假设信号的特征向量为X_i(i=1，2，…，n)，那么峰度的定义^[15]为：

    由表1可知，虽然MFSK信号的小波变换系数幅值是一个多峰值阶梯函数，但由于峰度本身的特性，MFSK信号的峰度却很小。而MPSK信号的小波变换系数幅值是一个常量，它的峰度却较大。因此，可以在两类信号的峰度值之间找到一个阈值TH3。当峰度值大于TH3时，则判为MPSK信号，反之，则判为MFSK信号。

4.2 分类器的结构

    经以上分析，可以画出图2所示的分类器结构。它由三部分组成：(1)计算调制信号的幅值方差，根据计算出的结果设置门限值，可以区分出MASK，16QAM和MPSK、MFSK三类信号。(2)根据MPSK和MFSK信号小波变换系数幅值的峰度值得到阈值TH3，这样可以将MPSK、MFSK信号区分出来。(3)根据信号的小波变换系数幅值的层数可以实现各调制信号的类内识别。图1中C表示数字信号的小波变换系数幅值的层数，N1、N2是设置的层数门限值，分别为3和6。第（2）部分中TH3的值是根据文献[16]中提出的方法进行确定的，本文中TH3取2.97。

5 仿真结果

    根据以上的分析，给出所设计分类器的识别效果。本文中所识别的信号分别是2ASK、4ASK、2PSK、4PSK、8PSK、2FSK、4FSK、8FSK、16QAM。信源比特流长度为40，载波频率为5 kHz，采样频率为50 kHz，码元周期为1 s，每个符号内的采样点数为50。在仿真中取门限TH1为0.3，门限TH2为0.07，阈值TH3取2.97。层数门限N1设为3，N2设为6，当层数大于等于N2时判为八进制调制，大于N1且小于N2时判为四进制调制，小于等于N1时就判为二进制调制。

    表3和表4所示是在进行200次独立试验后得到的统计结果。从表3和表4可以看出，在类实际电力线通信信道环境下，当信噪比为5 dB时，数字信号类间的识别可以达到100%；MASK的类内平均正确识别率在95%左右，MPSK和MFSK的类内平均正确识别率均在96%左右。

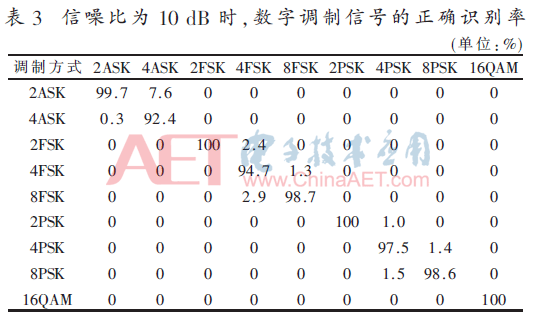
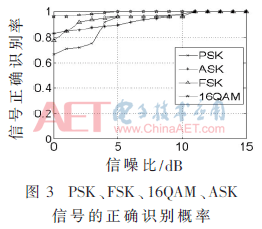    图3所示的PSK、FSK、16QAM、ASK信号的正确识别概率是在1 000次独立的实验基础上统计出来的平均正确识别概率。从图3可以看出，当信噪比为11 dB时，各类信号的正确识别率都可以达到100%；当信噪比为0 dB时，除了MPSK信号外，其他信号的正确识别率都在75%以上，可能是选取的门限值将MPSK信号判为16QAM或者MFSK信号。图4、图5和图6分别是MFSK、MPSK和MASK、16QAM信号的类内识别概率。从这三幅图中可以看出，当信噪比为0 dB时，它们的类内正确识别概率均可达到75%以上；当信噪比为5 dB时，它们类内的识别率可以达到90%以上。从图7中可以看出，当信噪比为5 dB时，信号的正确识别概率将会达到90%以上。

6 结论

    本文采用小波变换识别数字调制信号的方法，设计了用于识别数字调制信号类型的识别器。在电力线背景噪声下，该识别器在MFSK、MPSK、MASK、16QAM几类信号的类间和类内识别效果是比较理想的，且本文所设计的识别器与文献[1]设计的识别器相比，具有计算简单、计算量比较小的特点。首先，识别器根据数字调制信号的幅度方差对信号进行类间判别，然后计算MPSK、MFSK信号的峰度值，作出峰度值的概率密度曲线，找出上述曲线的交叉点确定识别的阈值TH3，最后根据信号的小波变换的系数幅值，确定信号幅值的层数，进而实现信号的类内识别。在类间识别过程中，当信噪比为0 dB时，信号的识别率可以达到80%左右；当信噪比为10 dB时，信号的识别率可以达到99%左右。在MPSK、MFSK识别过程中，当信噪比为5 dB时，信号的识别率可以达到95%左右，但是当信噪比较小时，信号的正确识别率就不是很理想，这可能与阈值的选取有关。在信号类内识别中，只要信噪比在5 dB以上都可以达到良好的效果。所以在电力线通信中，尽量采用MFSK、16QAM或者MASK调制方式对信号进行调制，一方面可以提高抗噪声性能，另一方面可以提高信号的正确识别率，为后期的信息识别提高效率。

参考文献

[1] HO K C，PROKOPIW W，CHAN Y T.Modulation identification of digital signals by the wavelet transform[J].IEE Proceedings-Radar，Sonar and Navigation，2000，147(4)：169-176.

[2] POLYDOROS A，KIM K.On the detection and classificationof quadrature digital modulations in broadband noise[J].IEEE Truns.Commun.，1990，38(8)：1199-1211.

[3] KANNAN R，RAVI S.Digital signals classification in cognitive radio based on discrete wavelet transform[C].2012 Internetional Conference on Control Engineering and Communication Technology，2012：870-873.

[4] HAZZA A，SHOAIB M，ALSHEBEILI S A，et al.An overview of feature-based methods for digtal modulation classification[C].2013 1st International Conference on Communications，Signal Processing，and their Applications，2013：1-6.

[5] NANDI A K，AZZOUZ E E.Algorithms for automatic modualtion recognition of communication signals[J].IEEE Trans.Communications，1998，46(4)：431-436.

[6] SHERMEH A E Z，GHADERI R.An intelligent system for classification of the communication formats using PSO[J].IEEE Informatica，2008，32(5)：213-218.

[7] 陈琦珍.数字调制信号方式的小波识别算法研究[D].南昌：南昌大学，2007.

[8] MATSUO H，UMEHARA D，KAWAI M，et al.An iterative detection for OFDM over impulsive noise channel[C].Proceedings of the 6th International Symposium on Power-Line Communications and its Applications(ISPLC)，2002：27-29.

[9] BALAKIRSKY V B，VINCK A J H.Potential limits on power-line communications over impulsive noise channel[C].7th ISPLC in Proc.，2003：32-36.

[10] MENG H，GUAN Y L，CHEN S.Modeling and analysis of noise effects on broad-band power-line communications[J].IEEE Trans.Power Del.，2005，20(2)：630-637.

[11] KIM Y，OH H M，CHOI S.Closed-form expression of Nakagami-like background noise in power-line channel[J].IEEE Trans.Power Del.，2008，23(3)：1410-1412.

[12] KIM Y，RHEE S W.BER performance of binary transmitted signal for power line communication under Nakagami-like background noise[J].Journal of International Council on Electrical Engineering，2014，4(1)：54-58.

[13] Zheng Tao，Yang Xiaoxian，Zhang Baohui，et al.Statistical analysis and modeling of noise on 10-kv medium-voltage power lines[J].IEEE Trans.Power Del.，2007，22(3)：1433-1439.

[14] 张德丰.Matlab小波分析与工程应用[M].北京：国防工业出版社，2008.

[15] 陈桂明.MATLAB数理统计(第6版)[M].北京：科学出版社，2002.

[16] Meng Lingling，Si Xiujie.An improved algorithm of modulation classification for digital communication signals based on wavelet transform[C].Proceedings of the 2007 International Conference on Wavelet Analysis and Pattern Recognition，2007：1126-1231.