黄骥，许威威，刘复昌

　　（杭州师范大学 杭州国际服务工程学院，浙江 杭州 311121）

　　摘要：为提高检索精确度，提出了一种利用核线性分类分析来对模型特征进行优化的新方法。其主要思想是通过满足Mercer条件的非线性映射将低维空间下线性不可分的样本映射到高维空间，在高维空间中利用线性分类分析将原有的三维模型特征投影到特定的子空间。该方法能够在保持类间距离基础上得到具有鉴别信息的低维特征用于三维模型检索。实验结果表明，核线性分类分析方法速度较快，可在秒级完成三维特征优化，同时优化特征在本文测试数据集上可平均提高搜索准确度15%。

　　关键词：三维模型检索；特征优化；线性分类分析；核线性分类分析；形状分布；形状直径函数

　　0引言

　　三维模型是应用广泛的多媒体数据类型。随着三维建模技术的发展，三维模型的数量快速增长，形成了较大规模的三维模型库。因此，三维模型检索，即如何在三维模型库中高效地检索所需模型，已成为当今多媒体等领域中研究的热点问题之一［13］。

　　三维模型检索算法主要基于特征的匹配，即利用特征相似度来排序库中的模型。研究人员已设计大量三维模型的全局特征，如形状分布、形状直径函数（Shape Diameter Function,SDF)等［45］，在三维模型检索系统应用较早。同时三维模型的局部特征（如热核等）也已应用于解决部分模型检索的问题［6］。虽然由现有的特征能得到较满意的检索结果，但因三维模型的客观性，手工设计的特征的识别能力总有其局限性，查询结果的质量仍有提升空间。

　　本文的主要思想是优化现有的三维模型特征以提高搜索质量，其算法流程如图1所示。特征优化算法以有监督方式进行，利用核线性分类分析（Kernel Fisher Discriminant Analysis,KFD)将三维模型特征映射到高维空间后降维，使降维的特征向量保持类间间距以提高搜索质量。

1核线性分类分析

　　设有观察数据集X，由多个n维向量构成，共分c个类。线性分类分析（Linear Discriminant Analysis, LDA)的目标是计算投影矩阵，使投影后的数据在子空间能有效保持原有空间的距离特征。由于投影空间的维度通常远小于原空间，用投影数据可加速分类，并有效抑制数据噪声 ［78］。图2所示为LDA与P图2LDA（实线）与PCA（虚线）的投影方向及分类边界CA投影方向和分类边界。LDA对类内方差Sw和类间方差Sb的优化可寻找到更恰当的分类边界。

　　为保持距离特征，LDA需在投影的特征空间中最小化Sw的迹并最大化Sb的迹。因此原有高维空间的数据的投影即可有效保持分类的距离特征。Sw和Sb定义如下，其中mk、m分别为第k类和所有样本的平均点。

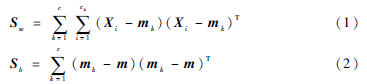
　　为实现数据降维，需要寻找一投影矩阵A使目标函数J(A)最大化，让同类数据点的投影聚在类平均点投影的周围，并让不同类数据点在投影后尽量分开。

　　式(3)的优化可以通过计算投影矩阵A的特征向量得到，且通过A投影的子空间的维度至多为c-1。但当样本在低维空间中线性不可分时，可将样本映射到高维空间实现线性可分。设Φ为低维空间到高维空间F的非线性映射，此时Xi变为Φ(Xi)，mk和m分别变为gΦk和gΦ，Sw和Sb分别变为KΦw和KΦb。为了在F中实现数据降维，式(3)应定义为：

　　然而当F的维数很高甚至是无穷维时，难以直接求解式（4）。为此KFD用点积代替映射（使计算量与高维空间维度无关）解决最大化问题。点积运算可通过Mercer核实现：用核函数K(x,y)计算在F中x与y的点积。由再生核理论，任何第i类的投影向量Wi∈F必位于所有样本在F的张集，故Wi可展开为如下形式：

　　定义(Mi)j、Mj为第j类样本分别与第i类样本、所有样本的点积的平均值，则可得式(6)和式(7) ：

　　其中，E为单位阵，Q中所有元素为1/cj，Kj为第j类核矩阵，其第p行第q列的元素为K(Xp,Xq)。

　　将式(8)和(9)代入式(4)，可得：

　　式(12)的优化方法类似于式(3)。

2三维模型特征选取

　　2.1形状分布

　　由于三维模型形状的客观性，为实现对其相似性进行简单有效的度量，参考文献［5］提出了形状分布算法。该算法采用形状函数来度量，即以模型表面采样点间几何属性（如角度、距离等）的概率分布为比较依据，通过计算概率分布间的函数距离进行相似性判定。

　　常见的形状函数有A3、D1、D2等。考虑实现的难易程度，本文采用D2函数。D2函数采样过程如下：在L次采样中，每次在两个随机选取的面内随机各取一点，计算这两点的距离，由此可得L个距离样本d。

　　为了统计距离的分布情况，统计出在区间［k*p,(k+1)*p)中样本的个数，其中0≤k<L，p=max(d)/L，将各区间样本的个数进行归一化，得到各区间样本的概率。如图3所示，横坐标为采样点的距离，纵坐标为概率密度，右上角为在局部模型上采样的过程。

　　获取到形状分布后，可以用PDF LN或CDF LN算法［5］来计算两个三维模型形状分布的相似度。

　　2.2形状直径函数

　　形状直径函数首先由SHAPIRA L［4］等人提出，并在模型分割与骨架提取算法的应用中取得不错的实验效果。SDF是对三维模型表面上的点与周围体素围成的子模型的直径的度量，用来比较模型的局部相似性。

　　如图4所示，在三维模型表面任意一点处，作一个以该点为圆锥顶点、该顶点法向量的反向为开口方向的圆锥。在圆锥范围内从顶点处引出若干射线与周围三角面相交，去掉与顶点法向量同向的射线，取剩下的射线作加权平均，即得到该点处的SDF值。

3实验分析

　　本文算法中高维特征采用形状分布及SDF［45］。算法测试了普林斯顿大学提供的benchmark库和网上共享三维模型数据库，共500个模型，25个小类。经投影后子空间的维度为20维。本文算法已在PC上实现并实验验证。

　　由于KFD起源于LDA，并较好地完善了LDA无法处理线性不可分样本分类问题的不足，所以为验证本文算法的优劣，本实验对同一个三维模型数据库进行搜索，再将搜索结果分别进行LDA、KFD计算。

　　图5为实验所得到的准确率—查全率曲线。查全率为检索出的相关文件与系统中的所有相关文件之比，准确率为检索出的相关文件与系统中所有检索到的文件之比。准确率—查全率曲线广泛用于评价三维模型的检索质量，反映了准确率与查全率之间的关系。一般前者高则后者低。该曲线越靠上说明准确性越高。如图5，查全率相同时，基于多特征（SD+SDF）的搜索准确率高于基于单特征（SD）；使用KFD优化（SD+SDF+KFD、SD+KFD）的搜索准确率高出未优化特征15%（在SD+SDF+KFD和SD+SDF中，查全率约0.6~0.7时，前者准确率约0.9~0.92，后者约0.6~0.7），而使用LDA优化 (SD+SDF+LDA、SD+LDA)的搜索准确率反而低于未优化的特征。

　　如图6，LDA能解决低维空间中线性可分的分类问题，却不能解决线性不可分的分类问题。此时用LDA优化特征的搜索准确率将低于未优化的特征。如图7，KFD使在低维空间中线性不可分的样本在高维空间中线性可分。在用Fisher准则设计线性分类的总体优化目标函数时，可得到与LDA线性投影类似的结果：在高维空间中线性可分的样本能通过线性投影实现类与类之间的最优分离。因此KFD不仅能使搜索准确率优于未优化的形状特征的搜索准确率，还更优于LDA得到的搜索准确率。

　　参考文献［9］采用深度信念网络进行三维模型检索，其结果评价采用准确率—查全率。当查全率在0.6~0.7时，相应的准确率为0.96~0.98，高于本文算法，其学习时间为120 s，远高于本文KFD的2.5 s。

　　图8~12给出了部分检索结果实例，图中每两行为一个模型的检索结果，第一行为优化前的搜索结果，第二行为使用KFD优化特征后的搜索结果。检索采用基于实例的方法，算法输入一个三维模型的特征向量，用此特征向量与模型库中的模型比较。计算出模型库中的模型与查询实例的相似性，根据相似性从高到低进行排列。以图8为例，本文将图中第1个三维模型作为检索模型，比较了未优化特征和优化特征的效果。从图8第1行得知：第1个模型与第2、3、5、6、8个模型同类，与第4、7个模型不同类，而第4、7个模型却分别排在第5、8个模型之前，显然该检索效果欠佳；从图8第2行得知：未优化特征检索结果得到优化，使得与检索模型同类的模型排名靠前，与检索模型不同类的模型排名靠后，显然该检索效果较好。

4结论

　　本文提出并实现了一种利用KFD对高维三维模型特征进行降维和优化的算法。首先，计算出数据库中三维模型的高维特征向量，由形状分布和形状直径函数组成，然后，将所有三维模型的高维特征向量进行核函数计算，接着利用线性分类分析对计算出的高维特征进行降维优化，利用投影过后的特征进行三维模型匹配。实验结果表明，经过特征优化后，那些与要查找模型相关联较小模型的排序将有效下降。未来工作是进一步寻找更加有效的优化算法，如加快样本在高维空间的非线性映射，进一步提高三维模型检索的质量。

参考文献

　　［1］ 潘翔,叶修梓. 三维模型形状分析和检索［D］.杭州: 浙江大学, 2005.

　　［2］ 杨育彬,林珲,朱庆.基于内容的三维模型检索综述［J］.计算机学报, 2004,27(10): 12971310.

　　［3］ 郑伯川,彭维,张引,等.3D模型检索技术综述［J］.计算机辅助设计与图形学学报,2004,16(7): 873881.

　　［4］ SHAPIRA L, SHAMIR A, COHENOR D. Consistent mesh partitioning and skeletonisation using the shape diameter function［J］.The Visual Computer, 2008, 24(4): 249259.

　　［5］ OSADA R, FUNKHOUSER T, CHAZELLE B, et al. Shape distributions［J］.ACM Transactions on Graphics (TOG), 2002, 21(4): 807832.

　　［6］ BRONSTEIN A M, BRONSTEIN M M, GUIBAS L J, et al. Shape Google: geometric words and expressions for invariant shape retrieval ［J］.ACM Transactions on Graphics, 2011, 30(1): 623636.

　　［7］ BISHOP C M. Pattern recognition and machine learning［M］.New York: Springer, 2006.

　　［8］ Li Jianyuan, Xia Yingjie, Shan Zhenyu, et al. Scalable constrained spectral clustering［J］.IEEE Transactions on Knowledge and Data Engineering, 2015, 27(2): 589593.

　　［9］ Bu Shuhui, Liu Zhenbao,Han Junwei, et al. Learning highlevel feature by deep belief networks for 3D model retrieval and recognition［J］.Multimedia, IEEE Transactions on, 2014, 16(8): 21542167.