0 引言

    矩阵变换器是一种新型的交-交电源变换器，相较于传统的电源变换器，其不需要中间直流储能环节^[1]，能够四象限运行，具有可自由调节的功率因数等诸多优点使其成为了当前电力电子领域的研究热点。但是由于矩阵变换器的电压传输比最高只能达到0.866^[2]，严重影响了其在工程上的应用，因此如何提高矩阵变换器的电压传输比就具有十分重要的现实意义。目前，大多数的文献主要集中在通过对矩阵变换器的控制策略进行研究以达到提升电压比的目的。如文献[3]提出一种谐波注入控制策略，将适当比例的3次谐波注入到输出电压中，但电压传输比也只能提高到1.0左右，而且其输出电压中的谐波含量都会相应增大，效果不甚理想。由此可见，受其现有结构的制约，矩阵变换器的电压传输比很难有较大的提升。而文献[4]提出的“泵式”矩阵变换器则改变了矩阵变换器的拓扑结构，把经典的矩阵变换器电路与CUK斩波电路相结合，可以使电压传输比达到与超过1，但是由于其波形调制和升压过程是独立进行的，所以需要分为两步来实现变压变频，电压传输过程相对复杂。功率开关管在一个周期内动作次数也较多，存在一定的换流安全隐患。因此，本文便从改变矩阵变换器拓扑结构的角度出发，提出了一种新型的“一步式”矩阵变换器。从机理上使三相矩阵式变换器的电压传输比能够突破0.866的瓶颈，使其可以达到和超过1，实现了提升电压比的目的。同时简化了电压传输过程与换流步骤，解决了“泵式”矩阵变换器[4]所存在的缺陷，为工程应用提供了可靠的理论依据。

1 “一步式”矩阵变换器的基本结构

    一步式矩阵变换器的拓扑结构在提升电压传输比的同时，还做到了电压传输比调节电路和波形调制变频电路的合二为一，从而在一个开关周期内，实现了边提高电压边调制波形的功能。将高频升压与斩波调制协调配合，真正达到了升压与变频的一步化。

    一步式矩阵变换器的拓扑结构如图1所示，其中S_jk({j=u，v，w}，{k=a，b，c})为传统矩阵式变换器的9组双向开关，在电路中同时承担升压和变频的任务。而S₂为3组双向开关，在电路中主要起到续流作用。S_jk与S₂均为由两个IGBT反向串联所构成的双向导通功率开关器件^[5]。

    一步式矩阵变换器在一个开关周期内的工作过程可以根据Sjk的通断状态被划分成两个阶段。不同的划分只是为了能更明确地说明其工作原理，并不表示其各部分的工作过程是相互孤立的。设一个开关周期的时间为t，S_jk相应导通的时间为t₁，S_jk断开的时间为t₂，t=t₁+t₂。

    第一阶段：在时间t₁内，9组矩阵开关S_jk根据控制策略相应导通，3组续流开关S₂断开，电源电压经9组矩阵开关后改变频率，经过变频后的电压给电感L₁充电，且同时与电容C₁串联，共同经过电感L₂向负载提供电能。

    第二阶段：在时间t₂内，9组矩阵开关S_jk全部断开，3组续流开关S₂导通续流。电感L₁经过S₂形成回路，给电容C₁充电，其储存的能量转移至电容C₁。同时电感L₂同样经过S₂形成回路，释放能量给负载提供电能。

    由此可见，9组矩阵开关S_jk既起到了改变频率的作用，又提升了电压，所以只要选择适当的t₁和t₂，就可以使负载两端电压在一个周期内始终高于电源电压^[6，7]，从而达到升压的目的。

2 “一步式”矩阵变换器的调制策略

    一步式矩阵变换器采用的调制策略实时计算占空比，控制9组矩阵开关S_jk和续流开关S₂。同时减少了功率开关管在一个周期内的动作次数，保证变频升压电路中的各组双向功率开关在一个周期内均只开通关断一次，简化了其多个双向开关间的频繁换流步骤，同时结合四步换流的换流策略，增强了换流的可靠性，实现了开关间的安全切换。

2.1 9组矩阵开关Sjk的调制策略

    由之前的分析可以知道，9组矩阵开关S_jk在t₁时间内会按照调制策略相应导通，需要注意的是，在t₁内的任意时刻，与同一输出相相连的三组开关管中必须只能有一组开关导通，否则将造成两输入相间的短路^[8]。

    设三相输入电压为U_i，通过9组矩阵开关S_jk后的期望三相输出电压为U_o：

2.2 3组续流开关S2的调制策略

    3组续流开关S2的控制方法相对比较简单，因为由之前的分析可知，它在整个电路中起到的只是维持电流延续的作用，并不需要承担升压或者变频的任务，所以这三组开关在一个周期内任意时刻的通断状态都是相同的，也不需要考虑三相之间的换流问题。在t₁时间内，3组续流开关S₂同时关断，在t₂时间内，3组续流开关S₂同时导通。

2.3 简化功率开关管的动作次数

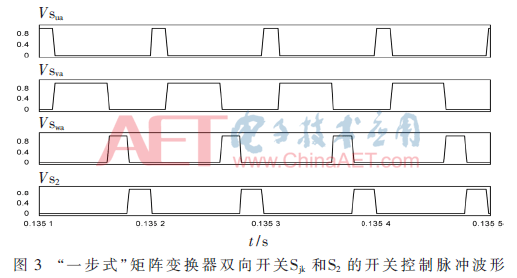
    通过上述的调制策略，就可以确定一步式矩阵变换器中各组开关管在一个开关周期t内的导通状态与导通时间，相比于“泵式”矩阵变换器，新型“一步式”矩阵变换器的9组矩阵开关S_jk在一个周期内均只导通和关断一次，从而简化了其多个双向开关间的频繁换流步骤，增强了换流的可靠性，实现了开关间的安全切换。图2所示为“泵式”矩阵变换器同一输出相各组开关与S₂的控制脉冲波形图。图3所示为“一步式”矩阵变换器同一输出相各组开关与S₂的控制脉冲波形图。一个开关周期均为10^-4 s。

3 “一步式”矩阵变换器的总电压传输比方程

    本文所设计的一步式矩阵变换器的拓扑结构把电压传输比调节电路和波形调制变频电路合二为一，所以它的调压步骤和变频步骤是同步进行的，避免了多余的开关动作和繁琐的升压过程，结构清晰合理，根据其自身特点，推导出的总电压传输比方程具体如下：

    在一个开关周期T内S_jk的工作状态可分为T_on和T_off两个时间段，T_on即对应了之前的t₁，T_off即对应了之前的t₂。

    设S_jk的开关占空比为ds：

    在一个开关周期内，对于电感L₁，在T_on时间内，由电源电压对其进行充电，获取能量。而在T_off时间内，其向电容C₂放电，转移能量。所以根据电磁感应定律得到以下关系式：

    同样在一个开关周期内，对于电感L₂，在T_on时间内，由电源电压与电容C₁共同对其进行充电，获取能量。同时向负载放电，转移能量。而在T_off时间内，其不获取能量，只向负载放电，转移能量。所以根据电磁感应定律得到以下关系式：

    Q即为一步式矩阵变换器的电压传输比。

4 仿真结果

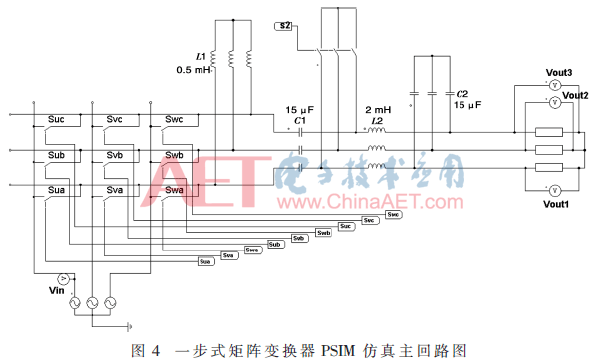
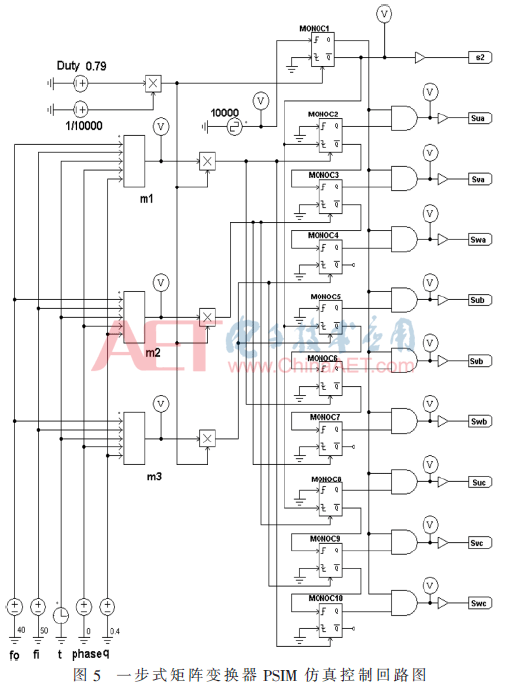
    为验证一步式矩阵变换器拓扑结构与调制策略的可行性，我们采用PSIM 9.0软件作为仿真平台，搭建了一步式矩阵变换器主回路与控制回路的仿真模型，如图4、图5所示。仿真模型中负载的取值为15 Ω，电感L₁为0.5 mH，电感L₂为2 mH，而两组电容C₁、C₂的容量均为15 μF。开关频率设为10 kHz，仿真时长为0.2 s。输入信号为幅值100 V，频率50 Hz的三相正弦交流电，通过改变占空比ds，开关增益q，以及输出电压频率wo这三个变量，观察实际的电压输出波形。

    如图6所示为当输入电压为100 V，50 Hz，开关增益q=0.4，占空比ds=0.79，输出频率为20 Hz，60 Hz，100 Hz时的输出电压波形，从图中可以看出在不同频率下，一步式矩阵变换器的电压传输比均超过1。

如图7所示为当输入电压为100 V，50 Hz，开关增益q=0.4，输出频率为30 Hz，占空比ds=0.75，ds=0.79，ds=0.83时的输出电压波形，从图中可以看出根据ds的改变，输出电压会随之变化。

    如图8所示为当输入电压为100 V，50 Hz，占空比ds=0.79，输出频率为40 Hz，开关增益q=0.3，q=0.4时的输出电压波形，从图中可以看出根据q的改变，输出电压也会随之变化。

    根据上面的仿真模型中所得到的数据，我们绘制了各种情况下一步式矩阵变换器输入输出的电压传输比表格，如表1所示，输入电压幅值均为100 V。

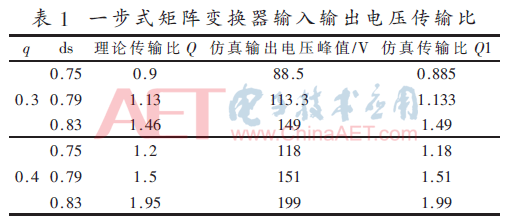
    由上面的仿真结果可以看出，一步式矩阵变换器既保持了传统矩阵变换器变频的特性，同时它的输出与输入电压的传输比突破了0.866的技术瓶颈，达到和超过了1。此外，通过改变ds与q两个变量的数值，把输出电压与输入电压进行幅值对比所得到的仿真结果Q1与理论方程所推导的电压传输比Q近乎相等，同样验证了总电压比传输方程的正确性。

5 结束语

    本文提出了一种新型的“一步式”矩阵变换器拓扑结构以及相关的调制策略，简化了电压的传输过程，增强了换流的可靠性，并通过PSIM仿真软件验证了其可行性与正确性。选择适当的占空比ds与开关增益q，可以使其电压的总传输比突破0.866的瓶颈，达到与超过1。

参考文献

[1] WHEELER P，RODRIGUEZ J，CLARE J，et al.Matrix converters：a topology review.IEEE Trans.IA.2002，129(5)：276-288.

[2] ALESINAETC A.Analysis and design of optimum amplitude nine-switch direct AC-AC converters[J].IEEE Trans.On PE，1989，4(1)：101-112.

[3] 岳周，成运.提高矩阵变换器电压传输比的方法研究[J].计算技术与自动化，2013，32(1)：50-54.

[4] 万衡，陈文博，陈庆安，等.具有高传输比的“泵式”结构矩阵变换器[J].电子技术应用，2010，36(5).

[5] 万衡.单相矩阵式电力变换器的研究与应用[D].上海：华东理工大学，2001.

[6] CHANG J，SUN T，WANG A.High compact AC-AC converter achieving a high voltage transfer ratio[J].IEEE Trans.on Industrial Electronics，2002，49(2)：345-352.

[7] FEDYCZAK Z，SZCZENIAK P.New family of matrix-reac-tance frequency converters based on uni polar PWM AC matrix-reactance choppers[C].13th International Power Electronics and Motion Control Conference.2008：236-243.

[8] 朱贤龙.三相交—交矩阵式变换器及其在电气传动中应用的研究[D].上海：上海大学，2000.

[9] ALESINA A，VENTURINI M G B.Solid-state power conversion：a fourier analysis approach to generalized transformer synthesis[J].IEEE Transactions on circuits and systems，1981，28(4)：319-330.