基于扩展卡尔曼神经网络算法估计电池SOC-AET-电子技术应用

基于扩展卡尔曼神经网络算法估计电池SOC

2016年电子技术应用第7期

韩忠华1，2，刘珊珊1，2，石刚2，董挺3

1.沈阳建筑大学信息与控制工程学院，辽宁沈阳110000； 2.中国科学院沈阳自动化研究所，辽宁沈阳110000；3.中国电子技术标准化研究院，北京100007

摘要： 针对汽车锂电池的荷电状态（SOC）的问题，基于Thevenin电路为等效电路并且应用扩展卡尔曼算法(EKF)结合神经网络算法进行估计。在进行卡尔曼滤波算法估算过程中，需要用到实时的估算模型参数值（最新值），即在不同的SOC下模型的参数不同。传统做法是把SOC与各个参数的关系进行普通的拟合，这种方法在拟合过程中存在较大误差。为了解决这个问题，利用神经网络拟合各个电路模型参数与SOC关系曲线。试验结果表明，与单纯的扩展卡尔曼算法相比，该方法能够准确估计电池剩余电量，误差小于3%。

关键词： 锂离子电池SOC 扩展卡尔曼算法神经网络 RC电路模型

中图分类号： TM92
文献标识码： A
DOI：10.16157/j.issn.0258-7998.2016.07.019
中文引用格式： 韩忠华，刘珊珊，石刚，等. 基于扩展卡尔曼神经网络算法估计电池SOC[J].电子技术应用，2016，42(7)：76-78，82.
英文引用格式： Han Zhonghua，Liu Shanshan，Shi Gang，et al. Estimation of battery SOC based on extended Kalman filter with neural network algorithms[J].Application of Electronic Technique，2016，42(7)：76-78，82.

Estimation of battery SOC based on extended Kalman filter with neural network algorithms

Han Zhonghua1，2，Liu Shanshan1，2，Shi Gang2，Dong Ting3

1.Faculty of Information and Control Engineering，Shenyang Jianzhu University，Shenyang 110000，China； 2.Laboratory of Industrial Control Network and System Shenyang Institute of Automation of China，Shenyang 110000，China； 3.China Electronics Standardization Institute，Beijing 100007，China

Abstract： An extended Kalman filter algorithm(EKF) with neural network is used to estimate the state of lithium battery(SOC)，which is based on Thevenin equivalent circuit. In the process of extended Kalman filter estimation, the real-time model parameters should be updated with the different SOC regard to the different SOC the different model parameters. The traditional approach which has a big error is that the fitting curve between SOC and the various separate parameters is common. To solve this problem neural network is applied to fit curve between the parameters of circuit model and the SOC separately. Finally,the results with the error less than 3% show that compared with the pure extended Kalman algorithm, the method can realize the more accurate estimation of the remaining battery power.

Key words : SOC of Li_ion battery；extended Kalman filter algorithm；neural network；RC equivalent circuit

0 引言

经过近二十年的发展，汽车行业动力蓄电池技术^[1-2]已经成熟。电动汽车由于其零排放、零污染、能源利用率高等优点，在新能源汽车中发展潜力巨大。其中，最重要的一部分就是电池荷电状态的监测^[3]。

电池的荷电状态就是电池在一定放电倍率下，剩余电量与相同条件下额定容量的比值。如果不能准确地估算电池的SOC，就会出现电池过充或过放，造成电池内部损坏。而SOC的准确估算对于电动汽车的正常及健康的运行具有重要意义。目前，国内外对于电池SOC估计^[4-8]的研究较多，例如开路电压法、安时积分法、开路电压法结合安时积分法以及卡尔曼卡波法等。但是，开路电压法在估算电池SOC过程中，需要静置电池很长时间才能估算精确，因此此方法不适合在线估算。安时积分法的缺点是电池的初始值需要很精确，但是随着时间的延长，测量误差会累积导致估算不准确，因此此方法也不适合单独使用。开路电压法结合安时积分法的缺点是，电池容量会随着工况的变化而改变，因此会有累积误差。卡尔曼滤波算法是一种有效的在线估计电池SOC的方法，但是该方法依赖电池模型的精确性，对电池的参数很敏感，电池的性能受很多因素的影响，例如电池工作温度、充放电倍率、自放电倍率以及循环寿命等等。本文暂时不考虑这几种影响因素。综合考虑电池SOC的研究方法，本文采用卡尔曼滤波算法结合神经网络对电池的SOC进行估算，此方法也可以对电池模型内部的参数进行实时估算。

1 等效电路模型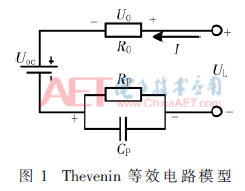

目前，国际上较认可的等效电路模型^[9-11]有：Rint模型、Thevenin模型(RC模型)、PNGV模型、神经网路模型，以及清华大学林成涛等人提出的一种通用非线性模型等。但是在电池SOC评估中，电池的模型不能太简单也不能太复杂，应结合电池的特性进行建模。本文采用Thevenin模型，该模型能够有效反映电池的特性，且简单实用。电池的模型如图1所示。

根据基尔霍夫定律，以图中的电流方向为正方向，可得电路方程：

式中，U_L表示电池的负载电压，U_oc表示电池的开路电压，R₀表示电池的内阻， I表示电池负载电流，U_P表示RC环两端电压，C_P为极化电容，R_P为极化电阻。

2 电池SOC估算

在引言中已经对每个估算方法进行了评价，综合考虑每个估算方法的优缺点并阅读了大量文献发现，现阶段使用较多的卡尔曼滤波算法存在着缺点，因为在进行算法估算过程中，需要用到实时的估算模型参数的最新值，即在不同的SOC下模型的参数不同。当算法估算后得到新的SOC值后就要根据SOC与参数值的关系曲线来确定此时的各个参数值。传统做法就是把SOC与各个参数的关系曲线进行普通的参数拟合，但是这种方法在拟合过程中还存在较大的误差，就会造成利用算法估算电池SOC时出现不太准确的现象。因此，本文针对这个问题进行了改进，利用神经网络算法进行电池SOC与各个参数的拟合，之后利用扩展卡尔曼算法进行估算电池的SOC。

综上所述，本文结合实际情况选择扩展卡尔曼算法结合神经网络方法来计算电池的SOC。神经网络用来拟合各个电池参数(U_oc、R₀、R_P、C_P、τ_P)与SOC的关系曲线，再利用卡尔曼滤波算法估算电池的SOC。

2.1 电路空间方程

根据电池等效电路模型Thevenin电路，结合安时积分法，将系统的状态变量选为电池的剩余电量（SOC）、2个RC环的端电压U_P。以电池的电流i(t)作为激励，电池的端电压U_L作为输出。

状态方程可表示为：

2.2 神经网络拟合

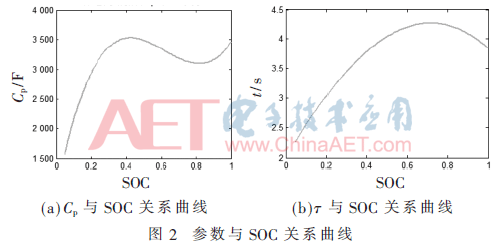
目前，人工神经网络^[12-13]已经发展成为智能控制领域的热点；其结构简单，可操作性强，具有很强的自适应、自学习等优点，因而在函数逼近、模式识别、智能控等领域都有广泛的应用。本文利用神经网络算法拟合出极化电容C_P、时间常数τ等参数与SOC的曲线关系，克服了多项式拟合的大误差现象，使估算更精确，如图2。

2.3 卡尔曼滤波算法

电池模型的状态方程：

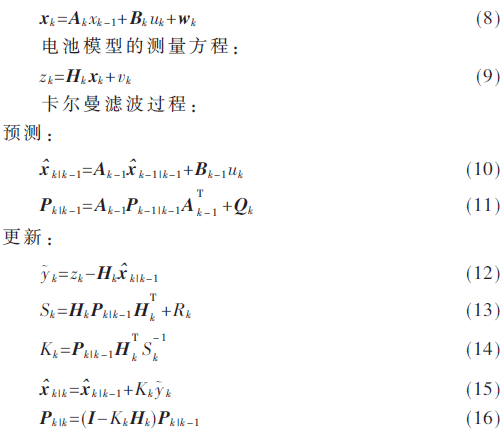
2.4 扩展卡尔曼滤波算法

卡尔曼滤波器主要用来处理线性离散系统，而本文中设计的系统是非线性系统，应该使用扩展卡尔曼滤波算法(EKF)^[14-15]。

对于一个非线性系统，其系统方程为：

3 算法验证

把电池置于室温（25 ℃）环境下，对电池进行恒流放电，放电电流为1/3C。利用扩展卡尔曼算法结合神经网络算法进行估算电池的SOC与现在流行的扩展卡尔曼算法（EKF）的估算结果分别与实际的电池SOC情况做对比，可以看出利用本文中的新算法估算的结果比较准确。图3是两种算法的估算实验结果。

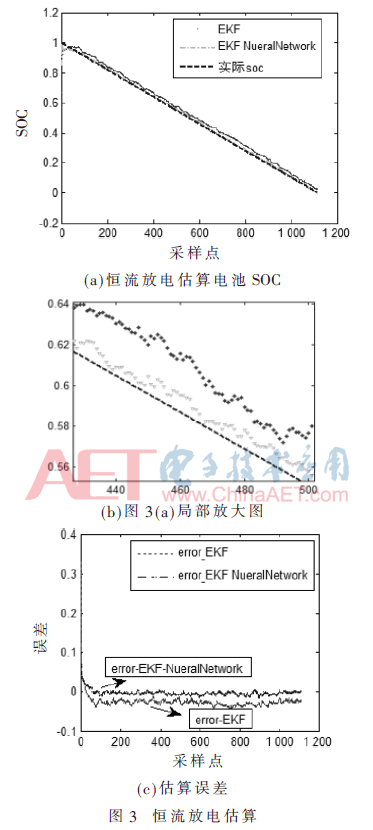
经过恒流放电过程的对比结果可知，利用EKF结合Neural network算法估算电池的SOC效果比单纯的EKF要理想。由误差图3(c)中可以看出，本文估算的误差在3%之内，比单独EKF估算误差5%要小很多。

4 结语

本文提出了扩展卡尔曼结合神经网络算法来估算电池SOC，误差小于3%，与标准的扩展卡尔曼算法的误差5%相比，误差有所降低。该算法能够解决安时积分法对初值敏感的问题，但是此方法没有考虑电池使用寿命因素和自放电因素，而前一因素在实际电动汽车运行有重要的影响，因此，在以后的工作中会进一步考虑电池的循环寿命这一主要因素。实验表明，该算法能够实现在线估算电池SOC，估算精度小于3%。此研究为后续的研究奠定了良好的基础。

参考文献

[1] SCROSATI B，GARCHE J.Lithium batteries：Status，prospects and future[J].Power Sources，2010，195(9)：2419-2430.

[2] 孟良荣.电动车电池现状与发展趋势[J].电池工业，2006，11(3)：202-206.

[3] 谭晓军.电动汽车动力电池管理系统设计[M].广州：中山大学出版社，2011.

[4] 麻友良，陈全世，齐占宁.电动汽车用电池SOC定义与检测方法[J].清华大学学报（自然科学版），2001，41(11)：95-97.

[5] 时玮，姜久春，李索宇，等.磷酸铁锂电池SOC估算方法研究[J].电子测量与仪器学报，2010，24(8)：769-774.

[6] 尹安东，张万兴.基于神经网络的磷酸铁锂电池SOC预测研究[J].电子测量与仪器学报，2011，25(5)：433-437.

[7] 凌国维.基于人工神经网络理论的电动汽车用锂离子动力电池组智能管理系统的研究[D].天津：天津大学，2006.

[8] 何耀.动力锂电池组状态估计策略及管理系统技术研究[D].合肥：中国科学技术大学，2012.

[9] 姜久春，文锋，温家鹏，等.纯电动汽车用锂离子电池的建模和模型参数识别[J].电力科学与技术学报，2010，25(1)：67-74.

[10] 林成涛，仇斌，陈世全.电流输入电动汽车电池等效电路模型的比较[J].机械工程学报，2005，41(12)：76-81.

[11] 孙东，陈息坤，毛华夫.基于离散滑模观测器的锂电池荷电状态估计[J].中国电机工程学报，2015(1)：185-191.

[12] 盛仲飙，同晓荣.BP神经网络在曲线拟合中的应用[J].科学技术与工程，2011，1(28)：55-57.

[13] 陈光，任志良，孙海柱.最小二乘曲线拟合及Matlab实现[J].兵工自动化，2005，24(3)：107-108.

[14] SAEED S，REZA G，BOR Y L.A novel on-board state-of-charge estimation method for aged Li-ion batteries based on model adaptive extended Kalman filter[J].Journal of Power Sources，2014，245(1)：337-344.

[15] CHARKHGARD M，FARROKHI M.State-of-charge estimation for lithium-ion batteries using neural networks and EKF[J].IEEE Transactions on Industrial Electronics，2010，57(12)：4178-4187.

原创声明：此内容为AET网站原创，未经授权禁止转载。

相关内容